Inscription / Connexion Nouveau Sujet
Ressort régime forcé
Bonjour j'étudie un haut parleur modélisé par une masse M(m) se déplaçant selon l'axe (Ox)
M est accroché à l'extrémité d'un ressort de longueur à vide lo et de raideur k
Avec force de frottement fluide f=-a*v(vecteur)
Plus une force excitatrice K*i(t)*(ex) avec ex le vecteur unitaire et i(t)=Imcos(wt) :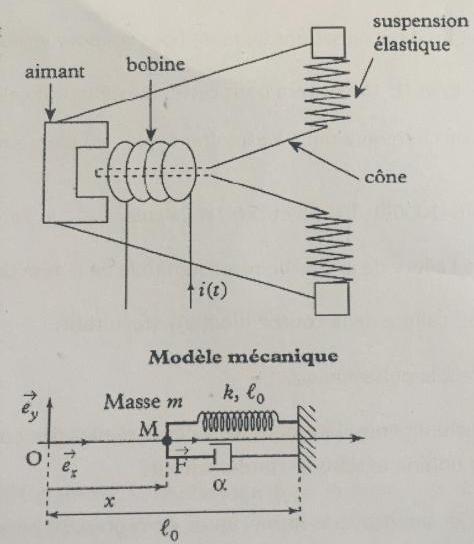
J'aimerai établir l'équation différentiel mais j'aimerai être éclairé sur le schéma. On voit que lo est la longueur entre le support et le repère mais on nous dit que c'est aussi la longueur à vide du ressort je ne comprends pas tellement
Ensuite la force de rappel ici va être positive non ? Étant donné que le vecteur unitaire est en direction du support ?
Merci à vous
Bonjour
Pour être très précis : l'origine O du repère est la position d'équilibre stable de M lorsque le ressort n'exerce aucune force (donc possède sa longueur à vide). lo désigne donc la longueur à vide du ressort si on néglige la longueur du dispositif de liaison entre la masse M et le ressort. L'essentiel à retenir :
avec ce choix de l'origine du repère, x représente exactement la variation de longueur du ressort par rapport à sa longueur à vide de sorte que la force exercée par le ressort sur la masse M peut toujours s'écrire :
quel que soit le signe de x.
Ensuite pour desuire la phase à l'origine j'ai posé en régime sinusoïdale forcé x(t)=Xcos(wt+phi)
J'aboutit a l'amplitude complexe de X égale à (K/m)*Im/(-w^2+w0/Qjw+wo^2)
J'aimerai savoir si c'est correct afin de continuer l'exercice ? Merci
Desole j'ai écris trop vite J'aboutit a l'amplitude complexe de X égale à (K/m)*Im/(-w^2+(w0/Q)jw+wo^2) de
Bonjour
Ce que tu exprimes est le complexe, qui pourrait être noté x , associé à l'élongation x(t). Pour avoir l'amplitude (valeur maximale) de l'élongation, qui peut être notée Xm, il faut prendre le module du complexe.
L'argument du complexe sera égal à la phase initiale  .
.
J'obtiens X(complexe) = Im*K/mwo^2*1/[(j((w/wo*Q)+j((w^2/wo^2)-1))]
Comment calculer l'argument de ce nombre je n'y arrive pas ca serai la somme des arguments mais je n'y arrive pas.
Pour le module j'ai Im*K/mwo^2*1/[(sqrt((w/wo*Q)^2+(w^2/wo^2)-1)^2)]
Les expressions de x précédentes étaient correctes mais ton dernier message fait intervenir un "j" en trop. De façon générale, si un complexe s'écrit x=A+j.B où A et B sont deux réels, le module vaut :
"j" n'intervient pas dans l'expression finale du module !
C'est parce que j'ai voulut factorisé par wo^2 puis par j deux fois.
Avec ce que j'avais précédemment ca donne alors Pour le module Im*K/mwo^2*1/[(sqrt((w*wo/Q)^2+(w^2-wo^2)^2)]
Mais alors trouver un argument l'expression de de X je n'y arrive pas
Enfait j'avais fait (en prenant que le dénominateur pour ne pas encrire de gros calculs ) : je met wo^2 en facteur ainsi que j
wo^2[j[jw^2/wo^2+w/Q-j]
Puis une deuxième fois j en facteur donc : wo^2[j[w/Q+j[(w^2/wo^2)-1]]
Pardon j'ai encore ecrit trop vite j'obtiens :
Enfait j'avais fait (en prenant que le dénominateur pour ne pas encrire de gros calculs ) : je met wo^2 en facteur ainsi que j
wo^2[j[jw^2/wo^2+(w/woQ)-j]
Puis une deuxième fois j en facteur donc : wo^2[j[(w/wo Q)+j[(w^2/wo^2)-1]]
Je reprends l'essentiel :
Équation différentielle :
Passage aux complexes en régime sinusoïdal forcé :
Amplitude de x(t) :
Phase initiale de x(t) sachant que celle de i(t) est choisie arbitrairement nulle :
Attention au changement de signe devant j ! La partie réelle ne gardant pas toujours le même signe, le raisonnement sur l'arctangente est délicat. Je préfère écrire que :
(signe de la partie imaginaire) donc :
Si tu veux des renseignement sur les problèmes posés par l'arctangente, tu peux regarder ici , en particulier mon message du 01-04-18 à 15:33 : ![]() Filtre Actif 2ème ordre
Filtre Actif 2ème ordre


