Inscription / Connexion Nouveau Sujet
Réfraction totale
Bonjour,
voici un exercice que j'ai du mal à comprendre :
"Exercice :
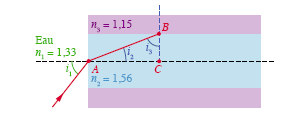
Lors d'une fibroscopie, un rayon lumineux se propageant
dans de l'eau pénètre dans une fibre optique.
1. Calculer la valeur limite de l'angle i3 à partir des
données du schéma.
2. a. Que peut-on dire du triangle ABC ?
En déduire la relation entre les angles i2 et i3.
b. En déduire la valeur de l'angle i2 lorsque i3 vaut l'angle limite.
3. Calculer la valeur de l'angle i1 lorsque i3 vaut l'angle limite.
4. Un rayon lumineux pourra-t-il se propager dans la fibre
optique quel que soit l'angle i1 ?"
Merci d'avance.
Bonsoir,
1) Il faut connaitre quelques règles que l'on appelle lois de Snell-Descartes:
1° Le rayon réfléchi appartient au plan d'incidence.
2° Il existe une relation liant l'angle d'incidence et l'angle réfléchi: i=r
3° S'il existe, le rayon réfracté appartient au plan d'incidence.
4° Il existe une relation liant les angles réfracté et incidents: n1.sin(i1)=n2.sin(i2) avec n1ou2= indice de réfraction du milieu 1ou2.
La valeur de l'angle limite pour que la lumière se propage toujours dans le coeur de la fibre optique:
On a donc au moment limite, l'angle que l'on appellera i4, angle réfracté au point B, i4=90° ce qui veut dire que le rayon lumineux arrivant en B se propage le long de la fibre optique à l'horizontal.
On applique alors la 4° loi de Snell-Descartes (je ne sais pas si ces lois ont un numéro attitré mais c'est plus pratique dans cet exercice pour comprendre de quelle formule je parle) au point B (entre les milieux 2 et 3):
n2.sin(i3)=n2.sin(i4) or on a dit i4=90° pour i3lim
n2.sin(i3lim)=n2.sin(90°)=n2
On en déduit: sin(i3lim)=n2/n1
Pour obtenir l'angle limite de i3 il faut prendre l'arcsin du calcul précédent (la touche sin-1 des calculatrices):
arcsin(sin(i3lim))=arcsin(n2/n1)
i3lim=arcsin(n2/n1)
Je te laisse faire l'application numérique... attention à l'utilisation de la calculatrice bien faire attention que ces angles sont en ° et non en rad!!!
2)a) Tu es largement capable de trouver la particularité du triangle ABC.
On sait que dans un triangle la somme des angles est égale à 180°, à toi de trouver une relation entre i2 et i3.
2)b) Pas trop compliqué à faire.
3) Utiliser la 4° loi de Snell-Descartes au point A entre les milieux 1 et 2.
On dit angle limite, l'angle qu'il faut dépasser pour avoir une réflexion totale, c'est à dire qu'au dessus de cette valeur, il y aura forcément réflexion sans réfraction. Tu dois surement le savoir mais les angles ont pour origine la normale au dioptre (droite imaginaire perpendiculaire à la surface où le rayon lumineux arrive), 90° veut dire que le rayon sera horizontal à la sortie du point B.
Si tu préfères, avant la valeur de i3limite, il y a réfraction (passe d'un milieu à un autre), en augmentant la valeur de l'angle i3 vers i3limite, le rayon réfracté se rapproche de plus en plus de la surface séparant les milieux 2 et 3, au bout d'un moment le rayon atteindra l'horizontal et c'est pour cette valeur de l'angle i3 qu'on appelle angle limite. Au delà de cette valeur, il y aura réflexion totale du rayon incident.
90° marque donc la limite entre la réfraction et la réflexion totale.
J'espère que c'est un peu plus clair mais j'en doute lol
Si tu n'as toujours pas compris, redemandes moi...


