Inscription / Connexion Nouveau Sujet
Refraction et dispesion de la lumiere
Bonjour,
J'ai besoin de votre aide pour un exercice de physique que je n'arrive pas a comprendre
Quelques éclaircissements ne seraient pas de refus 
Voici l'énoncé
Passage d'un rayon oblique a travers un cube de verre
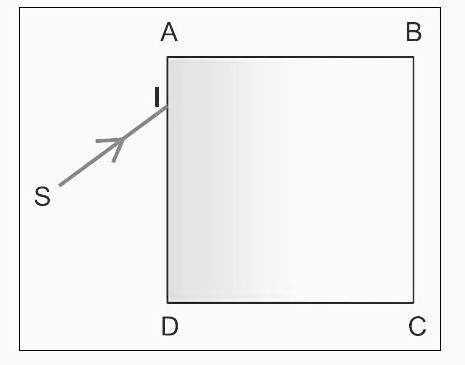
La figure représente un rayon incident SI entrant dans un cube de verre d'arête AB=a. Pour la longueur d'onde utilisée l'angle d'incidence limite vaut 39°.
1) Quel est l'indice de réfraction 'absolu' du verre ? (nous n'avons pas mentionné la notion 'd'indice de réfraction absolu' en cours, les définitions trouvées sur internet sont complexes)
2) On a IA = a/5. Établir la condition à laquelle doit satisfaire l'angle i pour que le rayon réfracte$é dans le verre arrive sur AB
3) Cette condition étant réalisée, construire le trajet suivi par la lumière si i=45°, si i=90°. Exprimer la déviation subie par le rayon
Merci d'avance pour votre aide
Bonjour,
Tu dois savoir qu'un milieu dispersif, c'est un milieu dont l'indice dépend de la longueur d'onde de la radiation le traversant... C'est pour cela qu'un prisme ou une goutte d'eau, par exemple, décompose la lumière blanche.
Donc à chaque radiation, on peut associer une valeur d'indice, dit "relatif".
Si maintenant, on considère que c'est la même valeur d'indice pour toutes les radiations, on utilisera le terme d' "absolu".
Contente toi de retenir que c'est l'indice du milieu tel qu'on a l'habitude de te le donner dans les exos (n = ...)
Q1) Indice du verre
La question est vicieuse ! On te parle de rayon (SI) dans l'air, je suppose, et entrant dans le cube en verre.
L'angle limite d'incidence, c'est la valeur de l'angle pour laquelle on est à la limite de la réflexion totale, c'est-à-dire que l'angle de réfraction vaut r = 90°.
Donc c'est lorsqu'un rayon de lumière passe du VERRE dans l'air !!!
(Oubli de ton prof, véritable piège ou n'aura-t-il pas réfléchi à son exo ???  )
)
Il faut donc utiliser la seconde loi de Snell-Descartes : n1.sin(i) = n2.sin(r) avec n1 = n(verre) et n2 = n(air)
sinon le calcul n'est pas possible !
n(verre)  sin(39°) = 1,00
sin(39°) = 1,00  sin(90°)
sin(90°)
C'est-à-dire : n(verre) = 1,00  1/0,63
1/0,63  1,58
1,58
Q2) Condition d'arrivage sur [AB]
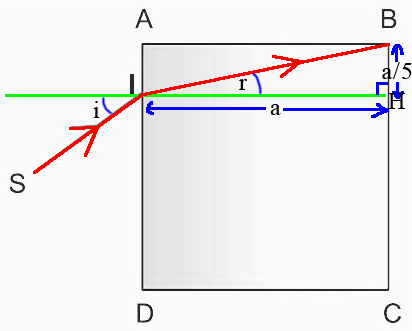
Comme tu peux le voir sur ma figure, je t'ai tracé la normale en vert et je t'ai indiqué les angles i et r ainsi que les longueurs connues.
Tu remarques bien que si r était plus petit, le rayon ne frapperait pas [AB]. Dans le cas limite, le rayon vient frapper en B.
Dans cette configuration, tu as donc un triangle (IBH) rectangle en H, de côté (a/5) et (a).
Par trigonométrie :
tan(r) = c.opposé/c.adjacent = (a/5) / (a) = 1/5 d'où r = arctan(1/5) = tan-1(1/5)  11,31°
11,31°
L'angle de réfraction doit être plus grand que 11,31° !
Loi de Snell-Descartes appliquée au point I:
n(air) sin(i) = 1,58
sin(i) = 1,58 sin(11,31) donc que i = 18,05°.
sin(11,31) donc que i = 18,05°.
Il faut donc que l'angle d'incidence i soit compris entre 18,05° et 90° pour que r  11,31°
11,31°
Comment puis-je affirmer cela ?
Supposons que i = 5° < 18,05°, dans ce cas, r vaudrait par la loi de Descartes, 3,1° ce qui est contraire à ce que l'on veut !
D'ailleurs, c'est pour ça que la question 3 te demande de tracer pour i = 45° et i = 90° (donc supérieurs à 18,05°)
Je te laisse calculer les valeurs de r et tracer les chemins des rayons pour la fin !