Inscription / Connexion Nouveau Sujet
Réalisation d'une régression linéaire pour Boyle-Mariotte
Bonjour,
Je "bloque" sur un TP à propos de la loi de Boyle-Mariotte :
On nous a donné un tableau indiquant les résultats d'une expérience qui consistait à enfermer une quantité d'air atmosphérique dans une seringue pour décrire son comportement lorsque le volume qui lui est offert est plus ou moins grand.
Le voici :
Numéro de la mesure 1 2 3 4 5 6
P(hPa) 253 304 380 506 759 1012
V(cm3) 60 50 40 30 20 15
Or question 2, il m'est demandé de représenter graphiquement l'évolution de la pression en fonction du volume, et de voir à quelle sorte de fonction elle ressemble (fonction inverse je crois)
Puis question 4, il faut proposer une nouvelle représentation graphique permettant la réalisation d'une régression linéaire des résultats expérimentaux.
Et là... je ne vois vraiment pas... grâce à ce cher google j'ai presque compris ce qu'était une régression linéaire, mais sinon... bref je ne vois pas...
merci d'avance 
Bonjour,
Question 2
As-tu tracé le graphique représentant les valeurs de P en fonction de celles de V ?
Oui, cela semble bien être une fonction inverse. Mais comment en être sûr ?
Comment écrirais-tu, par une relation mathématique, cette fonction, si c'est bien une fonction inverse ?
Question 4
Tu sais ce qu'est une fonction linéaire (programme de troisième au collège)
y = a x
Comment modifier l'écriture de la relation trouvée à la question 2 pour que P soit une fonction linéaire d'une fonction de V
Pas clair ?
On cherche à écrire P = a Z
Et qu'est-ce que Z ? c'est une fonction de V
Pourquoi faire cela ?
Parce qu'il n'est pas simple d'être sûr qu'une fonction est une fonction inverse (comme tu le penses à la deuxième question)
Alors qu'il est beaucoup plus simple de vérifier qu'une fonction est une fonction linéaire.
Que proposes-tu ?

A la question 2, je pense que tu peux tracer un graphique qui ressemble à celui de gauche :
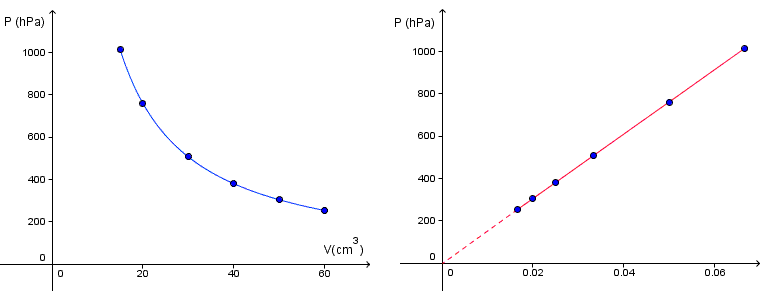
Et à la question 4, tu cherches à tracer un nouveau graphique, comme celui de droite...

Merci beaucoup ! C'est surtout le terme de "régression linéaire" qui m'embêtait.
Et donc normalement on peut faire soit le Volume en fonction de l'inverse de la Pression, soit la Pression en fonction de l'inverse du Volume, non ?
Et l'équation de la courbe de la question 4 donne
y=mx où y=Volume et X=1/Presion
Et donc m est la constante dont parle la loi de Boyle-Mariotte ? merci encore en tous cas ^^
Puisque l'énoncé dit "la pression en fonction du volume", c'est la pression en ordonnées et le volume en abscisses (comme sur mon graphique de gauche).
Et l'hypothèse que l'on fait est que la loi est probablement
Pour le vérifier, la manière la plus simple consiste à essayer de voir si P en fonction de est une fonction linéaire puisque
peut s'écrire



