Inscription / Connexion Nouveau Sujet
RDM poutre en flexion
Bonjour,
Je rencontre des problèmes pour établir l'expression du torseur de cohésion sur un exercice de rdm ... Je pense que la méthode n'est pas bien claire pour moi.
Il s'agit d'une poutre encastrée, soumise à son poids (qui n'est pas représenté sur le croquis), et retenue à une distance (L-l) par un câble, modélisé sur le schéma par une force Fa.
Mon problème se situe majoritairement dans l'expression des moments du torseur de cohésion.
Merci d'avance pour vos conseils.
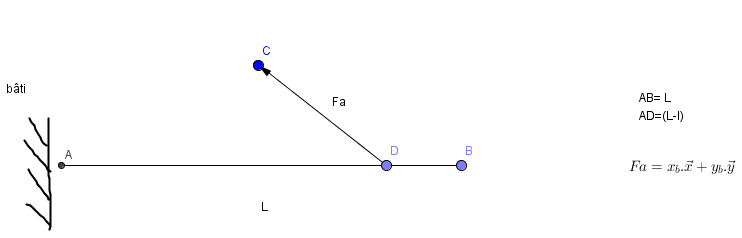
Ce que j'ai déjà fait :
Utiliser le principe fondamental de la dynamique pour établir l'expression de la résultante du torseur de cohésion :
Salut,
Tu as deux découpages fictifs à faire pour le moment :
x appartient à [DB] et x appartient à [AD].
J'avais explique à un membre récemment une méthode intuitive pour déterminer un moment fléchissant dans le cas d'une charge répartie :
![]() Rdm charge triangulaire décroissante
Rdm charge triangulaire décroissante
Essaie de me faire une proposition ensuite 
Bonsoir !
Je me suis replongé dans les calculs ce matin, cela m'à semblé plus simple à tête reposée !
Sur le segment AD, je trouve l'expression du torseur de cohésion :
xB 0
Yb+P(L-l-x) 0
0 P/2*(L-l-x)²+Yb(L-l-x) (Désolé pour la mise en forme)
Et sur le segment DB :
0 0
P(L-x) 0
0 P(L-x)²/2
J'en suis là. Merci d'avoir répondu et merci pour l'aide !
Bonne soirée 
Alors si on décompose
sur [AD]
N(x) = -Xb --> attention au sens du repère
Ty = Yb - P.(L-l-x) --> idem
Mfz = -P/2*(L-l-x)² + Yb(L-l-x) --> idem
sur [DB]
N(x) = 0
Ty = - P.(L-x) --> attention au sens du repère
Mfz = -P/2*(L-x)² --> idem

Bonsoir !
Ayant posé le problème seul (il n'est pas tiré d'un énoncé), j'ai prit la liberté d'intégrer les signes dans les expressions Xb et P, que j'ai posé au début du problème !
J'ai en effet oublié de le mentionner dans mon message et je m'en excuse, la remarque en est donc très pertinente !
Merci beaucoup pour les conseils et la superbe méthode décrite dans l'autre discution ! elle me resservira sûrement ! 



