Inscription / Connexion Nouveau Sujet
Rdm charge triangulaire décroissante
Bonjour,
je cherche mais je ne vois pas mon erreur...
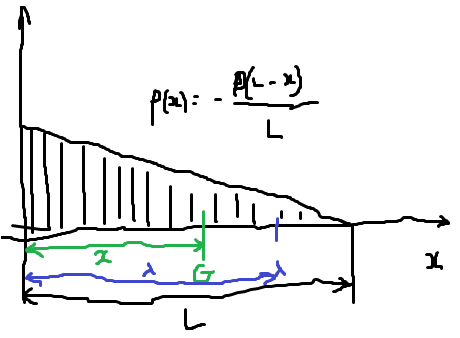
Une poutre console de longueur L avec une charge triangulaire décroissante, je cherche le moment fléchissant.
Une coupure en G et je fais le calcul, je prends à droite comment ça je n'ai pas les réactions à calculer. j'ai ma charge répartie p(x)=-P(L-x)/L en M de distance par rapport à l'origine que j'intègre entre G (distance x depuis l'origine) et L:
Jusque là c'est bon?
Après j'intègre et je trouve:
or dans les bouquins, je trouve:
J'ai refait les calculs plusieurs fois, impossible de trouver l'erreur, pouvez-vous me débloquer?
Bonne journée
Salut,
Pourrais-tu faire un schéma de la situation stp x) ?
Ce serait plus clair (sur paint par exemple).
Je ne l'ai pas retrouvé, je vais donc te proposer une méthode alternative sans calculs d'intégrales :
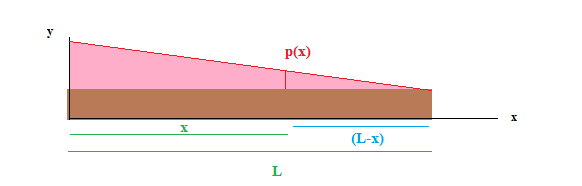
Soit une charge répartie telle que :
(selon
)
p(L) = 0
donc à une abscisse x, d'après le théorème de Thalès, on a :
Je cherche donc le torseur de cohésion en G, pour rappel, à cette abscisse x,
"+" ce qui est à droite,
"-" ce qui est à gauche
donc en regardant uniquement les efforts à droite, l'effort tranchant est tout simplement l'aire du triangle des efforts à droite de G :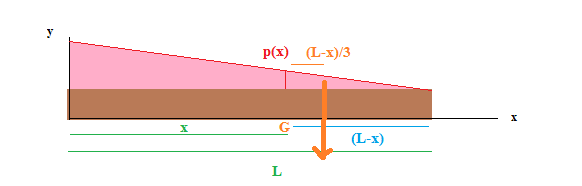
(base x hauteur / 2)
puis le moment fléchissant s'écrit tout simplement : (bras de levier x effort)
saur erreur d'inattention
Ok ! merci pour ta réponse. tu trouves donc la résultante avec l'aire du triangle, tu en déduis qu'elle se place à 1/3 de la longueur considérée et tu fais le bras de levier, c'est bien ça?
Mais si j'intègre p(x) le long de la poutre pourquoi je n'obtiens pas le résultat?
en faisant avec lambda la distance OM?
Le moment vectoriellement c'est bien la distance la force (quand le moment au point considéré est nul)
C'est bien ça .
Ce doit être une petite erreur d'intégration je pense, il faudrait que je la refasse.
Il n'empêche que ma méthode n'est pas mal non 
?
Oui ! c'est clair !Merci ! 
mais je pensais avoir trouvé une manière de faire qui marche à tous les coups sans trop réfléchir.
A l'occaz, si tu peux me dire où je me suis planté sur l'intégration... parce que là, je sèche.
Et disons que c'est ma manière de procéder alors s'il y a une faille, je veux la trouver 
Bonjour,
C'est effectivement une erreur d'intégration : quand tu intègres x au carré tu obtiens x au cube divisé par 3 => d'où le facteur 6.
(je n'ai pas encore compris comment utiliser le code pour faire des belles formules).
J'avais la flemme de recalculer en tout cas merci pour la formule (la bonne) !
Zeppo
Annuler
connectez vous