Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... AutreForum autre de supérieur PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie

1 2 +

Posté par
gbm Webmasterre : RDM - Flexion 26-03-20 à 17:41

Un peu de bon sens physique, fais le tests avec une règle en métal si tu ne le sens pas :

RDM - Flexion

Posté par
lidlkidjoere : RDM - Flexion 26-03-20 à 17:42

Ps : H/2 existe de 0 à L

Posté par
gbm Webmasterre : RDM - Flexion 26-03-20 à 17:43

Post-croisés

Oui, on se place désormais à x = L/2 grâce à l'étude de la fonction

Maintenant on regarde l'évolution de la contrainte en fonction de la cote y :

RDM - Flexion

Posté par
ShowTaKere : RDM - Flexion 26-03-20 à 17:49

Oui cela dépend de y. On aurait donc un diagramme de contrainte, mais je ne vois pas lequel car cela dépend si Mfmax >0 ou <0 d'après ce qui est cités dans le pdf.

Posté par
lidlkidjoere : RDM - Flexion 26-03-20 à 17:53

Certes, tu pourrais avoir un treuille qui tire sur la poutre avec cette dernière fixée en A et B

Posté par
gbm Webmasterre : RDM - Flexion 26-03-20 à 19:02

ShowTaKe @ 26-03-2020 à 17:49

Oui cela dépend de y. On aurait donc un diagramme de contrainte, mais je ne vois pas lequel car cela dépend si Mfmax >0 ou <0 d'après ce qui est cités dans le pdf.


Je te rappelle qu'on a déterminé que Mfz est maximal et positif en x = L/2, cf. le diagramme.

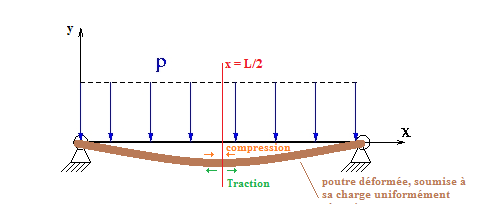
Eu égard à la cote y, la contrainte sera - au signe près - maximale en extrémité de section :
- en y = +h/2, pour laquelle il y aura une compression maximale ;
- en y = -h/2, pour laquelle il y aura une traction maximale.

Posté par
ShowTaKere : RDM - Flexion 26-03-20 à 19:16

Ah je comprend mieux. Merci beaucoup pour votre aide sur ces différentes questions. Cependant dans la question 2 concernant la simplification auriez vous une piste à le donner pour y répondre ?

Encore merci.

Posté par
gbm Webmasterre : RDM - Flexion 26-03-20 à 19:29

Je t'en prie mais révise tout ça car la méthode faite ensemble devra être maîtrisée sur le bout des doigts.

Tu trouves quoi du coup pour les deux contraintes ?

Concernant la question 2, j'ai du mal à comprendre en quoi cela simplifierait les deux expressions trouvées : plutôt que d'avoir une charge \vec{p} répartie, on a une masse m = masse volumique x volume soumise à l'accélération de la pesanteur \vec{g} uniformément répartie ...

Posté par
ShowTaKere : RDM - Flexion 26-03-20 à 19:45

Que voulez vous dire par « Tu trouve quoi pour les deux contrainte ? ». Vous souhaitez que je remplace y par h/2 et -h/2 dans la formule, où alors je n'ai pas saisi.

Je vais cependant arrêter un peu là pour cette journée car je suis fatigué. Je vous souhaite une bonne soirée et un bon repos.

Merci à vous

Posté par
gbm Webmasterre : RDM - Flexion 26-03-20 à 20:05

Oui c'est ce que je souhaite.

Ensuite, il ne faudra pas oublier de remplacer le moment quadratique I par sa valeur.

Ça marche, bonne soirée !

Posté par
ShowTaKere : RDM - Flexion 27-03-20 à 08:22

Bonjour,

Du coup on prend la formule pour f(L/2) = -pL²y/8I
En remplaçant avec y=h/2 et I=bh³/12 on obtient : -pL²h/16I
=-pL²h/16*(b*h³/12)
=-pL²/16*b*h²/12

En remplaçant avec y=-h/2 et I=bh³/12 on obtient : pL²h/16I
=pL²h/16*(b*h³/12)
=pL²/16*b*h²/12

Posté par
gbm Webmasterre : RDM - Flexion 27-03-20 à 09:54

Bonjour,

OK, je te fais confiance pour ces dernières expressions.

Pour la question 2, à part refaire en considérant que la charge répartie vaut

p(x) = m(x) \times g = \gamma \times V(x) \times g

V(x) étant la portion du volume de poutre considérée à l'abscisse x et g l'intensité de la pensanteur, je ne vois pas ...

Posté par
ShowTaKere : RDM - Flexion 27-03-20 à 11:07

D'accord d'accord. Après si vous ne voyez pas c'est pas grave, j'essaierai de voir peut être de mon côté comment je peux faire.

Je vous remercie en tout cas pour votre patience et l'aide que vous m'aurez apportés durant ces 3 jours

Posté par
gbm Webmasterre : RDM - Flexion 27-03-20 à 11:16

Je t'en prie, essaie de voir ce que ma proposition donne (9h54), en se souvenant qu'à une coupure de la poutre (abscisse x), on regarde soit les efforts (donc ici le poids propre et la réaction d'appui) à droite, soit à gauche, au signe près.

En espérant que tu te sens plus à l'aise avec les notions fondamentales du cours et les méthodes à appliquer

Posté par
ShowTaKere : RDM - Flexion 27-03-20 à 11:26

Oui j'ai mieux compris comment la méthode et comment l'appliquer.
La formule de la contrainte est : (-p(L-x)² +pL(L-x)*6y)/b*h³
Mais je ne comprend pas bien ce que vous souhaitez faire.

gbm @ 27-03-2020 à 09:54

Bonjour,

OK, je te fais confiance pour ces dernières expressions.

Pour la question 2, à part refaire en considérant que la charge répartie vaut

p(x) = m(x) \times g = \gamma \times V(x) \times g

V(x) étant la portion du volume de poutre considérée à l'abscisse x et g l'intensité de la pensanteur, je ne vois pas ...

Posté par
gbm Webmasterre : RDM - Flexion 27-03-20 à 12:32

Tu remplaces p(x) dans la relation trouvée pour la contrainte

Il reste à définir V(x) pour la portion de circuit étudiée ...

Posté par
ShowTaKere : RDM - Flexion 27-03-20 à 13:47

Si j'ai bien compris j'ai remplacer p(x) par \gamma*V(x)*g

Du coup on obtient : -(\gamma*V(L-x)²+L*\gamma*V(L-x)*6y/b*h³

Si c'est cela dont vous souhaitez, mais je ne vois pas où cela va nous amener.

Posté par
gbm Webmasterre : RDM - Flexion 27-03-20 à 14:25

Si tu regardes la coupure à droite, tu as effectivement un volume de poutre V(L-x), ce qui est le volume d'un parallélépipède de longueur (L-x), de hauteur h et de largeur b ...

Cela pourrait simplifier l'expression que tu as rappelée ci-dessus

Posté par
ShowTaKere : RDM - Flexion 27-03-20 à 15:09

Pourriez-vous me montrer la simplification je n'arrive pas a la voir. Je vois parfaitement l'idée du volume du parallélépipède mais je ne vois comment simplifier.

Posté par
gbm Webmasterre : RDM - Flexion 27-03-20 à 16:42

Comme j'avais pu te l'écrire, je ne suis pas moi-même convaincu par la simplification :

\sigma _{xx} = \dfrac{p.y}{2I}.x² - \dfrac{p.L.y}{2I}.x

avec p(x) = m(x) \times g = \gamma \times V(x) \times g = \gamma . x . h . b . g

\sigma _{xx} = \dfrac{p.y}{2I}.(x² - L.x)

\Leftrightarrow \sigma _{xx} = \dfrac{ \gamma . x . h . b . g . y}{2 \frac{b.h^3}{12}}.(x² - L.x)

\Leftrightarrow \sigma _{xx} = \dfrac{ 6 \gamma . x . h . b . g . y}{b.h^3}.(x² - L.x)

\Leftrightarrow \sigma _{xx} = \dfrac{ 6 \gamma . g . y}{h^2}.(x^3 - L.x^2)

Si on prend par exemple la cote y = \dfrac{h}{2} on aurait :

\Leftrightarrow \sigma _{xx} = \dfrac{ 3 \gamma . g }{h}.(x^3 - L.x^2)

et si y =- \dfrac{h}{2}

alors on aurait :

\Leftrightarrow \sigma _{xx} = - \dfrac{ 3 \gamma . g }{h}.(x^3 - L.x^2)

Après on peut donner les expressions pour x = \dfrac{L}{2} ...

Sauf incompréhension de l'énoncé ou erreur d'inattention

Posté par
ShowTaKere : RDM - Flexion 27-03-20 à 17:00

Merci beaucoup de l'aide

Si x=L/2 on obtiendrait : \frac{-3.\gamma.g }{h}.\frac{-L³}{8}

Un grand merci à vous en tout cas pour l'aide que vous m'avez apporté.

Posté par
gbm Webmasterre : RDM - Flexion 27-03-20 à 17:20

Si on prend par exemple la cote y = \dfrac{h}{2} on aurait :

\Leftrightarrow \sigma _{xx}(\dfrac{L}{2}) = \dfrac{ 3 \gamma . g }{h}.(\dfrac{L^3}{8} - \dfrac{L^3}{4}) = - \dfrac{ 3 \gamma . g. L^3 }{8h}

et si y =- \dfrac{h}{2}

alors on aurait :

\Leftrightarrow \sigma _{xx} (\dfrac{L}{2}) = = + \dfrac{ 3 \gamma . g. L^3 }{8h}

Peut-être que ça simplifie un peu l'expression en fait

Posté par
ShowTaKere : RDM - Flexion 27-03-20 à 17:21

gbm @ 27-03-2020 à 17:20

Si on prend par exemple la cote y = \dfrac{h}{2} on aurait :

\Leftrightarrow \sigma _{xx}(\dfrac{L}{2}) = \dfrac{ 3 \gamma . g }{h}.(\dfrac{L^3}{8} - \dfrac{L^3}{4}) = -  \dfrac{ 3 \gamma . g. L^3 }{8h}

et si y =- \dfrac{h}{2}

alors on aurait :

\Leftrightarrow \sigma _{xx} (\dfrac{L}{2})  = = + \dfrac{ 3 \gamma . g. L^3 }{8h}

Peut-être que ça simplifie un peu l'expression en fait


Oui un peu ahah Un grand merci à vous votre patience et le temps que vous m'avez accordé

Posté par
gbm Webmasterre : RDM - Flexion 27-03-20 à 18:10

Je t'en prie ! Refais quand même une passe sur tout ce qu'on a fait pour éviter une faute d'inattention.

J'espère que tu auras mieux appréhendé la RDM et reviens-nous avec de bonnes nouvelles

Posté par
ShowTaKere : RDM - Flexion 28-03-20 à 09:08

Oui pas de soucis. Par contre, j'aurai une question a traiter sur un autre exercice. Mais j'ai peur que d'ouvrir un nouveau topic serait inutile puis-je la poser ici ?

Posté par
gbm Webmasterre : RDM - Flexion 28-03-20 à 09:32

Bonjour,

1 sujet posté = 1 exercice = 1 question

Il n'y a pas de sujet inutile à créer

1 2 +


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !