Inscription / Connexion Nouveau Sujet
RDM - Determination de T, M et N
Bonjour à tous,
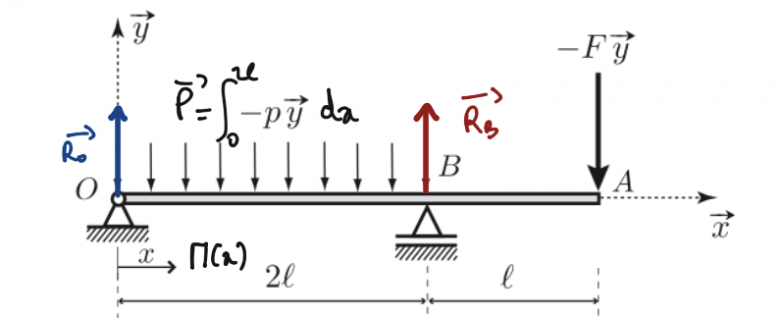
J'ai essayé de résoudre l'exercice suivant : la question demande de déterminer le moment M, l'effort tranchant T et N le long de la poutre (image ). J'ai utilisé la méthode des coupures mais je ne suis pas du tout sûre de mes résultats qui me semblent bizarres et je ne sais pas comment les vérifier...
Je trouve les résultats suivants :
0 <x<2l:
T1 = pl - F/2
N1 = 0
M1 = (F/2)*x
2l<x<3l:
T2 = F
N2=0
M2 = F(3l-x)
Avec Ro = pl - F/2 ; Rb = pl + 3F/2
Merci d'avance si quelqu'un peut me faire un retour!
Bonjour,
La prochaine fois, n'hésite pas à détailler étape par étape ton raisonnement, ça nous fait gagner du temps.
1) Détermination des efforts aux appuis :
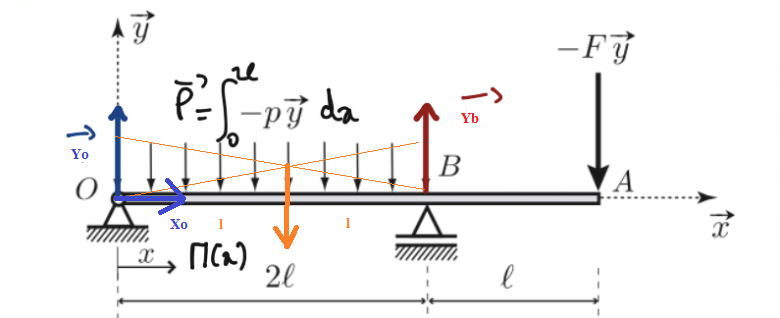
(1) : Equation de la résultante statique / x :
(2) : Equation de la résustante statique /y :
(3) : Equation de moment en B par rapport à z :
(3)
(3)
(3) dans (2)
2) Détermination du torseur de cohésion :
entre B et A : "+" ce qui est à droite
entre O et B : "-" ce qui est à gauche

Bonjour et merci pour votre réponse!
En essayant de le refaire, je n'arrive pas à avoir le bon raisonnement pour trouver vos résultats. Pourriez vous m'aider sur ces deux points?
Les deux questions concernent l'intervalle [2l,3l]
Si j'utilise la résultantes des forces selon Ty :
T - F = 0 => T = F alors que vous trouvez T = -F
Pour le moment fléchissant sur z, j'ai :
Mz - BA^F = 0
Avec BA = L
J'obtiens alors Mz = FL
Pourquoi utiliser BA = (3l -x) ? J'ai beaucoup de mal à comprendre quand utiliser x et quand utiliser la valeur L
Merci d'avance !
Souviens-toi que dans ton cours tu as la relation suivante : , ça peut aider pour vérifier les signes
 .
.
Ensuite, j'ai expliqué la notion de coupure avec la gestion du signe dans le torseur de cohésion ici : ![]() RDM - Flexion
RDM - Flexion
Regarde ce sujet attentivement, tu devrais comprendre ton erreur.
Merci! J'ai maintenant bien compris comment utiliser les signes.
J'ai toujours une question cependant, je ne comprends pas comment exprimer mon vecteur OM dans les deux intervalles.
Dans le deuxième intervalle il me semble que vous aillez AB = 3L - x ?
Oui c'est bien que ce j'ai écrit :
entre B et A : "+" ce qui est à droite
x entre B et A si tu préfères

Regarde le repère défini : son origine est en O.
Donc si x  [BA] alors 2l
[BA] alors 2l  x
x  3l et si je regarde à droite de la coupure (abscisse x), alors j'ai un bras de levier de (3l - x).
3l et si je regarde à droite de la coupure (abscisse x), alors j'ai un bras de levier de (3l - x).
Autre vérification, si Mfz = -F.l comme tu l'écris, alors Ty = - dMfz/dx = 0, ce qui n'est pas vrai

Pas vraiment ^^
Je sais bien que c'est la bonne réponse, et j'ai regardé la méthode du bras de levier mais de ce que j'ai compris cela correspond à la distance entre la force et le point d'application, donc je prendrais AB = L en premier instinct, ce qui n'est pas bon...
Y a t il une « méthode » sur laquelle je pourrais m'appuyer?
Désolée du dérangement et merci pour votre implication !
Bonjour,
Là je n'ai qu'une chose à écrire : c'est qu'il faut que tu révises la notion de moment d'une force en un point, suivant un axe donné.
Etant donné que mon repère a pour origine O, c'est l'origine des abscisse, donc si je prends une coupure entre B et A, l'abscisse x sera bien entre 2l et 3l, et si je regarde les efforts à droite de la coupure, le bras de levier sera bien (3l - x).

Bonjour,
Peut-être que ce schéma t'aidera à illustrer mes propos : 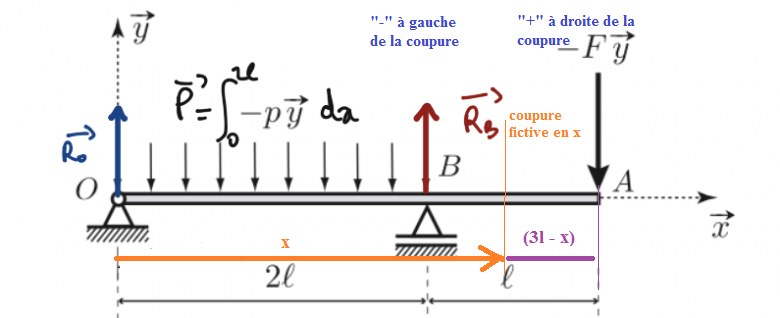
Si je regarde à droite de la coupure d'abscisse x :
Mfz = "effort" x "bras de levier"
Mfz = -F.(3l - x)
Je t'en prie, à une prochaine fois !
PS : c'était bon pour la rotation sur l'autre exercice ?
Merci pour le schéma! Dans ma tête j'effectuais la coupure au point B et je ne comprenais donc pas l'utilisation de x mais c'est plus clair maintenant !
Et oui c'était bon pour la rotation ! 


