Inscription / Connexion Nouveau Sujet
rayon incident, réfracté et réfléchi
Bonjour, voici un exercice de physique où j'ai répondu à la question 1, 2 et 5 mais je n'y arrive pas pour la 3 et la 4, pourriez-vous me dire si mes réponses sont justes et m'aider pour les questions 3 et 4, s'il-vous-plaît?
Exercice:
Données : indice de l'air : n0 = 1,0 ; indice du verre : n = 1,5.
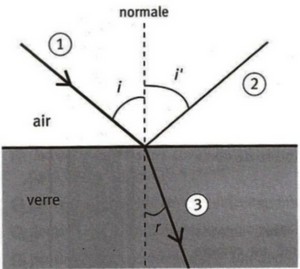
1. Identifier sur le schéma suivant (voir image n°1) le rayon incident, le rayon réfracté, le rayon réfléchi.
- J'ai mis en n°1: rayon incident / n°2: rayon réfléchi / n°3 : rayon réfracté.
2. Le rayon réfracté est-il dans le plan formé par le rayon indicent et la normale?
- J'ai mis « oui » car d'après la loi de Snell Descartes : le rayon incident et le rayon réfracté sont dans le même plan: le plan d'incidence. Ce plan d'incidence contient le rayon incident et la normale au point d'incidence. "ou" Le rayon réfracté se situe dans le plan d'incidence (défini par le rayon incident et la normale au dioptre au mouvement d'incidence), rayon incident et rayon réfracté étant de part et d'autre de la normale.
3. Exprimer sinr en fonction de n0,n sini calculer l'angle r. Donnée : i = 55°.
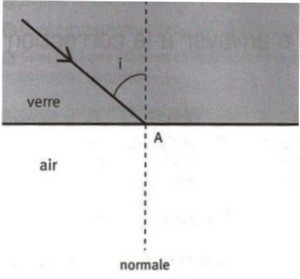
4.Le rayon lumineux incident est maintenant situé dans le verre avec i = 55°.
Observera-t-on le phénomène de réflexion totale? Justifiez la réponse de manière précise.
Tracer le " trajet " du rayon lumineux après le point A. (voir image n°2)
5. Citer une application de la réfection totale en médecine.
J'ai mis: La fibroscopie est une application de la réflexion totale en médecine qui est un examen médical permettant de visualiser l'intérieur du corps.
Merci d'avance  Bubulle-13
Bubulle-13
Bonjour,
Oui pour les réponses aux questions 1, 2 et 5
Question 3 :
Tu connais la loi de Snell-Descartes
Quelle est la relation entre mesures des angles et indices des milieux qui accompagne cette loi ?
Peux-tu écrire cette relation et bien identifier les quatre variables de cette relation ?

Dac' merci, je peux déjà recopier les réponses 1, 2 et 5 pour les autres, je vais essayer de trouver.
Merci 
Je connais la deuxième loi de Snell Descartes qui dit:
- L'angle d'incidence i1 et l'angle de réfraction i2 (angle entre la normale et le rayon réfracté) sont liés par la relation : n1 sin i1 = n2 sin i2.
- La loi de Descartes permet décrire:
nverre sin i2 = nair sin i1,  nverre = sin i1 / sin i2.
nverre = sin i1 / sin i2.
Sur le schéma, nous lisons: angle d'incidence i1 = 60° ; angle de réfraction: i2 = 35°.
nverre = sin(60) / sin(35) soit: nverre = 1,5.
Oui avec cette ligne :
- L'angle d'incidence i1 et l'angle de réfraction i2 (angle entre la normale et le rayon réfracté) sont liés par la relation : n1 sin i1 = n2 sin i2.
On va appliquer cette relation à deux reprises.
1) Pour la question 3
Le milieu "1" est l'air, donc :
n1 = 1,0
i1 = 55°
Le milieu "2" est le verre, donc :
n2 = 1,50
i2 est l'angle de réfraction qu'il faut calculer
2) Pour la question 4
Le milieu "1" est le verre, donc :
n1 = 1,50
i1 = 55°
Le milieu "2" est l'air, donc :
n2 = 1,0
i2 est l'angle de réfraction qu'il faut calculer (en faisant bien attention !)
A toi !



