Sans énoncé, il n'y a pas d'aide possible.

Je te déconseille de publier ton énoncé sous forme de photo.
C'est interdit par le règlement ( Sauf les schémas et tableaux ) et un modérateur ne tarderait pas à le supprimer.

La solution consiste à le recopier.

Ah mince mais du coup comme la photo ne c'est pas afficher je pense que il n'y a pas de problème du coup ?

Voici l'énoncé
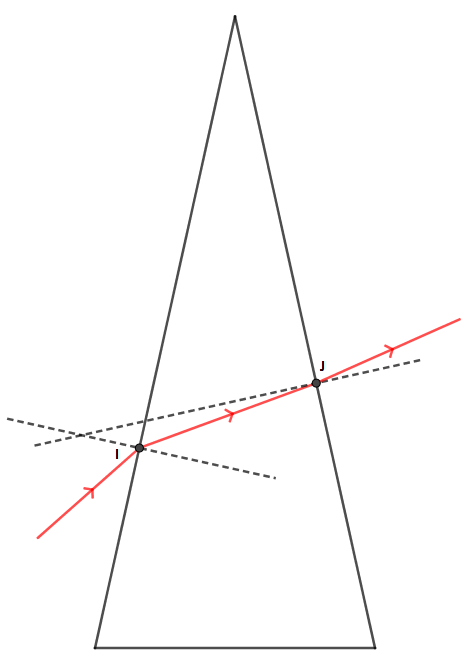
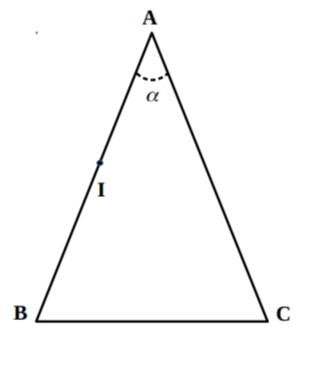
On considère un prisme d'angle au sommet A:  a=25°. Un rayon de lumière arrive au point I sur la face AB avec un angle i1=36° colle représenté

1.Calculer l'angle i2 d'incidence de ce rayon
2. Quel est l'angle de réfraction i3 avec lequel le rayon de lumière entre dans le prisme ?
Ce rayon atteint alors la face AC au pont J
3.Calculer l'angle d'incidence i4 de ce rayon au point J
4.En déduire l'angle i5 avec lequel le rayon lumineux sort du prisme.
5.Calculer l'angle it total de déviation du rayon entre son entrée dans le prime et sa sortie.

Il ne te reste plus qu'à publier la figure (sans le texte) pour rendre ton énoncé compréhensible.

Voilà la figure

L'énoncé dit :
"Un rayon de lumière arrive au point I sur la face AB avec un angle i1=36° colle représenté "
Mais la figure ne montre pas l'angle i₁

Merci de publier une figure complète, parfaitement identique à celle de l'énoncé.

Oui mais je l'ai pas inventer la figure c'est celle de l'exercice donc c'est la seule figure que je peux donner .

Et ....
Complète ton énoncé en donnant l'indice de la matière dont est fait le prisme.

Normalement je n'ai rien à compléter ce n'est pas ma faute j'ai simplement recopier la totalité de l'énoncé si ce n'est pas indiquer c'est que cest logique, un prisme est en verre ou en plexiglas et pour compléter ils ont pour indice de réfraction tout deux 1,50

Il y a écrit " un angle i₁ comme représenté "
Je n'ai pas vu de représentation de l'angle i₁.

Certes, un prisme est souvent en verre ou en plexiglas
Suivant la nature des différentes sortes de verre l'indice est compris entre 1,45 et 1,65
Je n'ai aucune raison de privilégier un indice de 1,50
Pour les différentes matières plastiques transparentes ( plexiglas, polycarbonate, polypropylène etc .... ) même incertitude.

Bref, je m'estime insuffisamment informé pour pouvoir t'aider efficacement et je passe bien volontiers le relais à quelqu'un de plus futé que moi.

Oui pour ça je suis d'accord avec vous la personne ayant fait l'énoncé ne l'a pas compléter mais ce n'est pas moi qui n'ai pas compléter l'énoncé vous me dites de rajouter quelque chose que je n'ai pas et pour l'indice mon professeur m'a appris que c'était de 1,50 on a du mal m'informer je n'étais pas au courant qu'il était compris entre deux valeurs .

Je suis désolé et je te demande de m'excuser pour t'avoir attribué à tort les insuffisances de l'énoncé.

J'ai été induit en erreur par de très nombreux cas ou les demandeurs d'aide publient des énoncés incomplet pour s'épargner la peine de tout recopier.

C'est pas grave je comprend

Tu trouveras ici (paragraphe 1.2)     les éléments nécessaires pour terminer ton exercice.

Mercii beaucoup

Voilà ce que  j'ai trouver pour la question 3 mais je pense qu'il y a un problème colle je trouve une valeur négative

3. A=i3 + i4          i3=32,6°     i4=?      A=25°
25=32,6 + ?
?= 25-32,6 = (-7,6)
i4=(-7,6)

L'angle i₄ a bien une valeur absolue de 7°6.
Selon qu'il est situé d'un côté ou de l'autre de la normale il est positif ou négatif.
Les conventions de signe sont expliquées sur le site que je t'ai indiqué (paragraphe 1.2)

Je suis aler voir donc si je comprend bien ici  i2 et i3 sont toujours positifs dû à leur orientation dans le sens trigonométrique et i4 et i5 sont toujours négatifs comme ils ont une orientation dans le sens  de l'aiguille d'une montre.
Mais donc je note que l'angle i4 est égal à -7,6 ° et non 7,6°?

Effectivement, dans le cas de cet exercice tu as bien i₂ et i₃ >0 et i₄ et i₅ <0
C'est l'adverbe " toujours " qui me tracasse.
Dans d'autres cas les signes ne seront pas forcément les mêmes.

Le mieux est de dire que la mesure de i4 est égale à 7,6° et que sa valeur algébrique est de -7,6°

En revanche pour les calculs ultérieurs, conserver la valeur algébrique.

Merci énormément de votre réponse j'ai enfin compris grâce à vous encore merci !