Inscription / Connexion Nouveau Sujet
Principe du réfractomètre de Pulfrich
J'ai un exercice de physique sur le Principe du réfractomètre de Pulfrich, et j'aimerais qu'on m'aide un peu. :/
J'espère que vous pourrez... Merci d'avance!
Alors, voici l'énoncé :
Un réfractomètre de Pulfrich sert à mesurer l'indice de réfraction d'un liquide afin de contrôler sa pureté ou sa composition chimique. Le principe est le suivant : sur un bloc de verre de section rectangulaire, d'indice N connu, on dépose une goutte de liquide dont on veut déterminer l'indice n.
Un faisceau lumineux monochromatique jaune pénètre dans le bloc de verre sur la face AB avec un angle d'incidence i1 : il se réfracte, puis se propage dans le verre et rencontre la surface de séparation entre le verre et le liquide. Ce faisceau peut alors se réfracter dans la goutte de liquide.
Lors d'une mesure on fait varier i1 jusqu'à avoir i4 = 90,00° ; on peut ainsi déterminer l'indice n en mesurant i1 avec une grande précision.
L'indice de réfraction de l'air est pris égal à 1,000.
1. Ecrire les relations qui existent entre les angles :
a. i1 et i2 ;
b. i2 et i3 ;
c. i3 et i4
2. On a déposé une goutte de glycérine sur le bloc de verre d'indice N = 1,652. On mesure i1 = 48,06°.
Calculer l'indice de réfraction de la glycérine pour la radiation jaune utilisée.
pour le schéma: 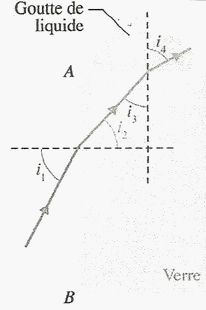
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
Bonjour,
L'image est vraiment de très mauvaise qualité.
Que proposes-tu ?
. Entre i1 et i2 : relation de Snell-Descartes
. Entre i2 et i3 : le bloc de verre a une section rectangulaire, donc...
. Entre i3 et i4 : relation de Snell-Descartes
À toi d'écrire ces relations.

Bonjour, j'avais pensé:
1.n1 sin i1= N sin i2
I1= sin -1(N sin i2/n1)
A peu près la même démarche pour le trois.
Et pour le 2 j'ai démontré que les des normales faisaient un angle droit et que donc:
I2= 180-(90+i3)
I3= 180-(90+i2)
Merci pour votre aide
j'espère ne pas m'être trompé.
C'est cela.
Dans un triangle rectangle la somme des deux angles aigus vaut 90°
_____________
Je t'en prie et à une prochaine fois !

n1.sin(i1) = N.sin(i2)
i3 = 90° - i2
N.sin(i3) = n.sin(i4)
---
N.sin(i3) = n.sin(i4)
N.sin(90°-i2) = n.sin(i4)
N.cos(i2) = n.sin(i4)
et comme i2 est aigu :
N.V(1-sin²(i2)) = n.sin(i4) (avec V pour racine carrée)
N.V(1- n1²sin²(i1)/N²) = n.sin(i4)
n = [N.V(1- n1²sin²(i1)/N²)]/sin(i4)
n = [V(N²- n1²sin²(i1))]/sin(i4)
On ajuste i1 pour avoir i4 = 90° (et donc sin(i4) = 1) -->
n = V(1,652² - sin²(48,06°))
n = 1,475
L'indice de réfraction de la glycérine est 1,475
-----
Sauf distraction. 


