Inscription / Connexion Nouveau Sujet
Principe d'inertie
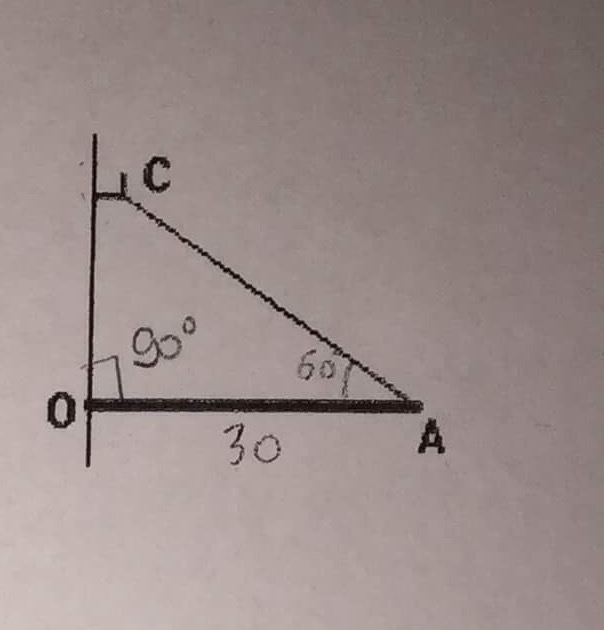
Une étagere est constituée par une planche homogene de masse m=2 kg, de longueur OA=f=30 cm. Elle est fixée au mur vertical par une articulation d'axe A horizontal. La planche est retenue par un cable AC. On donne OAC=60° et g=9,8 N/kg. Déterminer l'équilibre, la tension du fil AC et la réaction du mur en o.
Je pense que R+T=P donc R+T+P=0 mais je n'ai aucune valeur et J'ai fait plusieurs schéma avec différentes échelles (par exemple 1cm=5Newton) mais je ne comprends pas comment je peux trouver deux inconnues (j'ai essayé d'utilisé l'angle mais ma professeure nous as de ne pas utiliser la trigonométrie)
** image supprimée => un énoncé est à recopier (seul le schéma peut être inséré) et 1 topic = 1 exercice **
Bonjour.
En effet selon le principe d'inertie (attention c'est vectoriel).
Ensuite il faudrait projeter tes vecteurs suivant deux axes d'un repère centré sur O. Avec l'axe y orienté vers le haut et l'axe x vers la droite.
Tu auras donc un Px+Tx+Rx = 0 et Py+Ty+Ry = 0. Cependant Px = 0 et Ry = 0. Donc ça se simplifie et il faudra projeter T suivant x et y et sans utiliser l'angle de 60° je ne vois pas comment ça serait possible.
Vois-tu ?
Merci beaucoup, j'ai compris pour le répère mais comment pourrais-je exprimer exprimer mon résultat en Newton ? Et je ne comprend pas non plus comment je pourrais trouver T
.
N'en déplaise à ta prof si on projette dans le repère la trigo va pointer le bout de son nez.
As-tu essayé de le projeter sur l'axe x et sur l'axe y ? Qu'obtiens-tu ?
Une fois que c'est fait c'est quasiment terminé.
Oui... Et Rx = R et Py = -P car ils sont intégralement orientés suivant les deux axes distinctifs (P étant dans le sens opposé à y). C'est ok ?
La question reste la même T n'est pas orienté suivant un des deux axes, il faut le projeter.
Donc selon toi que vaut Tx et Ty ? Ils seront exprimés en fonction de T c'est comme ça que tu vas le trouver.
Je pense que Tx=T et que Ty=-T ?
Est ce que je pourrais créer un autre repère en prenant O pour origine, le vecteur OC pour l'axe des x et le vecteur OI pour l'axe des y (I serait le milieu de [OA] Et serait dans la même orientation que le vecteur T)?
Est ce que je pourrais créer un autre repère en prenant O pour origine, le vecteur OC pour l'axe des x et le vecteur OI pour l'axe des y (I serait le milieu de [OA] Et serait dans la même orientation que le vecteur T)?
Surement pas, quand on fixe un repère c'est pour la vie
. Si tu changes ton repère les autres forces exprimées dans le précédent repère ne seront plus correctes (sauf certains cas mais il y aura certainement des problèmes et c'est pas ce qu'on veut).
Tu dis que Tx = T . Bien sur que non car ça voudrait dire que T est intégralement orienté suivant l'axe x or ta force
Alors il faut revoir les relations qui découlent du cercle trigonométrique. Je te conseille de revoir une fiche de cours à ce sujet et de comparer avec ton exercice afin de bien comprendre comment se réalise une projection dans un repère orthonormé suivant l'axe x et l'axe y. Quoi qu'il en soit si on se place dans un triangle et là c'est le cas, on a :
cos() = côté adjacent à l'angle
/ hypoténuse et sin(
) = côté opposé à l'angle
/ hypoténuse.
Je connais déjà ces règles de trigonométrie mais l'exercice n'est pas faisable sans celles-ci ? Ma professeure ne nous as pas donné de cours sur le principe d'inertie et nous ad demandé de faire l'exercice sans trigonométrie.
J'ai eu l'idée de faire l'exercice avec une échelle et donc un schéma proportionnel cm/Newton mais je ne pense pas que ce soit une bonne idée.
Honnêtement je ne vois pas comment on pourrait faire sans passer par la trigo.
Ou bien mais il faudrait trouver une deuxième équation indépendante.
Tu n'as rien oublié dans l'énoncé ?
Bonsoir,
Je me pose des questions sur cet exercice.
L'énoncé indique que la l'étagère est fixée au mur vertical en A, mais sur la figure le seul point de contact entre l'étagère et le mur est en C.
Autre chose : Pour qu'un corps soit en équilibre sous l'action de trois forces il faut non seulement que la somme vectorielle de ces trois forces soit nulle, mais il faut aussi que la somme des moments de ces forces soit également nulle, ce qui en pratique implique que les directions de ces forces soient concourantes.
Dans ces conditions la composante Ry de ne peut pas être nulle.
D'ailleurs l'énoncé n'évoque pas l'absence de frottements au niveau du mur.
La force n'est probablement pas horizontale.
En France l'étude des moments n'est pas au programme de seconde , mais peut être que lina 6 est dans un autre système scolaire ...
mais sur la figure le seul point de contact entre l'étagère et le mur est en C.
Zut !
J'ai voulu dire :
mais sur la figure le seul point de contact entre l'étagère et le mur est en O.
Bien vu, ça expliquerai pourquoi il y a une longueur donnée .
Dans ce cas en effet le torseur dynamique est nul est on a bien deux équations indépendante.
Tu es scolarisée en France en seconde ?
Alors on a oublié une propriété métrique dans les triangles rectangles. 
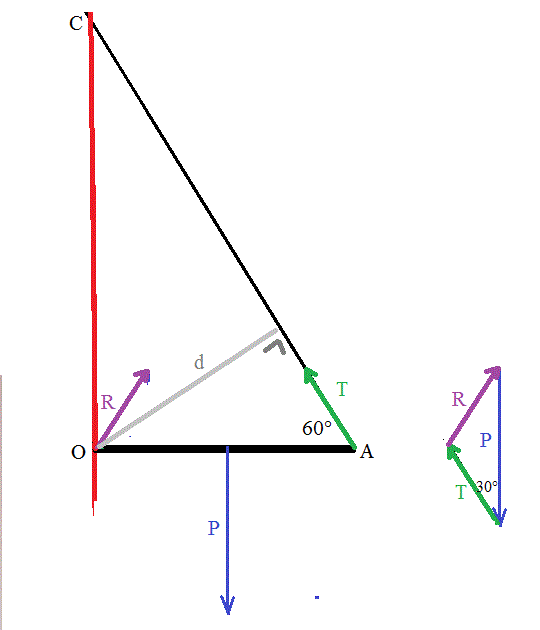
La planche ne tourne pas autour de 0 --> la somme des moments des forces sur la planche par rapport à O est nulle.
P * L/2 - T * d = 0
P.L/2 - T * L.sin(60°) = 0
m.g.L/2 = T * L * sin(60°)
m.g/(2.sin(60°)) = T
T = 2 * 9,8/(2 * (V3)/2)= 2 * 9,8/V3 = 11,3 N
P = 2 * 9,8 = 19,6 N
R² = P² + T² - 2.P*T.cos(30°)
R² = ...
R = 11,3 N
-----
Sauf distraction.
Sauf distraction.
Bien que souvent distrait, j'étais arrivé au même résultat.
Remarque : La donnée OA = 30 cm est redondante.
@lyna6 : Je serais curieux de savoir comment ton professeur va corriger cet exercice sans utiliser de trigonométrie.
Ry n'a aucune raison d'être nulle.
En effet !
Je serais curieux de savoir comment ton professeur va corriger cet exercice sans utiliser de trigonométrie.
Moi aussi !
Sans trigono est un peu forcé, néanmoins on peut se limiter aux triangles rectangles... qui est au programme de 3ème (me semble-t-il)
La composante horizontale de T ne peut être compensée que par la composante horizontale de R.
--> Rx = T.cos(60°)
Ry = P - T.sin(60°) (Projection des forces sur un axe vertical)
Et comme la planche ne pivote pas autour de O --> P*L/2 = T*L*d
P/2 = T*sin(60°)
On a donc un système de 3 équations à 3 inconnues (Rx, Ry et T) :
Rx = T.cos(60°)
Ry = P - T.sin(60°)
P/2 = T.sin(60°)
Ry = P - P/2 = P/2
T = P/(2.sin(60°))
Rx = P/(2.sin(60°))*cos(60°) = (1/2).P/tan(60°)
R = P/2 * RCarrée(1 + 1/tan²(60°)) = P/(2.sin(60°))
Sauf distraction.
J-PJ-P
La planche ne tourne pas autour de 0 --> la somme des moments des forces sur la planche par rapport à O est nulle.
P * L/2 - T * d = 0
P.L/2 - T * L.sin(60°) = 0
m.g.L/2 = T * L * sin(60°)
m.g/(2.sin(60°)) = T
T = 2 * 9,8/(2 * (V3)/2)= 2 * 9,8/V3 = 11,3 N
P = 2 * 9,8 = 19,6 N
R² = P² + T² - 2.P*T.cos(30°)
R² = ...
R = 11,3 N
-----
Sauf distraction.
Je ne comprends pas ce que le "L" dans "P*L" représente ?
Merci beaucoup pour votre aide mais j'ai juste une dernière question. Pourrais-je trouver les valeurs des forces exercées graphiquement ?
Une alternative économisant la trigonométrie :
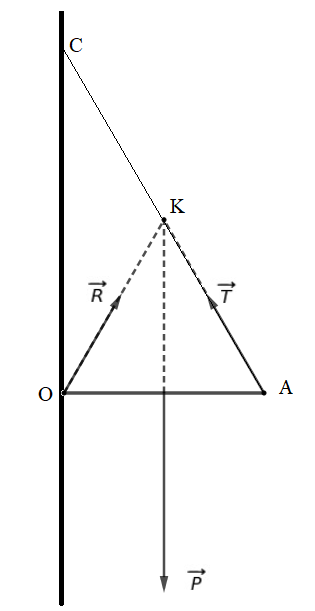
Je détermine le point de concours K des directions de et
Les trois forces étant concourantes je construis la direction de selon la droite OK
On a alors : Rx = Tx
La symétrie de la figure obtenue montre que Ry = Ty
donc 2Ry = m*g
Ry = m*g/2
R*sin(60°) = 2 * 9,8 / 2 = 9,8
R = 9,8 / sin(60) = 11,3N
J'ai donc contourné la condition d'équilibre de rotation du système par une condition équivalente : les trois forces ont des directions concourantes
Pour trouver la tension du fil, on a :
P= 19,6 N
R=11,3 N
Donc P+R+T=0
19,6+11,3+T=0
30,9+T=0
T=-30,9
Une force peut-elle être négative ?
Non
Tx = Rx
Ty = Ry
Les forces et
ont les mêmes composantes.
Elles ont aussi le même module :
T = R = 11,3N
Annuler
connectez vous