Le livre est immobile donc les forces se compensent --> principe d'inertie. Inventaires des forces: son poids et R le frottement qui compense ce poids.

Oups pardon je n'avais pas vu que c'était à partir de la 3) et 4) que tu n'y arrivais pas

rebonjour,quelle relation peut on mettre en évidence ici??

pas sur (je viens à peine de commencer la lecon sur les forces :S

bonjour
comme a dit infophile, le livre est immobile donc la somme des forces est nulle.
pour le dessin, la direction du poids est connue alors tu peut déduire celle du frottement puisqu'elles se compensent....

Bonsoir rémi,
tu as vu le principe d'inertie n'est-ce pas?
Comme le livre ne bouge pas on a
F(extérieures)=0 (vecteur nul)
Donc P+R+F=0

Voilà pour la 3, je te conseille de faire le schéma (au brouillon vite fait en premier) il aide bien, en sachant que le poids est dirigé vers le bas et la réaction du support est vers le haut et perpendiculaire à celui-ci.
Grâce à la constuction tu devrais pouvoir avancer déjà, tiens nous au courant si la 4 est encore problématique.
Bonne chance, a+. h

et désolé je ne maitrise pas le latex donc mes vecteurs sont immondes!

Bonjour!

Comme le livre ne glisse pas, tu sais que la force qui correspond au poids du livre compense la force de glissement.

Tu as donc: P= -R (avec des vecteurs sur P et R)
      c-à-d: mg= -R (avec des vecteurs sur g et R)

Si tu défais les vecteurs, tu as en projection sur les axes:
P cos =0 (sur l'axe Ox)
-P sin+R=0 (sur l'axe Oy)

Pour la représentation, tu as: (ATTENTION! Elle n'est pas à l'échelle...)

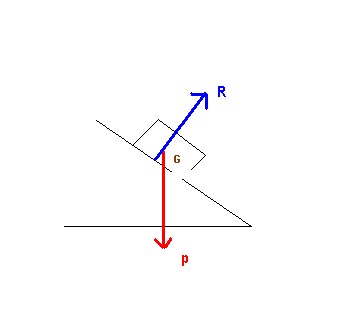
Bonsoir rémi,

Les trois forces s'exerçant sur le livre son le poids, la réaction du support et les forces de frottement comme déssiné ci-dessous.

Comme le livre est en équilibre on a alors :



pour dessiner les forces à l'échelle j'ai bien peur qu'il manque des données dans l'énoncé en effet on peut représenter le poids sans problème mais pour les autres cela me paraît difficile avec les seules données que tu nous énonces.

Salut

Cette fois lolo grillée (je plaisante ta démonstration est bien plus complète ).

Pour azarel, en Latex les vecteurs se traduisent par: \vec{le nom de ton vecteur} sans oublier les balises ce qui donne:

@peluche tout le monde

Merci bcp de m'avoir expliqué!

Ou là là....

J'ai oublié de préciser que le vecteur R sur mon schéma n'est pas (contrairement aux apparences...) perpendiculaire au plan.

J'ai déssiné R total= R (perpendiculeire) + F

oui, infophile, grillé pour cette fois 1 partout :P