Inscription / Connexion Nouveau Sujet
Optique - calcul de la valeur max de î pour une reflexion totale
Bonjour,
J'ai un problème d'optique à résoudre que nous n'avons pas résolu en classe.
Pouvez-vous vérifier si ma méthode de raisonnement est correct ainsi que mon résultat.Dans ma méthode de raisonnement, j'essaie de généraliser la méthode de résolution pour ce type d'exercice.
Enoncé
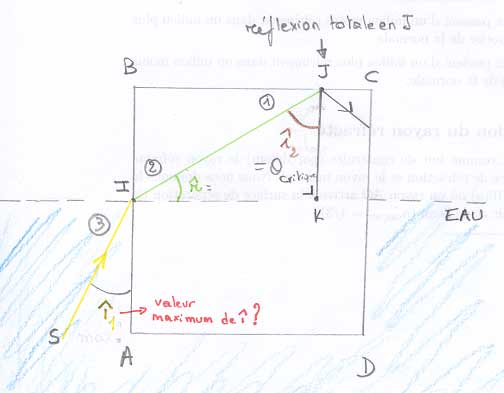
Un cube de verre est immerge dans l'eau; un rayon SI situé dans le plan perpendiculaire aux arêtes ABCD, aborde la face AB sous une incidence î.
Quelle doit être au maximum la valeur de î pour que le rayon subisse la réflexion totale en J ?
Schématisation du problème
Raisonnement Méthode : .
1) Il y a réflexion totale sur la face si l'angle d'incidence est supérieur à l'angle critique. On détermine la valeur de θcritique à partir de la loi de Descartes en posant θincident = θcritique et θa (de l'autre milieu)= 90° qui est déterminée par l'équation
ni sin θincident= na
2) A partir de cette équation, il est facile de déduire l'angle critique
Lorsque l'on a l'angle critique θ, on peut facilement déduire l'angle = 90 - θ
3) En appliquant la loi de Snell-Descartes pour la face AB, on peut déduire l'angle i
Données
N verre = 1,5 = 3/2
N eau = 1,33 = 4/3
Résolution
1) En J : sin θ = n1/n2 sin 90° => θ = 62,73°
2) = 90° - θ => 90° - 62,73° = 27,27°
3) n eau * sin î = n verre sin => sin î = 1,5/1.33 sin 27,27° => î = 31,12°
Une question : dans différents exercices, je vois qu'on utilise parfois sin θ = n1/n2 et parfois sin θ = n2/n1. Je n'arrive pas à savoir pourquoi on utilise l'une ou l'autre. Si vous pouvez m'éclairer sur ce point, n'hésitez pas.
Merci pour votre aide
Hop ! un petit saut dans le forum
je vais y réfléchir...ca fait lontemps que j'ai fait ce chapitre je ne m'en souviens plus très bien .;s'est le moment de m'y remettre!!
bjr kiki02 je voudrais savoir ce que signifie le symbôle que tu as mis ....l'éspéce de 0 aec une barre....
Bonjour à tous les deux 
tokiohotel59 >> Il s'agit d'une lettre grecque, qui sert ici à nommer l'angle.
Estelle 
Une question : dans différents exercices, je vois qu'on utilise parfois sin θ = n1/n2 et parfois sin θ = n2/n1. Je n'arrive pas à savoir pourquoi on utilise l'une ou l'autre. Si vous pouvez m'éclairer sur ce point, n'hésitez pas.
je pense que cela dépend du sens dans lequel du prend ta formule... Mais je comprend pas très bien ce que tu veux dire... Cela dépend aussi de ce qu'on te demande de chercher...
d'accors .mais offéte qu'est ce qu'il entend par angle critique???le dioptre??
En effet, moi aussi je pense que c'est juste mais si Coll passe par là.....
j'aimerai avoir sa confirmation...
Et ma question (je vois qu'on utilise parfois sin θ = n1/n2 et parfois sin θ = n2/n1) reste toujours en suspens. Je voudrai savoir si c'est une erreur dans mes notes ou si cela dépend du milieu dans lequel passe la lumière (+ ou - réfringent)....
Je sais pas trop, faudrait que Coll confirme... Moi je pense que ça dépend de la situation dans laquelle tu te trouves...
Bonjour,
Une petite info pour ta question:on utilise parfois sin θ = n1/n2 et parfois sin θ = n2/n1
La seule relation que l'on a est en fait n1. sin i1 = n2. sin i2
avec le rayon qui se déplace du milieu 1 vers le milieu 2.
Lorsque tu cherches l'angle d'incidence i1 qui correspond au plus grand angle de réfraction possible, tu as i2=90° et donc sin i2 = 1 d'où i1= n2/n1
Lorsque tu cherches le rayon réfracté pour i1 = 90° alors sini1 = 1 et donc i2 = n1/n2
Je pense que ta confusion vient du fait que dans les deux cas l'angle 
ne represente pas la même chose. Tantôt c'est un angle incident , tantôt c'est le réfracté.
Bonjour sariette,
Ok pour ton explication est claire et en effet, ma confision vient de là.
Je prépare un examen de passage en septembre et l'optique n'est pas mon fort.
Est-ce que tu penses que l'exercice ci-dessus est correct ?
Merci de ta réponse.
Bonjour,
Une petite info pour ta question
n utilise parfois sin θ = n1/n2 et parfois sin θ = n2/n1
La seule relation que l'on a est en fait n1. sin i1 = n2. sin i2
avec le rayon qui se déplace du milieu 1 vers le milieu 2.
Lorsque tu cherches l'angle d'incidence i1 qui correspond au plus grand angle de réfraction possible, tu as i2=90° et donc sin i2 = 1 d'où i1= n2/n1
Lorsque tu cherches le rayon réfracté pour i1 = 90° alors sini1 = 1 et donc i2 = n1/n2
Je pense que ta confusion vient du fait que dans les deux cas l'angle ne represente pas la même chose. Tantôt c'est un angle incident , tantôt c'est le réfracté.
Je pense que c'est ce qu'on essayait d'expliquer avec tokiohotel59...sans succès...
Message pour J-P correcteur
Bonjour J-P correcteur,
Comme je vois que tu es en ligne peux-tu me dire si mon exercice est correct ?
Merci de ton aide
Il ne peut pas savoir que tu as besoin d'aide à part s'il regarde ce topic...
Mais ne t'en fais pas, je lui ai demandé de venir...
J'espère qu'il jettera un oeil à ton exo
bonsoir kiki02,
désolée de répondre si tard , l'alerte message vient à peine de tomber...
Ton raisonnement est juste . Cependant tout à la fin l'angle i de la formule est défini par rapport à la normale . Ce n'est donc pas celui que tu as dessiné, mais son complément à 90.
merci à J-P de vouloir bien confirmer.
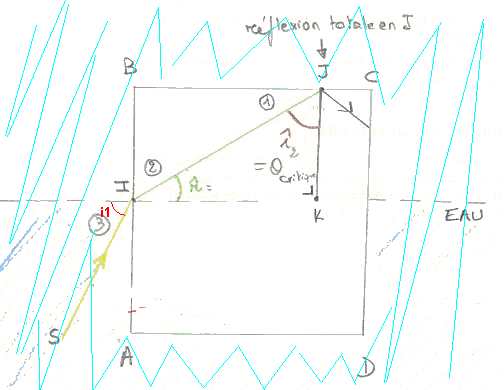
Attention, au passage eau-air (en I), l'angle d'incidence n'est pas où tu l'as indiqué.
L'angle est mesuré entre la rayon et la normale à la surface au point d'incidence.
En J:
n2.sin(i2) = n1.sin(r2)
sin(r2) = (n2/n1).sin(i2)
on a réflexion totale si (n2/n1).sin(i2) >= 1
((3/2)/(4/3)).sin(i2) >= 1
(9/8).sin(i2) >= 1
sin(i2) >= 8/9
i2 >= 62,73°
soit r <= 90-62,73
r <= 27,27°
En I:
n1.sin(i1) = n2.sin(r)
(4/3).sin(i1) <= (3/2).sin(27,27°)
sin(i1) <= ((3/2)/(4/3)).sin(27,27°)
sin(i1) <= (9/8).sin(27,27°)
sin(i1) <= 0,515
Si i1 <= 31°, , il y a réflexion totale.
Donc la valeur max de i1 pour qu'il y ait réflexion totale sur la face BC est 31°
-----
Sauf distraction.
Merci sarriette et Jp-correcteur pour vos explications et vos corrections,
je peux donc mettre mon exercice dans mes fiches de révisions pour mon examen de passage de septembre ....
Encore merci
Complément à ma réponse.
Si i1 devient trop petit, le rayon réfracté dans le verre (en vert sur le dessin) n'arrivera plus sur la face BC du verre et alors plus question non plus de réflexion totale sur la face BC.
Donc la valeur max de i1 pour qu'il y ait réflexion totale sur la face BC est bien de 31°, mais si i1 devient trop petit il n'y a plus réflexion totale et donc on ne peut pas écrire comme je l'ai fait: "Si i1 <= 31°, il y a réflexion totale".
Ok J-P correcteur, je te remercie encore 1000 fois
La réponse 31° etait elle juste svp, car j'ai le meme exercice en DM et je n'ais pas trouvé pareil, merci de votre reponse
Annuler
connectez vous