Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie

1 2 3 +

Niveau licence
Partager :

mouvement dans un trajet circulaire avec frottement

Posté par
praf 14-11-20 à 11:47

salut
une particule de masse m de vitesse initial V0 parcours un trajet circulaire avec frottement constante f
quel est l'angle maximale atteint par le particule?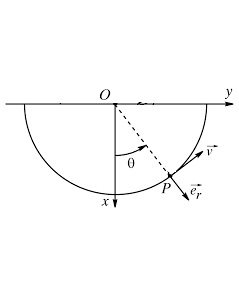

mouvement dans un trajet circulaire avec frottement

**modération > forum mis en adéquation avec le profil renseigné**

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 14-11-20 à 11:52

Bonjour
Le théorème de l'énergie cinétique , tu connais ? Je te laisse faire une proposition de solution.

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 14-11-20 à 11:56

Remarque complémentaire : pour t'aider vraiment, il faudrait un énoncé complet de l'exercice...

***Edit gbm => praf : lire attentivement ceci [***A LIRE AVANT D'AGIR***] Règles du forum***

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 16-11-20 à 17:48

merci pour ton réponse
l'énoncé de l'exercice est complète
pour lethéorème de  l'énergie cinétique
1/2mVθ=max2-1/2mV02=w(p)+w(R)+w(f) =-mgr(1-cosθ)-frθ
car à l'angle maximale la vitesse s'annule a θmax et w(R)=0
donc 1/2mv0=mgr(1-cosθ)+frθ
j'obtient une équation en cosθ et θ et je me bloc
merci

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 16-11-20 à 18:29

Si je comprends bien il faut imaginer une petite perle enfilée sur un cerceau de rayon r, placé dans le champ de pesanteur uniforme, le plan du cerceau étant vertical, la perle de masse m, passant en =0 avec une vitesse Vo. Cela fait beaucoup d'hypothèses à faire. Il n'existe pas de solution mathématique simple à l'équation obtenue. Il faut faire une résolution graphique ou une résolution numérique avec une calculatrice scientifique ou un ordinateur.
Encore une fois : difficile de t'aider efficacement car l'énoncé est très incomplet.
PS : étourderie sans doute : tu as oublié le "carré" de Vo dans ta dernière formule.

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 17-11-20 à 16:17

merci beaucoup
l'exercice c'est comme tu as énoncer et on a le cerceau exerce une force de frottement constante f sur le point matériel
oui exactement j'ai oublié de mettre v0 au carré

donc l'équation obtenu pas de solution  
merci

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 17-11-20 à 17:22

Pas de solution littérale ; solution numérique possible.

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 19-11-20 à 15:15

merci pour votre réponse
est ce qu'on peut obtenir l'équation de mouvement
c-à-d θ(t) en fonction de θ on considérer θ0 assez grand
c-à-d on ne peut pas faire sinθ=θ
merci

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 19-11-20 à 17:38

Tu peux obtenir une réponse concernant la valeur maximale de atteinte, en supposant la vitesse initiale pas trop élevée pour que cet angle reste petit. Tu peux alors effectuer un développement du cosinus limité à l'ordre 3 qui conduit à :

1-\cos\left(\theta\right)\approx\dfrac{\theta^{2}}{2}

Tu obtiens alors une équation du second degré en que tu peux résoudre.
Tant que ne dépasse pas 20°, l'erreur relative commise reste inférieure à 1% ; tant que ne dépasse pas 44°, l'erreur relative commise reste inférieure à 5°.
Ecrire le théorème de l'énergie cinétique pour une position d'angle quelconque puis  dériver par rapport au temps cette expression conduit à une équation différentielle vérifiée par =f(t) que tu peux résoudre dans le cadre de l'approximation précédente.

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 21-11-20 à 09:19

merci beaucoup

Posté par
Chimivalre : mouvement dans un trajet circulaire avec frottement 22-11-20 à 15:00

Bonjour,

Ma question s'adresse plutôt à Vanoise : dans cet exercice, on a considéré que la force tangentielle  de frottement était -fT où T est le vecteur tangent  et f = constante ;
- Question : Si f n'avait été que le coefficient de frottement, alors la force de frottement F   aurait  été F = -f*m*g*cos(téta)*T,   non ?

  Cordialement

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 22-11-20 à 15:06

Bonjour Chimival
Tu as raison et le problème aurait encore été un peu plus compliqué...

Posté par
Chimivalre : mouvement dans un trajet circulaire avec frottement 22-11-20 à 16:20

Bien reçu,

     Merci Vanoise,

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 26-11-20 à 16:22

pour chimival et vanoise
soit µ le coefficient de frottement
on a f=µ*RN
on doit déterminer RN
R.F.D projécter a la composante normale de repère de Frenet donne
RN-mgcos(θ)=mv2/2
pour déterminer v
on utlise le théoreme de l'energie cinétique. on obtient :
1/2mv2-1/2mv02=-mgr(1-cos(θ))-f.R.θ
c-à-d:
1/2mv2-1/2mv02=-mgr(1-cos(θ))-.R.θ.µ.RN
je trouve deux inconnu RN et v
ou je trompe?

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 26-11-20 à 18:00

La situation est un peu plus compliquée que cela : comme je vais le montrer plus bas, la force de frottement tangentielle ne garde pas une intensité fixe au cours du mouvement : l'expression de son travail n'est donc pas égale au produit de l'intensité de la force par la distance parcourue. Il me semble préférable de passer par la relation fondamentale de la dynamique :

m.\overrightarrow{a}=\overrightarrow{P}+\overrightarrow{R_{T}}+\overrightarrow{R_{N}}

On projette sur un axe normal centrifuge :

-m.a_{N}=m.g.\cos\left(\theta\right)-R_{N}

avec l'accélération normale : a_{N}=r.\dot{\theta}^{2} ( \dot{\theta}=\frac{d\theta}{dt}  :  vitesse angulaire)

R_{N}=m.g.\cos\left(\theta\right)+m.r.\dot{\theta}^{2}

Loi de Coulomb sur le frottement solide :

R_{T}=\mu.R_{N}=\mu.\left[m.g.\cos\left(\theta\right)+m.r.\dot{\theta}^{2}\right]

On projette maintenant sur un axe tangent à la trajectoire orienté dans le sens positif :

m.a_{T}=-m.g.\sin\left(\theta\right)-R_{T}

avec l'accélération tangentielle : a_{T}=r.\ddot{\theta}   (\ddot{\theta}   :   accélération angulaire, dérivée par rapport au temps de la vitesse angulaire). Au final, l'équation différentielle vérifiée par l'abscisse angulaire s'écrit :

m.r.\ddot{\theta}=-m.g.\sin\left(\theta\right)-\mu.\left[m.g.\cos\left(\theta\right)+m.r.\dot{\theta}^{2}\right] \\ \\ \ddot{\theta}+\mu.\dot{\theta}^{2}+\frac{g}{r}\cdot\left[\sin\left(\theta\right)+\mu.\cos\left(\theta\right)\right]=0

Rien de très simple, même dans le cas où l'angle reste faible.

Posté par
Chimivalre : mouvement dans un trajet circulaire avec frottement 26-11-20 à 19:59

Bonsoir Praf, Bonsoir Vanoise,


Merci pour vos réponses, je vais y réfléchir ;
-Pour Vanoise : y a t-il un moyen de convertir la réponse du Latex en écriture normale ?

  Cordialement,

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 26-11-20 à 21:20

Pas de chance  : le serveur latex du site est en panne ce soir.  Les choses devraient rentrer dans l'ordre demain. Sinon tu as toujours la ressource de copier-coller ma réponse dans un traitement de texte qui accepte le code  tex, Lyx par exemple.

***Editeur \LaTeX réparé le soir même ***

Posté par
Chimivalre : mouvement dans un trajet circulaire avec frottement 27-11-20 à 11:44

Bonjour Vanoise, bonjour praf,

Merci à Vanoise pour sa démo ;

Pour praf : le théorème de l'énergie cinétique entre téta 0 et téta c'est, à mon avis :
1/2mv2 - 1/2mv02 = - mgR[cos(téta 0) - cos(téta)] - Intégrale de [mu*Rn*R(dtéta)] entre téta 0 et téta ;
Et comme dit Vanoise c'est difficile à exploiter,
     Cordialement

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 28-11-20 à 09:26

merci mes amis
donc si on a seulement le coefficient de frottement, il est impossible de déterminer la vitesse à une position donné θ ni la réaction de la rail circulaire sur le point matériel RN,
n'est ce pas ?

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 28-11-20 à 09:35

Dans le cas le plus général, on peut résoudre l'équation différentielle par une méthode numérique à l'aide d'un ordinateur ou d'une calculatrice programmable : méthode d'Euler, méthode de Runge Kutta...

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 28-11-20 à 11:51

Bien comprendre,

     Merci Vanoise.

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 28-11-20 à 12:11

A titre d'illustration, voici la courbe =f(t) dans le cas particulier suivant :
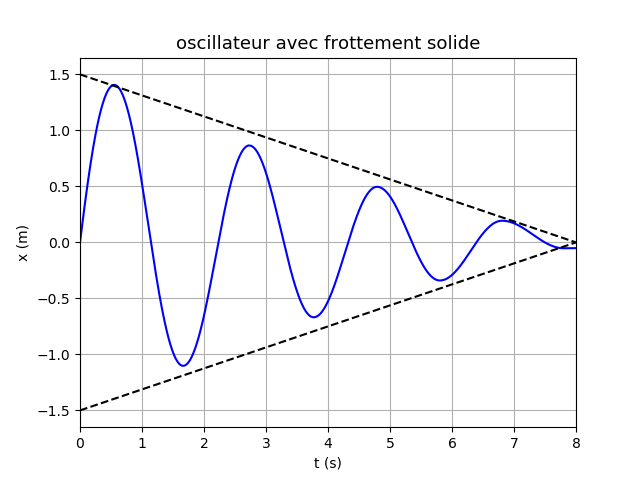
r=1m ; Vo=4.5m/s et µ=0,07. On peut remarquer que le premier arrêt s'obtient pour m1,4rad.
Le solide repart alors en sens inverse et on obtient des oscillations amorties. J'ai aussi représenté la courbe =f(t) que l'on obtiendrait en cas de frottement fluide : force de frottement proportionnelle à la vitesse.

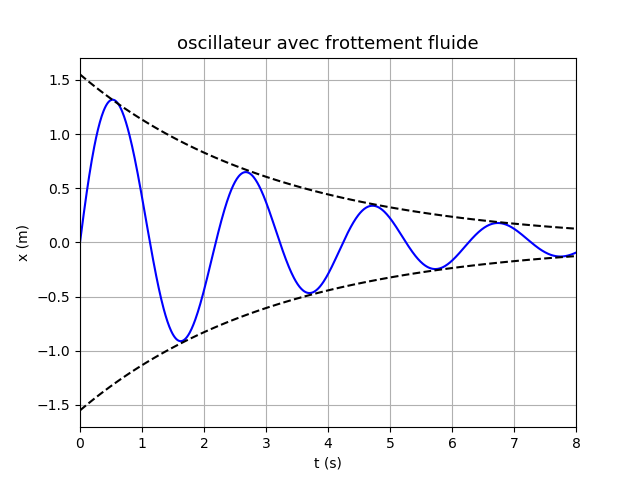
mouvement dans un trajet circulaire avec frottement

mouvement dans un trajet circulaire avec frottement

Posté par
Chimivalre : mouvement dans un trajet circulaire avec frottement 28-11-20 à 14:14

Bonjour Vanoise,

Merci

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 30-11-20 à 15:46

Bonjour Vanoise,
les graphes sont pour des  v0 qui laisse  θm faible
n'est ce pas?

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 30-11-20 à 17:00

Non : m=1,4rad80°
C'est bien pour cela qu'il s'agit d'une simulation numérique. Les courbes obtenues n'admettent pas d'équations littérales.

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 01-12-20 à 15:57

merci  Vanoise
et pour la période on peut le préciser d'une manière  littérale ou seulement numériquement ?

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 05-12-20 à 10:57

je trouve dans certain référence
pour le mouvement sans frottement
avec k(x) est le fonction elliptique de Jacobi

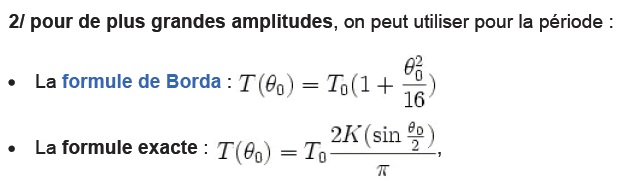
mouvement dans un trajet circulaire avec frottement

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 05-12-20 à 11:33

Bonjour
Tu vas trouver dans le document suivant la démonstration de l'expression exacte de la période et la démonstration de l'expression de Borda :

Voir partie III.3, essentiellement les paragraphes III.3.2 et III.3.3 ; le reste du document porte sur les balanciers de précision utilisés en horlogerie, donc hors sujet ici.
J'ai aussi eu l'occasion d'aider un étudiant sur ce sujet en poussant l'expression simplifiée de la période jusqu'à la puissance 4 de l'amplitude : voir mon message du 04-12-19 à 11:32 et le suivant ici :
pendule

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 05-12-20 à 12:03

merci beaucoup  Vanoise
pour un mouvement sans frottement c'est bien compris
pour le mouvement avec frottement qu'il y a les difficulté
j'ai cette exercice

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 05-12-20 à 12:10

De quel type de frottement s'agit-il ? Peux-tu poster l'énoncé intégral de l'exercice qui te pose problème ?

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 05-12-20 à 12:12

voila l'exercice

** image supprimée **

Posté par
gbm Webmasterre : mouvement dans un trajet circulaire avec frottement 05-12-20 à 12:39

Bonjour,

@ praf : je t'ai rappelé les règles :

attentionextrait de c_faq la FAQ du forum :

Q05 - Puis-je insérer une image dans mon message ? Comment faire ? Quelle image est autorisée ?



attentionextrait de c_faq la FAQ du forum :

Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?



Et 1 sujet créé = 1 exercice

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 05-12-20 à 12:46

Si l'exercice est en rapport avec les messages précédents, ma réponse du  26-11-20 à 18:00 devrait t'aider. Pour plus de précision, recopie les questions qui te pose problème comme demandé par le règlement du forum.

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 05-12-20 à 20:22

merci gbm pour votre rappel
je suis nouveau dans le forum et je prend les règle goutte a goutte

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 05-12-20 à 21:00

Bonsoir gbm
Pour avoir vaguement lu l'énoncé scanné (sans y avoir apporté d'aide ) je peux confirmer  : il s'agit bien de la suite logique  de l'étude commencée sur le pendule avec frottement solide.

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 05-12-20 à 21:28

merci   Vanoise
votre réponse du  26-11-20 à 18:00 a beaucoup résoudre le problème il reste seulement deux question
je vais présenter la totalité des question

La particule glisse maintenant avec frottement à l'intérieur du cercle, avec un coefficient de  frottement µ= T/N où T et N sont les valeurs des composantes tangentielle et normale de la réaction du cylindre sur M
1-Établir l'équation différentielle non linéaire du second ordre du mouvement
2- Mettre l'équation différentielle précédente sous la forme





Déterminer les coefficients numériques a, b et c.
3. la solution de l'équation différentielle est de la forme








reportant cette solution dans l'équation différentielle en x, et en procédant par identification, déterminer les coefficients A et B.En considérant l'état initial déterminer l'expression de K.

Exprimer θ.2(la vitesse angulaire θ point au carré) en fonction de θ, g et R.

3.En déduire la loi N(θ)
4.Calculer la valeur maximale θMde l'élongation.
5.calculer la durée t pour atteindre θM

** image supprimée **

** image supprimée **

** image supprimée **

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 05-12-20 à 21:35

pardon il y a un désordre entre les images et les question
je ne suis pas professionnel dans l'édition des message avec des image et j'ignore comment taper des caractère spéciaux comme θ point; racine carré....
l'image 1 et 2 concerne la question 2
l'image 3 concerne la question 3

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 05-12-20 à 21:39

bonsoir  Vanoise
pour les question 1 2 et 3
votre réponse du  26-11-20 à 18:00 et suffisant
les question 4 et 5 sont vague pour moi

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 05-12-20 à 22:41

La particule glisse maintenant avec frottement à l'intérieur du cercle, avec un coefficient de  frottement µ= T/N où T et N sont les valeurs des composantes tangentielle et normale de la réaction du cylindre sur M
1-Établir l'équation différentielle non linéaire du second ordre du mouvement

on mettre µ=1/4; V0=\sqrt{\frac{7}{5}gR}
et on pose x=(\overset{.}{\theta})^2
2- Mettre l'équation différentielle précédente sous la forme

\frac{dx}{dt} \ +ax=- \frac{g}{R}(b.cos\theta+c.sin\theta) \

Déterminer les coefficients numériques a, b et c.
3- a . la solution de l'équation différentielle est de la forme
x=k e-aθ - \frac{g}{R}(A.cos\theta+B.sin\theta) \
reportant cette solution dans l'équation différentielle en x, et en procédant par identification, déterminer les coefficients A et B.En considérant l'état initial déterminer l'expression de K.
Exprimer(\overset{.}{\theta})^2   en fonction de θ, g et R.
3-b.En déduire la loi N(θ)
4.Calculer la valeur maximale θMde l'élongation.
5.calculer la durée t pour atteindre θM

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 05-12-20 à 22:55

Si tu as réussi la question 3, il suffit d'écrire que =m lorsque le carré de la vitesse angulaire s'annule.

Posté par
gbm Webmasterre : mouvement dans un trajet circulaire avec frottement 06-12-20 à 12:46

vanoise @ 05-12-2020 à 21:00

Bonsoir gbm
Pour avoir vaguement lu l'énoncé scanné (sans y avoir apporté d'aide ) je peux confirmer : il s'agit bien de la suite logique de l'étude commencée sur le pendule avec frottement solide.

Bonjour vanoise, je viens de voir ton message. Oui, je suis peut-être allé trop vite sur le "1 sujet = 1 exercice" mais il est clair qu'il y avait une recopie de l'énoncé à faire (moins d'un A4).

Bon dimanche,

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 06-12-20 à 14:13

Concernant la copie de l'énoncé et l'équation différentielle : il ne s'agirait pas plutôt de \frac{dx}{d\theta} plutôt que de \frac{dx}{dt} ?

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 06-12-20 à 20:53

bonsoir
oui c'est un faute de tapage
l'équation différentielle est :
\frac{dx}{d\theta} \ +ax=- \frac{g}{R}(b.cos\theta+c.sin\theta) \
mon démonstration est comme celui ci :
l'équation de mouvement est :

\overset{..}{\theta} +µ\overset{.}{\theta}^2+\frac{g}{R}.(sin\theta+µcos\theta)=0        (1)
d'après votre démonstration dans votre  réponse du  26-11-20 à 18:00

\frac{1}{2} \frac{1}{dt}(\overset{.}{\theta})^2=\overset{.}{\theta}.\overset{..}{\theta}

et on a     \overset{.}{\theta}=\frac{d\theta}{dt}

donc \overset{..}{\theta}=\frac{1}{\overset{.}{\theta}}.\frac{1}{2}.\frac{d(\overset{.}{\theta})^2}{dt}

c-à-d:

\overset{..}{\theta}=\frac{dt}{d\theta}}.\frac{1}{2}.\frac{d(\overset{.}{\theta})^2}{dt}

Remplaçons dans (1) et on multipliant par 2 on trouve :

\frac{dx}{d\theta}} +2µx=-\frac{g}{R}.(2sin\theta+2µcos\theta)=0  

On trouve a=c=2µ ; b=2 ;

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 06-12-20 à 21:01

les autre calcul sont classique
on trouve
A=µ-1
et B=(1+µ)/2µ

et k=\frac{v_0^2}{R}+\frac{g}{R}.(µ-1)

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 06-12-20 à 21:07

pour déterminer \theta_M

on fait k e^{-a\theta} -  \frac{g}{R}(A.cos\theta+B.sin\theta) \ =0

une équation qui contient cos et sin et l'exponentiel

comment résoudre une tel équation ?

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 06-12-20 à 22:52

Je ne pense pas qu'il existe de solution explicite à cette équation. C'est aussi l'avis des mathématiciens qui ont répondu à des questions analogues sur divers forums de maths...
Reste donc une résolution numérique à l'aide d'une calculatrice scientifique ou d'un logiciel comme Matlab, Scilab, Maple...

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 07-12-20 à 12:34

J'ai répondu hier soir à ton message sur la résolution numérique sans avoir pris le temps de vérifier les résultats de ton message du  06-12-20 à 21:01.
Je suis d'accord avec tes valeurs de a, b et c mais pas avec tes valeurs de A, B et k. Peux-tu vérifier tes calculs ?

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 07-12-20 à 21:12

merci
je procede comme ça:

\frac{dx}{d\theta}} +2µx=-\frac{g}{R}.(2sin\theta+2µcos\theta)

x=k e^{-a\theta} -  \frac{g}{R}(A.cos\theta+B.sin\theta) \

\frac{dx}{d\theta}=-ak e^{-a\theta} -  \frac{g}{R}(-A.sin\theta+B.cos\theta) \

2µx=2µk e^{-a\theta} -  \frac{g}{R}(2µA.cos\theta+2µB.sin\theta) \

\frac{dx}{d\theta}+2µx=(2µ-a)k e^{-a\theta} -  \frac{g}{R}((2µ.A+B).cos\theta+(2µB-A).sin\theta) \
                                                                =-\frac{g}{R}.(2sin\theta+2µcos\theta)


donc (2µ-a)k =0 ce qui est évident car 2µ=a
et on a 2µ.A+B=2µ et 2µB-A=2

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 07-12-20 à 21:30

donc (2µ-a)k =0 ce qui est évident car 2µ=a
et on a  2µ.A+B=2µ et 2µB-A=2

2µ.(2µB-A=2) donc 4µ^2.B-2µA=4µ
(4µ^2+1)B=6µ
B=\frac{6µ}{4µ^2+1}

A=2µB-2=2µ.\frac{6µ}{4µ^2+1}-2=\frac{12µ^2}{4µ^2+1}-2=\frac{12µ^2-8µ^2-2}{4µ^2+1}-2=\frac{4µ^2-2}{4µ^2+1}

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 07-12-20 à 21:41

quand \theta=0   ; \overset{.}{\theta_0}=\frac{v_0}{R}


on a a x (\theta=0) =k- \frac{g}{R}.A

                                =\frac{v_0^2}{R^2}

k=\frac{v_0^2}{R^2}+ \frac{g}{R}.A

k=\frac{v_0^2}{R^2}+ \frac{g}{R}.\frac{4µ^2-2}{4µ^2+1}

1 2 3 +


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !