Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie

1 2 3 +

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 15-01-21 à 12:00

Tu oublies un terme dans ton équation différentielle :

\ddot{\theta} +\frac{k}{m}\dot{\theta}+\frac{g}{R}\cdot \sin(\theta)=0 \\
L'étude est très classique pour les faibles amplitudes. Tout se complique dès qu'il n'est plus possible de poser : \sin(\theta)\approx \theta ; Déjà en absence de frottement, l'équation différentielle n'admet pas de solution explicite ; donc avec frottement... Il faut se limiter à une simulation numérique. J'ai tout de même posé la question sur le forum de math, il y a sûrement des méthodes de résolution d'équations différentielles que j'ignore. Les réponses vont dans le même sens que la mienne. Voir ici :

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 17-01-21 à 20:15

Bonsoir vanoise,
merci pour votre réponse et pour vos efforts à m'aider,

je refaire les calculs plusieurs fois, j'arrive pas a détecter l'erreur et par suite le terme manquant dans mon équation différentielle.
merci.

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 17-01-21 à 21:12

Relis ton précédent message  : tu avais oublié le sinus.

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 17-01-21 à 21:26

c'est vrai, merci pour la correction
moi je vois votre équation dans l'île de math

\ddot{\theta}+2\lambda.\omega_{o}.\dot{\theta}+\omega_{o}^{2}.\sin\left(\theta\right)=0

il y a un  \omega_{o} dans le deuxième terme
d'ou vient-il?
( si on pose    \lambda=\frac{k}{2m})

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 17-01-21 à 21:51

Tel que j'utilise :
= 1/(2Q )  ; il s'agit ici d'un réel sans dimension physique.

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 17-01-21 à 22:13

ah bon, merci

donc il est difficile de traiter le cas ou la force de frottement   \overrightarrow{f}=-k\overrightarrow{v}

maintetnant si :

\\ \overrightarrow{f}=-k\overrightarrow{v}^2

l'équation obtenu est :


\\ \ddot{\theta} +\frac{k}{m}\dot{\theta}^2+\frac{g}{R}\cdot \sin(\theta)=0

il est semblable a l'équation de frottement solide que tu a démontrer précédent :\overset{..}{\theta} +µ\overset{.}{\theta}^2+\frac{g}{R}.(sin\theta+µcos\theta)=0      

donc ma question est ce qu'on peut suivre la même procédure pour trouver \dot\theta

c-à-d on pose x=\dot\theta^2

et Mettre l'équation différentielle précédente sous la forme

\frac{dx}{dt} \ +ax=- \frac{g}{R}(b.cos\theta+c.sin\theta) \

la solution de l'équation différentielle est de la forme
x=k e^{-a\theta} -  \frac{g}{R}(A.cos\theta+B.sin\theta) \

si cette idée est correcte je débauche les calcul pour déterminer les constante
si ce n'est pas le cas je cherche une autre méthode
merci d'avance



Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 18-01-21 à 11:26

La force de frottement est constamment de sens opposé au sens du vecteur vitesse et le carré d'un vecteur n'est pas un vecteur. Il faut donc écrire : \overrightarrow{f}=-k.\Vert\overrightarrow{v}\Vert.\overrightarrow{v}. L'équation différentielle que tu as écrite n'est valide que pour les vitesses angulaires positives. Pour une simulation informatique, on pourrait l'écrire sous la forme :

\ddot{\theta}+\frac{k}{m}\dot{\theta}.|\dot{\theta}|+\frac{g}{R}\cdot\sin(\theta)=0

Attention : cela avait été rectifié par chimival : on s'intéresse à la dérivée de x par rapport à l'angle, pas par rapport au temps :

\frac{dx}{d\theta}+ax=-\frac{g}{R}(b.\cos(\theta)+c.\sin(\theta))

Il est effectivement possible de trouver une solution de la forme :

x=ke^{-a\theta}-\frac{g}{R}(A.\cos(\theta)+B.\sin(\theta))

Cela sera valide tant que la vitesse angulaire restera positive ou nulle et on suppose qu'il s'agit d'un pendule rigide : le mouvement ne peut être que circulaire.

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 19-01-21 à 20:58

Bonsoir,
Bien reçu,
     Merci Vanoise,

je veux seulement corriger une faute dans mon message précédent
lorsque la force de frottement est  : \overrightarrow{f}=-k.\Vert\overrightarrow{v}\Vert.\overrightarrow{v}

l'équation différentielle sera (si je ne trompe pas):


\\ \ddot{\theta} +\frac{k.R}{m}\dot{\theta}^2+\frac{g}{R}\cdot \sin(\theta)=0

qui s'écrit sous la forme :


\frac{dx}{d\theta}+ax=-2.\frac{g}{R}(sin(\theta)) \\

avec     a=2.\frac{k.R}{m}

la solution de cette equation est : (avec   x=\dot\theta^2)

x=A e^{-a\theta} -  \frac{g}{R}(B.cos\theta+C.sin\theta) \

(je change les constantes puisque la force de frottement utilise k)
en remplace  j'obtient le systeme suivant:


\left\lbrace\begin{array}l C-aB=0 \\ aC-B=2 \end{array}

\left\lbrace\begin{array}l C=\frac{2a}{a^2-1} \\B=\frac{2}{a^2-1} \end{array}

les conditions initial: a t=0 :
on a v=v_0(ou \dot\theta_0=R.v_0)
après remplacement on trouve

A=\dot\theta_0^{2}+\frac{g}{R}.B

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 20-01-21 à 13:42

Je viens de reprendre tes calculs. Je peux me tromper bien sûr mais à mon avis :

\left\lbrace\begin{array}l C+a.B=0 \\ a.C-B=2 \end{array}
Étourderie dans les dernières lignes :

\dot\theta_o=\dfrac{v_o}{R}

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 20-01-21 à 20:53

Bonsoir Vanoise,
merci pour votre correction

oui c'est vrai  on trouve :


\left\lbrace\begin{array}l C+a.B=0 \\ a.C-B=2 \end{array}

je trouve :

B=\frac{-2}{1+a^2}    et   C=\frac{2a}{1+a^2}


pour A je refaire le calcul je trouve le même résultat :


A=\dot\theta_0^{2}+\frac{g}{R}.B

avec bien sur comme tu a mentionner :

\dot\theta_o=\dfrac{v_o}{R}

maintenant je voir comment calculer la vitesse initiale minimale pour que le pendule effectue un tour complet :

*on utilise l'expression de \dot\theta_2=A e^{-a\theta} -  \frac{g}{R}(B.cos\theta+C.sin\theta) \    ( on suppose que la tige est rigide et la réaction R_N ne s'annule pas)

*ou on passe nécessairement par le théorème de l'énergie cinétique

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 21-01-21 à 12:57

   D'accord maintenant avec tes calculs. Si tu veux, tu peux vérifier que l'expression de \dot{\theta}^{2} obtenue précédemment est conforme au théorème de l'énergie cinétique. Pour avoir la condition initiale permettant au pendule rigide d'effectuer un tour complet, il suffit de vérifier que l'expression de \dot{\theta}^{2} ne s'annule pas pour compris entre zéro et 2 rad.

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 22-01-21 à 22:28

Bonsoir,
pour déterminer la vitesse minimale \dot\theta_0 qui permet au pendule de faire un tour complet, je procède comme suit:

*on utilisant l'expression obtenu de \dot\theta^2:

\dot\theta^2=A e^{-a\theta} -  \frac{g}{R}(B.cos\theta+C.sin\theta)

\dot\theta^2(\theta=\pi)=Ae^{-a\pi}+\frac{g}{R}.B

*on utilise le théoreme de l'energie cinetique :

\Delta Ec=w(f)+w(p)

\frac{1}{2}mR^2\dot\theta^2(\theta=\pi)-\frac{1}{2}mR^2\dot\theta^2_0=-k\int_0^{\pi}v^2d\theta-\int_0^{\pi}mgR(1-cos(\theta))

=-k[A.\frac{1}{a}(1-e^{-a\pi})-\frac{g}{R}2C]-2mgR \\


pour un tour complet il faut que \dot\theta>0 à \theta=\pi
dans les deux méthode  la constante A contient la valeur \dot\theta_0
les calculs sont un peut plus long mais ils ne sont pas difficile  

je veux seulement poser la question
si la vitesse initiale est suffisante pour faire n tour

pour déterminer n  est ce q'on peut faire :

à \theta =0

\frac{1}{2}mR^2\dot\theta^2 ( \dot\theta pour  2n\pi)-\frac{1}{2}mR^2 \dot\theta_{min}^2 ( \dot\theta pour  un  tour)=-2\pi n. k\int_0^{2\pi}v^2d\theta

je veux aussi savoir si on peut utiliser cette formule pour démontrer la formule trouvé dans Wikipédia :



\frac{1}{1+4k^2}(1+e^{4nk\pi}e^{-2k\pi})<H<\frac{1}{1+4k^2}(1+e^{4nk\pi}e^{+2k\pi})

merci d'avance.







  

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 23-01-21 à 11:58

Il est possible de déterminer le nombre de tours effectués pour une valeur donnée de Vo. On peut imaginer la méthode suivante :

1° : déterminer la vitesse limite VoL de passage à l'équilibre stable en =0 en dessous de laquelle le pendule se met à osciller. Comme tu l'a fait remarquer, c'est la valeur pour laquelle la vitesse angulaire s'annule en = rad.

2° : puisque l'expression démontrée de \dot{\theta}^{2} reste valide tant que la vitesse angulaire ne change pas de signe, tu as :

instant initial : \frac{V_{o}^{2}}{R^{2}}=A-\frac{g.B}{R}=A+\frac{2g}{R.\left(1+a^{2}\right)}

Après un tour : \frac{V_{o1}^{2}}{R^{2}}=A.\exp\left(-2\pi.a\right)-\frac{g.B}{R}=A.\exp\left(-2\pi.a\right)+\frac{2g}{R.\left(1+a^{2}\right)}

Après n tours : \frac{V_{on}^{2}}{R^{2}}=A.\exp\left(-2\pi.n.a\right)-\frac{g.B}{R}=A.\exp\left(-2\pi.n.a\right)+\frac{2g}{R.\left(1+a^{2}\right)}

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 23-01-21 à 21:33

Bonsoir Vanoise,
merci pour cette explication,
donc si je comprend, pour determiner n
on fait
\frac{V_{on}^{2}}{R^{2}}}=A.\exp\left(-2\pi.n.a\right)+\frac{2g}{R.\left(1+a^{2}\right)}

avec V_{on}=  V_{oL}   ( la valeur pour laquelle la vitesse angulaire s'annule en \theta=\pi rad.)

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 23-01-21 à 22:40

C'est un peu moins restrictif que cela. Tu devrais tomber, comme sur le document que tu as cité, sur une double inégalité.
Après (n-1) tour le pendule a encore assez de vitesse pour effectuer encore un tour mais, après le nième tour, il n'a pas assez de vitesse pour en effectuer un autre.

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 26-01-21 à 19:33

Bonsoir,
J'arrive pas à résoudre le problème, mais quand même je vais débrouiller  avec le formule mentionné à Wikipédia pour le comprendre
il ont utiliser la formule de vitesse
\dot\theta^2=A'e^{a\theta}+B'cos (\theta)+C'Sin(\theta)
(Comme dans notre traitement)
Avec
a=2k (contraire à nous qui on a : a=-2\frac{kR}{m} mais il est un peu compatible avec le facteur trouvé dans les frottement solide, sauf le signe - qui se change selon le sens de mouvement , nous on peut faire un changement de variable

k'=\frac{kR}{m}  )  

B'=-2\frac{g}{R}.\frac{1}{1+a^2}  (comme dans notre traitement)

A'=-B'=2\frac{g}{R}.\frac{1}{1+4k'^2}

(nous on a A'=-B'+\dot\theta_0^2 ; A'=-B' n'est pas réaliser que dans le cas des condition initial : à   t=0     \theta=0     et     \dot\theta_0=0 )

Donc à \theta=0 on a pour n tour ; \theta=2n\pi

\dot\theta^2(pour  n-1  tour )< \dot\theta^2(pour  n  tour )< \dot\theta^2(pour  n+1  tour )

On a n+1 tour si le pendule effectue n tour et ajoute  un demi-tour  complète avec vitesse positive strictement  (si vitesse est strictement positive a \theta=\pi le pendule complète le tour)
Donc

\dot\theta^2(2n\pi-\pi)< \dot\theta^2(2n\pi)< \dot\theta^2(2n\pi+\pi)

Et puisque     Sin(2\pi(n-\frac{1}{2}))=0    et       cos(2\pi(n-\frac{1}{2}))=-1

\dot\theta^2(2n\pi-\pi)=A'e^{a(2n\pi-\pi) }-B'= A'(e^{2k'(2n\pi-\pi) }+1)
Et par suite

2\frac{g}{R}.\frac{1}{1+4k'^2}(e^{2k'(2n\pi-\pi) }+1)< \dot\theta^2(2n\pi)< 2\frac{g}{R}.\frac{1}{1+4k'^2}(e^{2k'(2n\pi-\pi) }+1)

Multipliant l'inégalité par \frac{R}{2g}
On trouve

\frac{1}{1+4k'^2}(e^{2k'(2n\pi-\pi) }+1)< H'<\frac{1}{1+4k'^2}(e^{2k'(2n\pi-\pi) }+1)
La formule de Wikipédia avec:

H'=\frac{R}{2g}\dot\theta^2(2n\pi)

Or Wikipédia utilise  H=R^2\dot\theta^2+2gR(1-cos(\theta))= R^2\dot\theta^2 car \theta=0
Ce qui nous donne H=2Rg.H'

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 26-01-21 à 22:09

je m'excuse le 3ème terme de l'inéquation est



2\frac{g}{R}.\frac{1}{1+4k'^2}(e^{2k'(2n\pi+\pi) }+1)

Multipliant l'inégalité par \frac{R}{2g}
On trouve :

\frac{1}{1+4k'^2}(e^{2k'(2n\pi+\pi) }+1)

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 27-01-21 à 12:42

Changer les notations : cela finit par être perturbant. Je conserve donc celle définies dans ton message du 19-01-21 à 20:58 et reprises dans mon message du 23-01-21 à 11:58.
Concernant ton dernier message, il y a un problème sur le sens des inégalités  :

\dot{\theta}^{2}(pour\;n-1\;tour)>\dot{\theta}^{2}(pour\;n\;tour)>\dot{\theta}^{2}(pour\;n+1\;tour)

De plus, cela n'est vrai que pour des valeurs identiques de modulo 2 car le travail de la force de pesanteur intervient quand on compare les vitesses à des altitudes différentes. En cas de tours complets, la vitesse est donc nettement plus élevée en \theta=2n.\pi qu'en \theta=2n.\pi\mp\pi. L'inégalité suivante est donc fausse :

\color {red}}{\dot{\theta}^{2}(2n\pi-\pi)<\dot{\theta}^{2}(2n\pi)<\dot{\theta}^{2}(2n\pi+\pi)}   FAUX !

Je reprends donc mon raisonnement du 23-01-21 à 11:58

La vitesse VoL correspond à une vitesse nulle en \theta=\pi :

A=\frac{V_{o}^{2}}{R^{2}}-\frac{2g}{R.\left(1+a^{2}\right)}

En \theta=\pi :

0=\left[\frac{V_{oL}^{2}}{R^{2}}-\frac{2g}{R.\left(1+a^{2}\right)}\right]\exp\left(-a.\pi\right)-\frac{2g}{R.\left(1+a^{2}\right)}

Après simplifications :

\frac{V_{oL}^{2}}{R}=\frac{2g}{1+a^{2}}\left[1+\exp\left(a.\pi\right)\right]

Remarque : tu peux vérifier au passage que le cas particulier a=0 correspond bien à la valeur de VoL obtenue en absence de frottement pour un pendule rigide.

Pour que le pendule rigide puisse effectuer n tours, il doit avoir en \theta=2\pi\left(n-1\right) une vitesse supérieure à VoL mais avoir en \theta=2\pi n une vitesse inférieure à VoL :

\left[\frac{V_{o}^{2}}{R^{2}}-\frac{2g}{R.\left(1+a^{2}\right)}\right].\exp\left[-2\pi.a.\left(n-1\right)\right]+\frac{2g}{R.\left(1+a^{2}\right)}>\frac{2g}{R.\left(1+a^{2}\right)}\left[1+\exp\left(a.\pi\right)\right]>\left[\frac{V_{o}^{2}}{R^{2}}-\frac{2g}{R.\left(1+a^{2}\right)}\right].\exp\left[-2\pi.a.n\right]+\frac{2g}{R.\left(1+a^{2}\right)}

Il y a des simplifications bien sûr...

Calculs à vérifier. Je ne suis pas à l'abri d'une erreur ou étourderie dans l'utilisation de l'éditeur d'équations.

Posté par
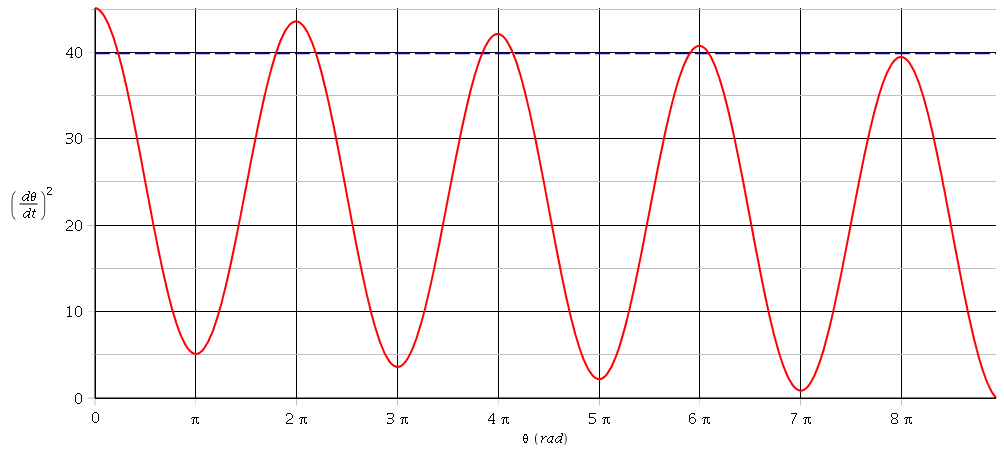
vanoisere : mouvement dans un trajet circulaire avec frottement 28-01-21 à 15:17

Voici une simulation illustrant mon précédent message. J'y ai représenté les variations en fonction de du carré de la vitesse angulaire pour une valeur de Vo un peu supérieure à VoL : Vo=1,064VoL pour être précis. J'ai choisi a=0,01. L'ordonnée de l'horizontale en pointillés bleus correspond à \frac{V_{oL} ^2}{R^2}. (graduations de l'axe des ordonnées arbitraires). Deux remarques :
1° : On voit bien que la cause principale des variations de \dot{\theta}^{2} est la variation d'altitude :  les valeurs sont toujours nettement plus élevée en positions hautes qu'en positions basses.
2° : On remarque que, au bout de 3 tours, la vitesse en =6 est un peu supérieure à la valeur limite permettant d'effectuer un quatrième tour mais que la vitesse en =8 n'est pas suffisante pour effectuer un cinquième tour. Le pendule rigide effectue ainsi 4 tours complets. Sa vitesse s'annule un peu avant la position haute suivante (en =8,9 rad). Il se met alors à osciller. Je n'ai pas étudié ici  les oscillations amorties...

mouvement dans un trajet circulaire avec frottement

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 29-01-21 à 20:56

Merci vanoise,
Merci pour l'explication,
Merci pour la correction
je sais d'avance que mon message précédent est plein d'erreur, mais je veux quand meme le poster pour la correction, merci pour vos efforts avec moi.

j'ai deux derniere question pour terminer ce sujet:

1- dans la phase oscillatoire est ce qu'on peut savoir le nombre d'osscillation avat que le pendule s'arrette

2- dans le cas de faible amplitude (sin(\theta)=\theta

l'equation de mouvement :

\ddot{\theta} +\frac{k.R}{m}\dot{\theta}^2+\frac{g}{R}.\theta=0

avoir une solution

*pour la 1ère question je propose qu'on dénombrer les \theta_m entre le premier \theta_m et 0. mais le problème on ne peut pas déterminer une solution littérale à l'équation    \dot\theta^2=0
je sais pas d'abord si c'est un nombre fini ou on a seulement     \theta_m     tend vers 0 quand t tend vers l'infini

*pour la deuxième question j'ai aucun idée

Posté par
vanoisere : mouvement dans un trajet circulaire avec frottement 30-01-21 à 12:26

Citation :
dans la phase oscillatoire est ce qu'on peut savoir le nombre d'osscillation avat que le pendule s'arrette

N'oublie pas que le sens de la force de frottement change à chaque fois que la vitesse angulaire change de signe. Un peu comme cela a été fait pour les frottements solides, il faut donc étudier successivement le mouvement vers la droite puis le mouvement vers la gauche en changeant le signe de la force de frottement. On pourra ainsi obtenir les amplitudes successives après une demie pseudo période, deux demies pseudo périodes et ainsi de suite. Ces amplitudes successives font intervenir e-a.. Cette valeur tend vers zéro quand augmente. Tu as donc fourni la réponse : "on a seulement     \theta_m     tend vers 0 quand t tend vers l'infini." On peut obtenir  une solution approchée réaliste en posant e-a.=0 pour a.>5. Cette méthode est très souvent utilisée en physique chimie : durée de la charge d'un condensateur par exemple. Je rappelle l'écriture correcte de l'équation différentielle :

\ddot{\theta}+\frac{k}{m}\dot{\theta}.|\dot{\theta}|+\frac{g}R}\cdot\sin(\theta)=0
Dans le cas des faibles amplitudes, l'équation différentielle s'écrit :

\ddot{\theta}+\frac{k}{m}\dot{\theta}.|\dot{\theta}|+\frac{g}{R}\cdot \theta=0
Pas de solution littérale simple à ma connaissance. Il faut se contenter d'une simulation numérique.

Posté par
prafre : mouvement dans un trajet circulaire avec frottement 31-01-21 à 20:50

Bonsoir,
Merci Vanoise,
Je te remercie pour votre aide , votre effort et votre patience
Votre aide m'a beaucoup soutenu
grâce a vous, j' ai pu traiter et résoudre le sujet qui me poser un grand difficulté
surtout ce sujet est rarement été traité dans les ouvrages physique et même sur le net

merci beaucoup

1 2 3 +


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !