Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie

1 2 +

Niveau licence
Partager :

Mouvement avec vitesse initial dans un plan horizontal

Posté par
praf 13-11-23 à 21:06

Bonsoir les amis.
un exercice que je le trouve très difficile.
votre aide s'il vous plaît.

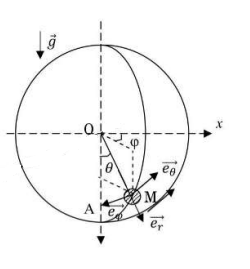
On considère un palet assimilable à un point matériel M de masse m au fond d'une cuvette sphérique de rayon R=1m. le champ de gravité de norme g, est vertical descendant. Les frottements sont négligeables.
Le palet est enfin lancé d'une position caractérisée par \theta_0
Avec une vitesse initial horizontale tangente à la sphère, de valeur V_0.
Le mouvement n'est plus plan (sauf pour une vitesse initiale que l'on va cherchera)
Le repère adapté est le repère local des cordonné sphérique
(O,\overrightarrow{e_r},\overrightarrow{e_{\theta}},\overrightarrow{e_{\phi}})  et {v(0)}=v_{0 \overrightarrow{e_{\phi}}} \\
on donne l'expression de la vitesse et l'accélération en coordonné sphérique:

V=\dot{r}.\overrightarrow{e_r} +r.\dot{\theta}.\overrightarrow{e_{\theta}} +r. sin(\theta).\dot{\phi}.\overrightarrow{e_{\phi}}

\overrightarrow{a}=(\ddot{r}+r.\dot{\theta}^2+r. sin^2(\theta).\dot{\phi}^2)\overrightarrow{e_r} +(2\dot{r}.\dot{\theta}+r.\ddot{\theta}-r.sin(\theta).cos(\phi)).\dot{\phi}^2)\overrightarrow{e_{\theta}} \\ +(\frac{1}{r. sin(\theta)}.\frac{d}{dt}(r^2. sin(\theta)^2.\dot{\phi})).\overrightarrow{e_{\phi}} \\


1- Montrez que la quantité sin^2(\theta). \dot{\phi} est une constante de mouvement.
Donner la valeur de cette constante en fonction des conditions initiales.

2- Montrer que l'énergie mécanique est une constante de mouvement.
Donner la valeur de cette constante en fonction des conditions initiales.

3- Déduire de la conservation de E_m que \theta est une solution de l'équation

\dot{\theta}^2=f(\theta)=[\frac{v_0^2}{R^2}(1-\frac{\sin^2(\theta_0)}{sin^(\theta)}) + \frac{2.g}{R}.(cos \theta - cos \theta_0)]

4- On souhaite montrer qu'il existe une valeur particulière v_3 de v_0 pour lequel le mouvement est circulaire uniforme dans le plan \theta (t)=\theta_0
Pour cela on pose u=cos(\theta).
Réécrire l'équation f(\theta) de sorte que :

f(\theta)=f(u)=\frac{P(u)}{1-u^2}

ou P(u) est une fonction polynomiale de degré 3 par rapport à u, à expliciter.
Montrer que P(u) n'admet que deux racines réelles dans l'intervalle] -1,1[dont l'une au moins est égale à   u_0  
Montrer que si   u_0  est une racine double, le mouvement est circulaire uniforme dans le plan \theta(t)=\theta_0.
En déduire la valeur de v_3

5- Décrire le mouvement pour v_0>v_3. On raisonnera qualitativement et on vérifiera la prévision par l'analyse de P(u)

Mouvement avec vitesse initial dans un plan horizontal

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 13-11-23 à 21:06

pour la 1ere question je pense de faire \frac{d}{dt}( sin^2(\theta). \dot{\phi}) si égale à 0 c'est une constante de mouvement
Je trouve (si je ne trompe pas)
\frac{d}{dt}( sin^2(\theta). \dot{\phi})=\dot{\theta}.sin(2. \theta). \dot{\phi}+sin^2(\theta). \ddot{\phi}
Et je me bloque

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 13-11-23 à 21:30

Bonjour
As-tu pensé à appliquer la relation fondamentale de la dynamique ?

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 13-11-23 à 21:35

bonsoir Vanoise,
Merci pour votre aide
est la relation fondamentale de dynamique pour la 1ère question
c-à-d pour montrer la constante de mouvement

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 13-11-23 à 21:42

praf @ 13-11-2023 à 21:35

bonsoir Vanoise,
Merci pour votre aide
est ce que la relation fondamentale de dynamique pour la 1ère question?
c-à-d pour montrer la constante de mouvement

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 13-11-23 à 21:43

Que peux-tu dire de la composante de l'accélération selon e ?

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 13-11-23 à 21:48

est ce qu'on peut dire qu"il est nulle ? je prétend. je ne suis pas sur. car le mouvement n'est pas uniforme.

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 13-11-23 à 21:52

Quelles sont les deux forces appliquées en absence de frottement ? Leurs composantes selon e ?

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 13-11-23 à 21:58

je pense on a le poids et la force centrale
leur composant selon
pour le poids c'est nul car le poids est verticale

pour la force centrale : je pense par analogie avec le mouvement circulaire horizontale c'est   m.\frac{v^2}{r}

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 13-11-23 à 22:03

Pas vraiment.
En absence de frottement la réaction de la cuvette est centrale, dirigée suivant -er. Le poids est vertical et n'a donc pas de composante selon e.
Conclusion ? L'énoncé fournit l'expression générale de l'accélération...

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 14-11-23 à 20:21

bonsoir Vanoise.
je fait un test:

les deux forces appliquées en absence de frottement:
le poids : \overrightarrow{P}
l'action de la sphère :  \overrightarrow{R} qui est normale en absence de frottement

la relation fondamental de dynamique :
\overrightarrow{P}+\overrightarrow{R}=m.\overrightarrow{a}
projecton cette relation :
on a :
\overrightarrow{P} (m.g.cos(\theta), m.g.sin(\theta), 0)  (je ne suis pas sur pour \overrightarrow{e_{\theta}})
\overrightarrow{R} (0, R, 0)  ( je ne suis pas sur pour \overrightarrow{e_{r}})

donc pour \overrightarrow{e_{\phi}} :
0=m. (\frac{1}{r. sin(\theta)}.\frac{d}{dt}(r^2. sin(\theta)^2.\dot{\phi}))

c-à-d :  \frac{d}{dt}(r^2. sin(\theta)^2.\dot{\phi})=0

c-à-d :  r^2. sin(\theta)^2.\dot{\phi}=cst
on a r est constante
donc sin(\theta)^2.\dot{\phi} est constante

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 14-11-23 à 22:39

Juste quelques remarques :
* Pas trop astucieux de noter \vec R la réaction de la piste puisque la lettre R est réservée par l'énoncé au rayon de la piste.
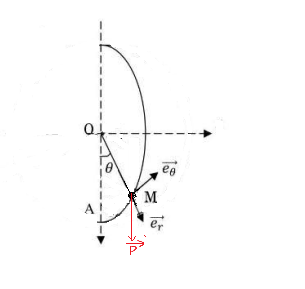
* La démonstration nécessite seulement de vérifier que la résultante des forces n'a pas de composante selon \vec{e_{\varphi}}. Pas nécessaire d'expliciter les composantes non nulles dans la mesure où l'exploitation des équations différentielles qui résultent de la RFD ne peut se faire que par simulation numérique informatisée et n'est donc pas demandée ici. Si tu veux le faire, tu as tout intérêt à faire une figure propre avec comme plan de figure le plan (OAM) perpendiculaire à \vec{e_{\varphi}} . La figure est ainsi très analogue à celle correspondant à un pendule simple.
* Tout à fait d'accord avec ta démonstration conduisant à \dot{\varphi}.\sin^{2}\left(\theta\right)=constante .

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 19:04

Bonsoir Vanoise.
merci pour votre aide.
c'est juste que la question ne demande pas les composant de  poids : \overrightarrow{P} et la réaction de la sphère : \overrightarrow{T}
dans le repère de coordonné sphérique. mais moi j'exploite le moment pour bien comprendre ce traitement.


donc le résultat proposé dans mon message précédent et faut

si on considère le plan (OAM)  perponduculaire  à \vec{e_{\varphi}} :

\vec{e_{\theta}} et \vec{e_r}  est perponduculaire dans le plans (OAM)

\vec{e_r} est collinieaire à (OM) :

\vec{P} =(R.cos \theta , R.sin \theta , 0)

\vec{T}= (T, 0, 0)

la valeur de T se détermine par l'application de la relation fondamentale de dynamique

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 19:08

je m'excuse. je trompe pour  \vec{P}

on a :

\vec{P} =(m.g.cos \theta, m.g.sin \theta, 0)

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 19:24

Problème double de signe.
1 : la réaction de la piste sphérique est centripète alors que \vec e_r est centrifuge.
2 : signe de la composante du poids selon \vec e_\theta à revoir.

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 19:26

As-tu fait une figure comme conseillé dans mon message du 14-11-23 à 22:39 ?

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 19:54

Merci Vanoise.
je fait une figure, mais j'ai mal représenter \vec{e_{\theta}} à cause de concevoir le repère direct
je pense que :
dans le plan (OAM)
\vec{e_{\theta}} se dirige vers le haut tangente avec la sphère
et \vec{e_{\varphi}} est perpendiculaire au plan se dirige vers la gauche :
et par suite :




\vec{P} =(m.g.cos \theta, - m.g.sin \theta, 0)

\vec{T}= (-T, 0, 0)

Mouvement avec vitesse initial dans un plan horizontal

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 20:55

La trace de la piste dans le plan de figure est un cercle. Tout le reste est bon.

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 21:03

Merci beaucoup Vanoise.
pour la question :
Donner la valeur de cette constante en fonction des conditions initiales.  

on a à t=0 \theta(t=0)=\theta_0
et
\dot \varphi (t=0) ={v(0)}=v_{0 \overrightarrow{e_{\phi}}}
danc la constante de mouvement = \theta_0 . v_0

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 21:10

Une vitesse angulaire ne peut être égale à une vitesse !

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 21:13

Pour t'aider : pars de l'expression générale du vecteur vitesse et adapte la aux conditions initiales.

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 21:15

oui. exactement
donc on doit diviser la par R
et par suite :
on \dot \varphi (t=0)= \frac{v_0}{R}

la constante de mouvment = \theta_0 . \frac{v_0}{R}

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 21:19

Non : le rayon de la trajectoire circulaire horizontale n'est pas égale à R.

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 21:30

si on utilise l'expression :
V=\dot{r}.\overrightarrow{e_r} +r.\dot{\theta}.\overrightarrow{e_{\theta}} +r. sin(\theta).\dot{\phi}.\overrightarrow{e_{\phi}} \\

on a V(t=0)=v_{0 \overrightarrow{e_{\varphi}}} = r. sin(\theta).\dot{\phi}.\overrightarrow{e_{\phi}}

sin(\theta).\dot{\phi}.\overrightarrow{e_{\phi}}=\frac{v_0}{r}=\frac{v_0}{R.sin \theta}

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 21:31


je m'excuse

sin(\theta).\dot{\phi}.\overrightarrow{e_{\phi}}=\frac{v_0}{r_0}=\frac{v_0}{R.sin \theta_0}

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 21:56

C'est la constante \dot{\varphi}.\sin^{2}\left(\theta\right) qu'il faut exprimer en fonction de R, vo et o.

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 15-11-23 à 22:32

Oui exactement.
j'y reflechi

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 16-11-23 à 19:50

Bonsoir Vanoise.

on a
  \theta(t=0)=\theta_0 et r_0=R.sin(\theta_0)

V(t=0)=v_{0 \vec{e_{\varphi}}} = r_0. sin(\theta_0).\dot{\varphi}(0).\vec{e_{\phi}}
c-à-d :

v_{0 } = r_0. sin(\theta_0).\dot{\varphi}(0)

c-à-d :

\dot{\varphi}.\sin^{2}\left(\theta\right) = \dot{\varphi}(0).\sin^{2}\left(\theta_0\right) =\frac{v_0.sin(\theta_0)}{r_0}=\frac{v_0.sin(\theta_0)}{R.sin(\theta_0)}=\frac{v_0}{R}

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 16-11-23 à 20:13

Je n'ai pas tout à fait cela. Déjà obtenu :

v_{o}=R.\dot{\varphi_{o}}.\sin\left(\theta_{o}\right)\quad soit\quad\dot{\varphi_{o}}=\frac{v_{o}}{R.\sin\left(\theta_{o}\right)}

D'où l'expression de la constante du mouvement :

K=\dot{\varphi}.\sin^{2}\left(\theta\right)=\dot{\varphi}_{o}.\sin^{2}\left(\theta_{o}\right)=\frac{v_{o}}{R.\sin\left(\theta_{o}\right)}\cdot\sin^{2}\left(\theta_{o}\right)

A retenir pour la suite :

\dot{\varphi}=\dfrac{v_{o}}{R}\cdot\dfrac{\sin\left(\theta_{o}\right)}{\sin^{2}\left(\theta\right)}

A noter pour la suite une étourderie dans la copie de la formule sur f() : sin() doit apparaître au carré. Il y a aussi une erreur dans l'expression de la composante de l'accélération suivant \overrightarrow{e_{\theta}} mais cela est sans conséquence .

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 16-11-23 à 20:32

Merci Vanoise
il y a encore confusion pour moi entre r et R
au début moi je confondre entre R et r parce que le mouvement reste sur la sphère mais ton message 15-11-23 à 21:19 ma perturber mon idée.
r et le rayon de la trajectoire circulaire et pas R

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 16-11-23 à 20:34

r est le rayon de la trajectoire circulaire et n'est pas R

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 16-11-23 à 20:58

pour les faute dans le tapage des expression. c'est vrai
je recopier les formule une autre fois.


\\ \vec{a}=(\ddot{r}-r.\dot{\theta}^2-r. sin^2\theta .\dot{\varphi}^2)\vec{e_r} +(2\dot{r}.\dot{\theta}+r.\ddot{\theta}-r.sin \theta.cos \theta .\dot{\varphi}^2)\ver{e_{\theta}} \\ \\   +(\frac{1}{r. sin \theta}.\frac{d}{dt}(r^2. sin^2\theta.\dot{\varphi})).\vec{e_{\varphi}}


\dot{\theta}^2=f(\theta)=[\frac{v_0^2}{R^2}(1-\frac{\sin^2\theta_0}{sin^2\theta}) + \frac{2.g}{R}.(cos \theta - cos \theta_0)]

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 16-11-23 à 21:06

D'accord maintenant !

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 16-11-23 à 21:12

pour la 2ème question
on a E_m= E_p+E_c
\\ E_p= m.g.R.(1-cos \theta_0)
\\ E_c= \frac{1}{2}m.v^2
mais comment obtenir v^2

c'est clair que E_m est une constante de mouvement car les force est conservatives ( il n y a pas de frottement)

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 16-11-23 à 21:56

Le plus direct pour obtenir le résultat demandé consiste à écrire que Em à un instant quelconque est égale à Em à l'instant de date zéro.
L'énoncé fournit l'expression de la vitesse donc...
La fin de mon précédent message est importante...

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 17-11-23 à 12:29

bonjour :
on a


V=\dot{r}.\vec{e_r} +r.\dot{\theta}.\vec{e_{\theta}} +r. sin(\theta).\dot{\varphi}.\vec{e_{\varphi}}

je n'est pas sur, mais il me semble que :

\\ v^2=\dot{r}^2 +r^2.\dot{\theta}^2 +r^2. sin(\theta)^2.\dot{\varphi}^2

\dot{r}=0  et   \dot{\theta}(t=0)=0

\\ \dot{\varphi}^2(t=0)=\dfrac{v_{o}}{R}\cdot\dfrac{1}{\sin\left(\theta_0\right)}

et par suite :

v^2=R^2.sin\theta_0.\dfrac{v_{o}}{R}\cdot\dfrac{1}{\sin\left(\theta_0\right)}

c-à-d

v^2 =R.v_0

et

E_m= m.g.R.(1-cos \theta_0)+\frac{1}{2}m.R.v_0

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 17-11-23 à 13:53

Citation :
v^2 =R.v_0

Un carré de vitesse égal au produit d'une vitesse par une distance ??? Toujours vérifier l'homogénéité des formules obtenues : cela permet d'éviter des erreurs grossières jugées impardonnables par un jury de concours ou d'examen.

Il ne faut pas confondre ce qui est valide à t=0 et ce qui est valide à un instant quelconque.

Énergie mécanique initiale :

E_{mo}=\frac{1}{2}m.v_{o}^{2}+m.g.R.\left[1-\cos\left(\theta_{o}\right)\right]

À un instant quelconque :

E_{p}=m.g.R.\left[1-\cos\left(\theta\right)\right] \\ \\ E_{c}=\frac{1}{2}m.R^{2}.\dot{\theta}^{2}+\frac{1}{2}m.R^{2}.\sin^{2}\left(\theta\right).\dot{\varphi}^{2}

C'est maintenant qu'interviennent les résultats des questions précédentes rappelés dans mon message du 16-11-23 à 20:13 :

\dot{\varphi}=\dfrac{v_{o}}{R}\cdot\dfrac{\sin\left(\theta_{o}\right)}{\sin^{2}\left(\theta\right)}

D'où l'expression de Ec :

\\ E_{c}=\frac{1}{2}m.R^{2}.\dot{\theta}^{2}+\frac{1}{2}m.R^{2}.v_{o}^{2}\cdot\dfrac{\sin^{2}\left(\theta_{o}\right)}{\sin^{2}\left(\theta\right)}

Écrire : Emo=Em=Ec+Ep conduit à la relation demandée.

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 17-11-23 à 18:14

Moi qui parlais des fautes d'homogénéité, je viens d'en laisser passer une belle en recopiant ma dernière formule. Je corrige :

D'où l'expression de Ec :


\\ E_{c}=\frac{1}{2}m.R^{2}.\dot{\theta}^{2}+\frac{1}{2}m.v_{o}^{2}\cdot\dfrac{\sin^{2}\left(\theta_{o}\right)}{\sin^{2}\left(\theta\right)}

Écrire : Emo=Em=Ec+Ep conduit à la relation demandée.

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 17-11-23 à 19:47

merci beaucoup Vanoise
maintenant on peut faire

E_c+E_p=E_m0



\frac{1}{2}m.R^{2}.\dot{\theta}^{2}+\frac{1}{2}m.v_{o}^{2}\cdot\dfrac{\sin^{2}\left(\theta_{o}\right)}{\sin^{2}\left(\theta\right)}+m.g.R.\left[1-\cos\left(\theta\right)\right]=\frac{1}{2}m.v_{o}^{2}+m.g.R.\left[1-\cos\left(\theta_{o}\right)\right]

\frac{1}{2}m.R^{2}.\dot{\theta}^{2}=\frac{1}{2}m.v_{o}^{2}-\frac{1}{2}m.v_{o}^{2}\cdot\dfrac{\sin^{2}\left(\theta_{o}\right)}{\sin^{2}\left(\theta\right)}-m.g.R.\left[1-\cos\left(\theta\right)\right]+m.g.R.\left[1-\cos\left(\theta_{o}\right)\right]

facilement on peut tirer :

\dot \theta^2=\dfrac{v_{0}^{2}}{R^2} (1-\dfrac{\sin^{2}\left(\theta_{o}\right)}{\sin^{2}\left(\theta\right)}) + \dfrac{2.g}{R}(\cos\left(\theta\right)\right-\cos\left(\theta_{o}\right)\right))

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 17-11-23 à 19:50

Ok. C'est ensuite que la situation se complique un peu...

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 17-11-23 à 20:12

si on pose u = cos (\theta)

on a sin^2(\theta)= 1-u^2

et p(u)=-\frac{2.g}{r}.u^3-(\frac{2.g}{R}-\frac{v_0^2}{R^2})u^2+\frac{2.g}{R}.u+(\frac{v_0^2}{R^2}.cos^2(\theta_0)-\frac{2.g}{R}.cos(\theta_0))

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 17-11-23 à 20:59

Petit conseil pour faciliter la suite : écrire le polynôme sous la forme :
P(u)=(u-uo).Q(u)
Pour obtenir v3, il suffira alors de trouver la condition sur la vitesse initiale pour que soit vérifiée :
Q(uo)=0.

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 17-11-23 à 21:15

merci Vanoise.
je vais essayer

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 18-11-23 à 19:25

bonsoir :
je tiens de corrigé une petite faute dans p(u) dans mon message précedent :

P(u)= -\dfrac{2.g}{R}.u^3 + u^2(-\dfrac{v_0^2}{R^2}+\dfrac{2.g}{R}.u_0) + \dfrac{2.g}{R}.u + \dfrac{v_0^2}{R}u_0^2-\dfrac{2.g}{R}u_0)

P(u)=(u-u_0)Q(u)

avec Q(u)=au^2+bu+c

on a :

a=-\dfrac{2.g}{R}        ;      b=\dfrac{v_0^2}{R^2}   ;         c=\dfrac{2.g}{R}-\dfrac{v_0^2}{R^2}.u_0

déscriminant de Q(u)

\Delta=\dfrac{v_0^4}{R^4}+\dfrac{16.g^2}{R^2}-\dfrac{8.g}{R^3}v_0.u_0 \\
on a :

\Delta=\dfrac{1}{R^2}[(\dfrac{v_0^2}{R}-4.g.u_0)^2+16.g^2(1-u_0^2)]

\Delta>0    car     u_0<1

donc deux solution  :


u_1=\dfrac{-v_0^2+\sqrt{(\dfrac{v_0^2}{R}-8.g.u_0)\dfrac{v_0^2}{R}+16.g^2}}{2.g}


u_1=\dfrac{-v_0^2-\sqrt{(\dfrac{v_0^2}{R}-8.g.u_0)\dfrac{v_0^2}{R}+16.g^2}}{2.g}

Posté par
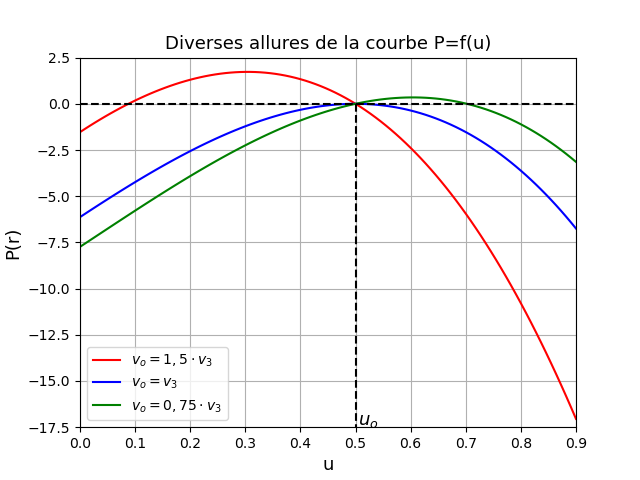
prafre : Mouvement avec vitesse initial dans un plan horizontal 18-11-23 à 19:26

la deuxième solution est  : u_2

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 18-11-23 à 20:01

D'accord avec ton expression de Q(u). Pour éviter les fractions, j'ai étudié les racines de R2.Q(u). Logiquement, une des racine est largement inférieure à -1 et n'a pas de sens physique. Pour t'aider, voici  les allures possibles de P(u) suivant les valeurs de vo. Bien sûr uo est une racine et l'autre racine comprise entre zéro et 1 est, soit supérieure à uo, soit inférieure à uo selon que vo est inférieure, égale ou supérieure à v3. Pour tracer les courbes, j'ai choisi, de façon arbitraire : R=1m ; o=/3 rad.
A noter que, sans faire tous ces calculs, la valeur de v3 peut être obtenue en deux lignes si on a en tête la théorie du pendule conique.

Mouvement avec vitesse initial dans un plan horizontal

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 18-11-23 à 20:13

qu'est ce que je doit faire maintenant ?

déterminer la deuxième racine différent de u0 ?

Posté par
vanoisere : Mouvement avec vitesse initial dans un plan horizontal 18-11-23 à 20:19

Il faut étudier la condition sur vo permettant d'obtenir une racine double et étudier le mouvement dans ce cas particulier. Approfondissement possible non demandé par l'énoncé : vérifier que le résultat est cohérent avec l'étude simple du pendule conique.

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 18-11-23 à 20:23

Merci je vais essayer les calculs.

racine double ça veut dire \Delta=0

donc on doit déterminer la valeur de v_0 qui annule \Delta

Posté par
prafre : Mouvement avec vitesse initial dans un plan horizontal 18-11-23 à 20:28

je trompe
on pose Q(u_0)=0 et résoudre l'équation obtenu en v_0

1 2 +


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !