Inscription / Connexion Nouveau Sujet
moteur_synchrone
Bonsoir,
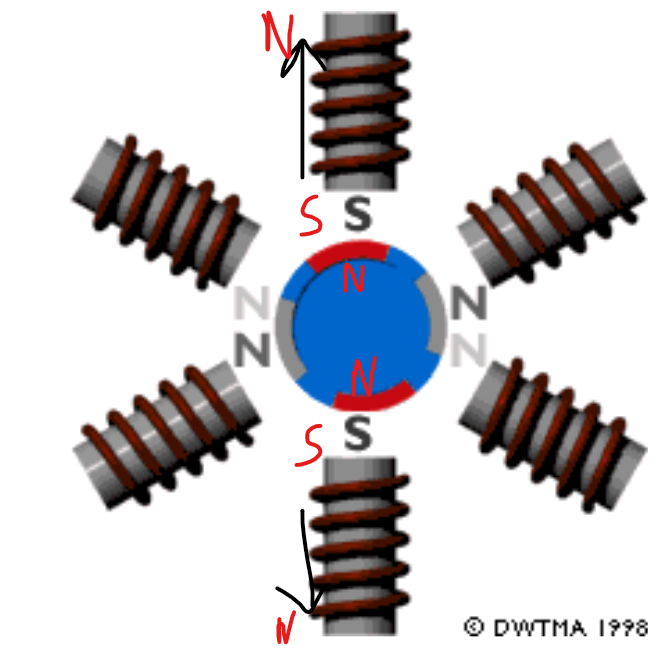
1) Je ne comprends pas le champ tournant crée par un moteur avec deux paires de poles ou plus. Je sais que l'on a 6 bobines, 2 bobines alimentés avec une phase. Mais après je n'arrive pas à m'imaginer comment tourne un rotor à aimant permanent.
A t-on pour 2 bobines alimentés par la même phase, un champ magnétique opposé ? (voir photo)
2) Nous avons en TP, utilisé les équations en magnétostatique pour modéliser la machine synchrone; sujet : https://www.ilephysique.net/sujet-machine-synchrone-ideale-323951.html#msg2617567
Avons nous fait cela car on ne s'intérèsse qu'à 1 instant du champ tournant ?
3) Enfin, on a vu que l'on doit résoudre
Cependant pour trouver cela, on doit dire que Rot B = 0
(Rot B = Rot rot A = grad div A -
or nous avons un courant présent sur la machine (voir sujet).
D'ailleurs on dira que div A = 0 avec la condition de jauge de Coulomb, je ne vois pas trop ce que c'est ...
Merci beaucoup !
Bonsoir
Je t'ai déjà répondu à propos du moteur synchrone triphasé dont le stator contient 3 bobines décalées d'un tiers de tour et alimentées par trois courants triphasés équilibrés.Tu obtiens un champ magnétique de norme fixe tournant à la vitesse angulaire 
. :
voir ici :
Moteur synchrone schéma
On obtient, dans un repère adéquat :
Imagine que tu ajoutes dans le stator trois bobines identiques aux précédentes, alimentées de la même façon mais décalées de 1/6 de tour. Dans le même repère, tu va obtenir un deuxième champ tournant de même norme mais dont les composantes sont déphasées par rapport aux premières de 
/3. Le signe dépend de la façon dont se fait le décalage.
Je te laisse exprimer la somme des deux vecteurs champ : tu vas obtenir un vecteur de norme constante tournant à la vitesse angulaire 2.
J'obtiens donc :
Il y a surement un problème car je ne vois pas le terme en 2w...
La disposition est donc comme sur la photo.
Oublie la deuxième partie de mon message précédent. Les bobines ne sont pas alimentées comme je l'ai écrit mais plutôt comme indiqué ici de façon à créer un champ tournant de vitesse angulaire /2. Désolé !
L'équation de Poisson s'écrit dans le cas général :
(attention : il s'agit d'un laplacien vectoriel, pas du laplacien d'un vecteur, ce qui n'aurait pas de sens).
L'équation simplifiée que tu écris s'applique en tout point où la densité de courant est nulle ; elle ne suppose pas l'absence de courant au voisinage des points où elle s'applique. En pratique, elle s'applique donc dans le vide au voisinage des bobines parcourues par des courants.
L'équation de Poisson s'écrit dans le cas général :
(attention : il s'agit d'un laplacien vectoriel, pas du laplacien d'un vecteur, ce qui n'aurait pas de sens).
L'équation simplifiée que tu écris s'applique en tout point où la densité de courant est nulle ; elle ne suppose pas l'absence de courant au voisinage des points où elle s'applique. En pratique, elle s'applique donc dans le vide au voisinage des bobines parcourues par des courants.
D'ailleurs on dira que div A = 0 avec la condition de jauge de Coulomb, je ne vois pas trop ce que c'est
Le potentiel vecteur est défini de sorte que le vecteur B vérifie :
Cela ne définit pas le potentiel vecteur de façon unique mais seulement à un gradient près puisque le rotationnel d'un gradient est nécessairement le vecteur nul. Pour lever l'ambigüité, on introduit une condition arbitraire supplémentaire dite condition de jauge. Ainsi, le potentiel vecteur est défini à un vecteur constant près, un peu comme le potentiel électrostatique qui est défini à une constante arbitraire près.
Merci,
Pour le lien, je ne vois pas trop donc pour le champ magnétique, ya t'il un moyen de démontrer le champ à vitesse w/2 ?
Pour la relation du laplacien, comment peut elle prendre en compte les courants à proximité sans le j, car ceux-ci influent sur A ?
Div A = 0 : donc ce qui arrive = ce qui part ainsi A n'est plus défini à un gradient près et est constant ?
Car sinon B serait toujours nul
Enfin, pourquoi considère t on en magnétostatique le système ?
Merci !!
Div A = 0 : donc ce qui arrive = ce qui part ainsi A n'est plus défini à un gradient près et est constant ?
Remplacer le vecteur A par un vecteur de la forme
Il existe donc a priori une infinité de potentiels vecteurs différents qui conviendraient puisqu'ils conduiraient tous au même vecteur champ B. Pour restreindre les possibilités, on impose arbitrairement une condition particulière : la condition de jauge :
On peut ensuite démontrer que cette expression du potentiel vecteur convient car son rotationnel conduit bien à l'expression du vecteur B donnée par la loi de Biot et Savart.
Bien sûr, ajouter au potentiel vecteur un vecteur constant C ne changerait pas l'expression du vecteur B puisque :
Ces équation sont valables en magnétostatique (champs indépendants du temps) et , en bonne approximation, en régimes lentement variables. En régime très haute fréquence, il faut faire intervenir les équations de Maxwell que tu étudieras plus tard.
Pour la relation du laplacien, comment peut elle prendre en compte les courants à proximité sans le j, car ceux-ci influent sur A ?
Je ne suis pas sûr que tu aies bien compris le cours sur les opérateurs... Prenons l'exemple du potentiel vecteur :
Dans cette expression, les variables d'intégrations sont les coordonnées de P, le point M étant considéré comme fixe. La densité de courant dans la source ( les fils d'une bobine par exemple) doit donc ne pas être le vecteur nul mais la densité de courant en M, à l'extérieur des fils de la bobine est nulle :
Or, en absence de précision contraire, les variables de dérivation qui interviennent dans les opérateurs (gradient, divergence, laplacien, rotationnel) sont les coordonnées de M, le point où on étudie le champ. Donc en M, point à l'extérieur des fils de la bobine :
Merci,
Du coup c'est pour cela que l'on reste en magnétostatique, car les équations utilisées ne sont valides que dans ce cas.
Dans le premier cas, le potentiel vecteur est donc non nul tant que P est dans la bobine.
Par contre, je n'ai pas bien compris
Les variables de dérivation qui interviennent dans les opérateurs (gradient, divergence, laplacien, rotationnel) sont les coordonnées de M, le point où on étudie le champ.
Si un courant circule dans la bobine, le potentiel vecteur n'est pas nul au voisinage de la bobine et, à l'extérieur de la bobine, la densité de courant est nulle donc :
Relis très attentivement mon message précédent. Il contient quelques subtilités qui devraient t'aider à mieux comprendre le cours d'électromagnétisme ...
Merci,
Je pense avoir compris au final. Merci beaucoup
Pour le champ magnétique, est ce que vous avez un document ou une explication du champ tournant (p=2+) (car même avec le lien, je n'arrive pas à bien voir) ?
Pour finir, dans notre cas on va calculer le champ crée par les deux sources (aimant rotor + courant stator), le théorème de superposition est il valide ? (les potentiels A vont donc s'ajouter ?)
Merci!
le théorème de superposition est il valide ? (les potentiels A vont donc s'ajouter ?)
Oui bien sûr.
Pour le champ magnétique, est ce que vous avez un document ou une explication du champ tournant (p=2+) (car même avec le lien, je n'arrive pas à bien voir) ?
A ce sujet, le document que je t'ai fourni "règle" le problème en une phrase...
La justification habituellement fournie en électrotechnique est la suivante :
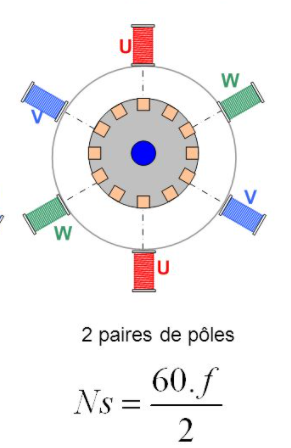
On commence par faire la démonstration faite dans le message précédent concernant un stator avec 3 bobines à 120°. On constate que, pendant une durée d'une période T du courant sinusoïdal, la direction du vecteur B passe de l'axe d'une bobine pour revenir à l'axe de la même bobine, celle alimentée par la même phase. Cela donne donc un tour par période du courant.
Imaginons maintenant 6 bobines à 60° de façon qu'une bobine du stator et la bobine diamétralement opposé soient reliées à la même phase (voir schéma sur document fourni). En une période du courant, pour passer de l'axe d'une bobine à l'axe de la bobine alimenté par la même phase, la direction de B tourne de seulement un demi tour. Sa vitesse de rotation est donc
/2.
Je suis conscient qu'il ne s'agit pas, comme souvent en électrotechnique, d'une véritable démonstration...
D'accord, merci
Donc ensuite le champ de l'aimant va suivre le champ tournant (avec 4 poles donc 2 aimants).
Je reste sur le sujet de l'electromag.
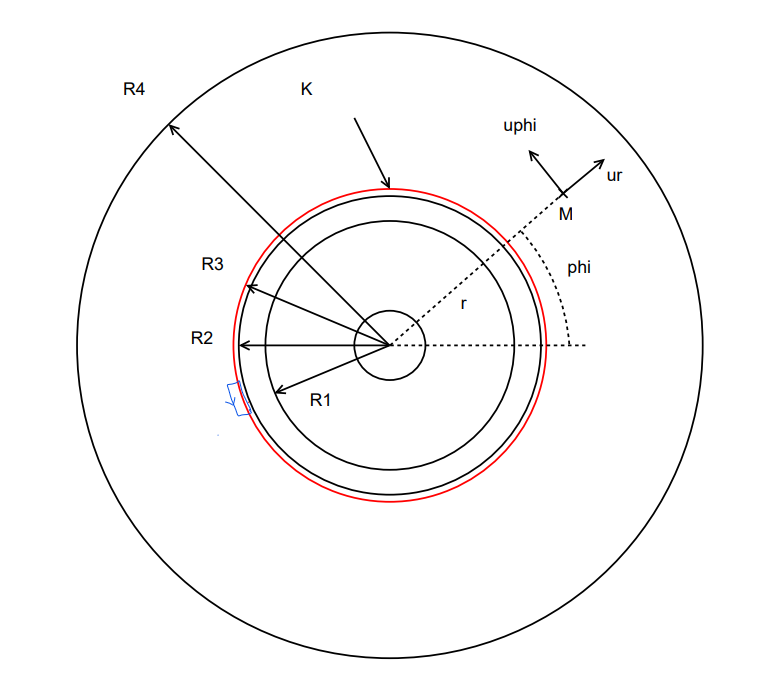
Lorsque l'on fait le théorème d'ampère, on prend sa composante H suivant pour utiliser la condition de passage entre 2 milieux. H dans notre cas n'a donc pas de norme connue, on peut donc le considérer dans le sens que l'on veut ?
ou
(voir dessin)
Le courant linéique étant K = Ks* cos(p phi)
On peut donc avoir (l1=l2 = l )
La longueur perpendiculaire au courant étant quasi nulle.
Merci !
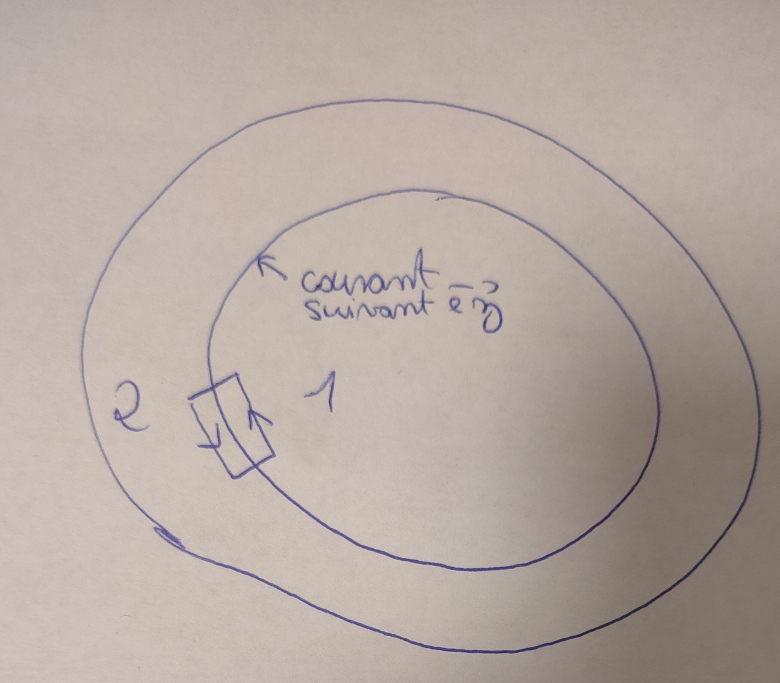
Pas sûr de bien comprendre le contexte. S'il s'agit d'étudier l'éventuelle discontinuité de la composante tangentielle du vecteur à la traversée de la surface, le sens de circulation peut être quelconque ; on obtient le même résultat...
Merci,
En fait je parle du vecteur H (son sens), pas du contours qui peut être choisi comme on veut.
Je m'explique surement mal...
Effectivement, la méthode fournit une relation de continuité ou de discontinuité sans renseigner sur le sens du vecteur. Il faut un renseignement supplémentaire qui dépend de la situation : sens de l'aimantation , sens du courant dans les bobines sources, nature des pôles d'un aimant, ... Rien dans ce que tu as écrit ne permet de répondre.
Dans notre cas, je n'ai pas plus d'information que cela, du coup je fais comment ? On ne peut pas le prendre dans un sens ?
Peut-être qu'avec un énoncé intégral et un schéma précis... Car là, à part rester dans les généralités comme je l'ai fait ???
En fait, il n'y a pas d'énoncer sur cela mais il faut se servir des conditions de passages (entre chaque milieu) pour trouver les coefficients lorsque l'on résoud
Par symétrie on a A suivant ez et qui dépend de r et phi.
En rouge, sur la photo c'est une densité de courant Ks = K cos(p phi). En bleu c'est l'interface entre l'entrefer et le stator.
Je sais pas si ça aide...
Annuler
connectez vous