Inscription / Connexion Nouveau Sujet
Moteur synchrone schéma
Bonjour,
Je viens à vous car sur internet j'ai vu qu'il existait 2 représentations pour un moteur synchrone.
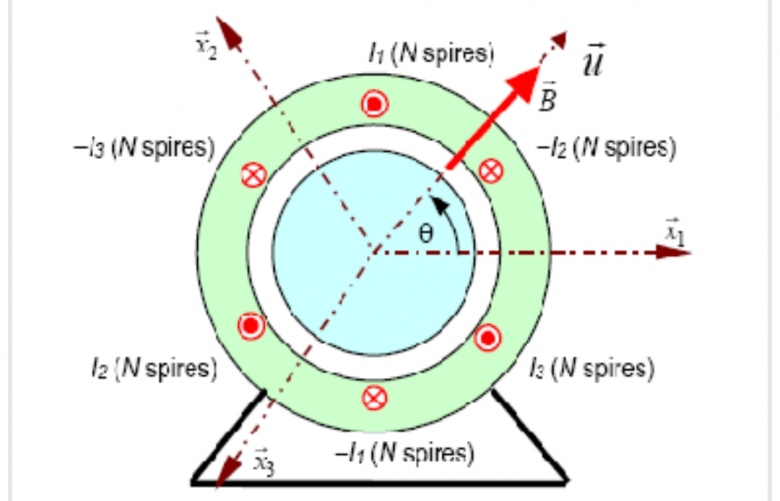
Je ne comprends pas la représentation avec les 6 "points", ils doivent sans doutes représenter les 3 bobines alimentées en courant...
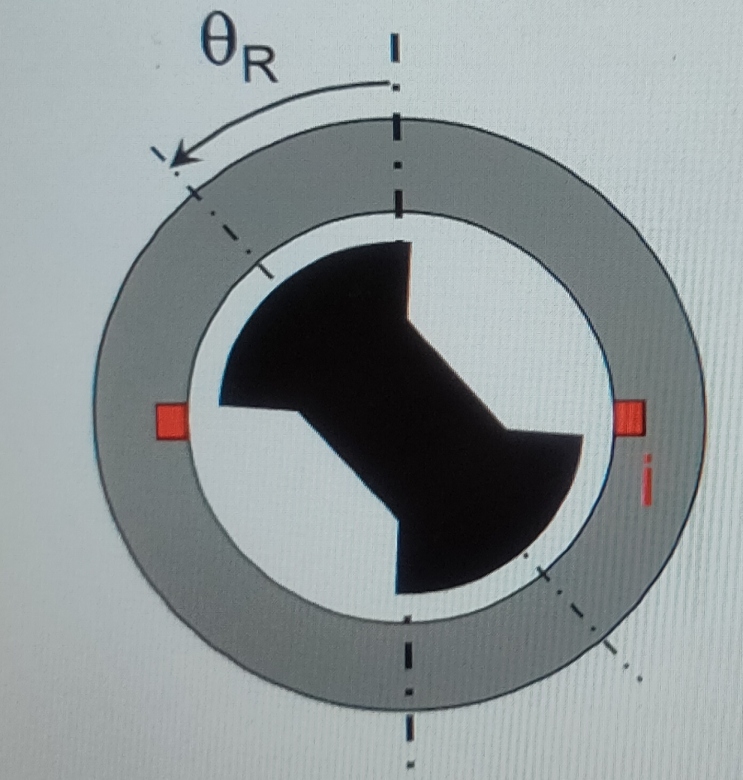
Et enfin sur le dernier schéma (avec tetha R), la bobine comment est t'elle en réalité ?
Merci !
Bonjour
Le schéma est une coupe du moteur par un plan perpendiculaire à l'axe de rotation du rotor. Le "rond" noté I1 correspond à la trace dans ce plan d'un côté de la bobine rectangulaire n°1 du stator, la "croix" notée -I1 correspond à la trace dans le plan du coté opposé de la bobine rectangulaire ; ainsi, si le coté supérieur de la bobine est parcouru par un courant circulant vers l'avant de la figure (sens symbolisé par un point), le côté inférieur est parcouru par un courant de même intensité mais orienté vers l'arrière de la figure (sens symbolisé par une croix).Selon la loi de Biot et Savart, cette bobine crée un champ magnétique de vecteur :
De même la bobine n° 2, d'axe x2 crée un champ magnétique proportionnel à i2. Je ne rappelle pas les propriétés des courants triphasés (pose des questions si tu le juges utile) :
De même, la bobine n° 3 d'axe x3 crée un champ magnétique proportionnel à i3 :
Je te laisse démontrer que le vecteur somme :
est un vecteur de norme constante, colinéaire au vecteur unitaire , ce vecteur tourant autour de l'axe du rotor à la vitesse angulaire
 .
.
N'hésite pas à poser des questions complémentaires si tu le juges utile.
Merci beaucoup,
Il ne manque pas un racine(2) pour le courant "I" et "k" est donc égal à ?
Les 3 bobines sont donc enroulées autour du rotor (voir schéma), il y a donc plusieurs disposition des bobines avec l'images des 3 bobines formants un triangle sur le stator ?
J'ai donc une expression de B : , si on prend la phase à l'origine du courant phi = 0, on peut s'implifier.
Si t=0 (angle =0), on a
car
Si t= T/3 (angle = 2pi/3), donc
J'ai un deuxième problème de compréhension, sur le schéma avec (tétha R). On parle de reluctance variable. La bobine est donc enrouler sur le stator aussi, B est donc vertical. Lorsque l'angle = 0, on a donc la reluctance qui est très élevée (au niveau de la bobine) car l'entrefer est très grand. Donc l'inductance qui est égal à N² / R est minimale. Lorsque l'angle = pi/2, la réluctance est petite car l'entrefer est petit donc l'inductance est maximale ? (car sur ma correction c'est l'inverse d'où l'incompréhension...).
Je sais que je vous en demande beaucoup, mais lorsqu'on alimente une bobine, elle créée du H (excitation mag), et donc comme elle n'a pas d'aimantation H = B (champs mag) ? Donc la création de H créée du B (hystérésis) ...
Merci infiniment !!
Je pense que tu as compris l'emplacement des bobines.
Il ne manque pas un racine(2) pour le courant "I"
J'ai noté Im l'intensité maximale que j'aurais aussi pu noter comme le produit de l'intensité efficace par
 2.
2.
et "k" est donc égal à
B est effectivement proportionnel à N mais l'expression de k n'est pas aussi simple. Elle dépend de la géométrie des bobines et aussi de la présence de fer, matériau ferromagnétique qui, pour une valeur de l'intensité du courant dans la bobine, permet d'obtenir un champ magnétique beaucoup plus intense que dans l'air.
Pour la suite : il faut revoir ton calcul ; il faut commencer par exprimer les vecteurs unitaires
 /3 et 4
/3 et 4 /3 caractéristiques des courants triphasés équilibrés.Revois si nécessaire ton cours sur le sujet.
/3 caractéristiques des courants triphasés équilibrés.Revois si nécessaire ton cours sur le sujet.Merci,
Du coup, oui j'ai pas tout pris en compte.
Pour le courant triphasé, je ne comprends pas pourquoi on a pas :
i1 = I cos(wt); i2=I cos(wt + 2pi/3) ; i3=I cos (wt -2pi/3) si on prend le sens trigo, comme les tensions, car le courant suit la tension. Ou alors c'est juste pour dire que quand wt = 2pi/3, B2 est max.
Donc
Je ne suis pas sur pour ici...
Si on prend phi = 0
Pas vraiment. Le but de la démonstration est d'obtenir : avec une norme du vecteur
constante. Je choisis un axe (Oy) dirigé par un vecteur unitaire
appartenant au plan de figure, vertical ascendant et ainsi orthogonal au vecteur unitaire
. Ainsi :
En trigonométrie : ; donc :
Ainsi :
Je te laisse exprimer la somme dans la base
puis montrer que
est un vecteur de norme constante, colinéaire au vecteur unitaire
, ce vecteur tournant autour de l'axe du rotor à la vitesse angulaire
 .
.
Tu m'as aussi posé une question sur la signification de l'angle  R sur le dernier schéma. La notion de vecteur moment magnétique d'une bobine ou d'un aimant permanent : cela te parle ?
R sur le dernier schéma. La notion de vecteur moment magnétique d'une bobine ou d'un aimant permanent : cela te parle ?
Cela donne dans la base x1 y1
On sait que
On voit par identification que wt+phi = theta et donc
Sur le moment magnétique je sais que le , le moment magnétique c'est ce qui est à l'origine de l'aimantation.
Merci,
Pour le courant triphasé, je ne comprends pas pourquoi on a pas :
i1 = I cos(wt); i2=I cos(wt + 2pi/3) ; i3=I cos (wt -2pi/3) si on prend le sens trigo, comme les tensions, car le courant suit la tension. Ou alors c'est juste pour dire que quand wt = 2pi/3, B2 est max.
Pour ici, est ce que vous pouvez m'expliquer car c'est une notion importante.
Merci
En fait, je pense avoir compris.
Le courant suit la tension mais comme arbitrairement on a un sens direct avec V1 en premier puis V2 et V3 donc V2 est forcément -2pi/3 et donc I2
D'accord avec tes résultats du 28-08-21 à 15:26. Les trois bobines créent bien un champ magnétique de norme constante tournant à une vitesse angulaire égale à la pulsation des tensions d'alimentation.
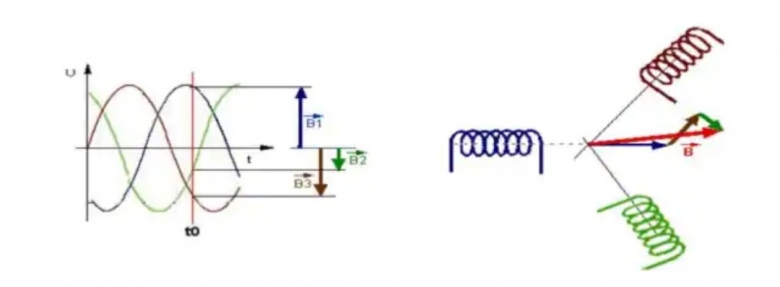
Les sinusoïdes tracées montre bien que u2 est en retard de phase de 2 /3 et que u3 est en retard de 2
/3 et que u3 est en retard de 2 /3 par rapport à u2 donc en retard de 4
/3 par rapport à u2 donc en retard de 4 /3 par rapport à u1. Bien sûr, comme les phases se mesurent modulo 2
/3 par rapport à u1. Bien sûr, comme les phases se mesurent modulo 2 , il est possible de considérer que u3 est en avance de 2
, il est possible de considérer que u3 est en avance de 2 /3 par rapport à u1 :
/3 par rapport à u1 :
Les caractéristiques des bobines du stator étant inconnues, il n'est pas possible de déterminer le déphasage entre la tension instantanée d'alimentation d'une bobine et l'intensité instantanée du courant qui la parcourt. Cependant, puisque les trois bobines sont identiques, ce déphasage est le même pour les trois bobines, d'où le " " que je fait intervenir dans les expressions des trois intensités instantanées.
" que je fait intervenir dans les expressions des trois intensités instantanées.
Le rotor est soit un aimant permanent soit une bobine parcourue par un courant continu. On peut le caractériser par un vecteur moment magnétique , d'où l'expression du couple moteur que tu as écrite, couple qui permet la rotation du rotor à la vitesse angulaire
 , d'où le nom : "moteur synchrone".
, d'où le nom : "moteur synchrone".
Je vous remercie pour ces explications !
Si j'en reviens à cela : mon raisonnement est donc faux et la correction est bonne (souvent c'est le cas  ) car B est vertical. Donc quand thetaR = 0 B est canalisé et l'entrefer est petit donc R petit et L grand. Pour thetaR = pi/2 c'est donc l'inverse car l'entrefer est grand.
) car B est vertical. Donc quand thetaR = 0 B est canalisé et l'entrefer est petit donc R petit et L grand. Pour thetaR = pi/2 c'est donc l'inverse car l'entrefer est grand.
Sur le schéma avec (tétha R). On parle de reluctance variable. Lorsque l'angle = 0, on a donc la reluctance qui est très élevée car l'entrefer est très grand. Donc l'inductance qui est égal à N² / R est minimale. Lorsque l'angle = pi/2, la réluctance est petite car l'entrefer est petit donc l'inductance est maximale ? (car sur ma correction c'est l'inverse d'où l'incompréhension...).
Je sais que j'ai beaucoup de questions
 , parfois je vois la tension en temporelle avec un cos
, parfois je vois la tension en temporelle avec un cos
E = cos (wt + phi)
Parfois avec un sin
E= sin (wt + phi)
Je me demande donc si il y a une sorte de convention car des fois un sinus permet de simplifier une expression.
Je ne comprends pas trop ton raisonnement sur l'entrefer... Il s'agit toujours d'un moteur synchrone triphasé ?
Pour ta deuxième question, il s'agit juste d'une questions de notations liée au choix de l'origine des dates : remplacer un sinus par un cosinus revient à décaler la phase de  /2 donc à décaler l'origine des temps d'un quart de période. Les calculs ne sont ni plus simples ni plus compliqués en utilisant le cosinus plutôt que le sinus. Disons simplement qu'utiliser un cosinus permet de considérer la grandeur physique associée comme la partie réelle de la grandeur complexe associée alors qu'utiliser un sinus conduirait à considérer la grandeur physique comme la partie imaginaire de la grandeur complexe associée. L'évolution des programmes de math a peut-être aussi influencé le choix plus fréquent du cosinus. Le cosinus est introduit plus tôt en math lors de l'étude des projections orthogonales puis des produits scalaires...
/2 donc à décaler l'origine des temps d'un quart de période. Les calculs ne sont ni plus simples ni plus compliqués en utilisant le cosinus plutôt que le sinus. Disons simplement qu'utiliser un cosinus permet de considérer la grandeur physique associée comme la partie réelle de la grandeur complexe associée alors qu'utiliser un sinus conduirait à considérer la grandeur physique comme la partie imaginaire de la grandeur complexe associée. L'évolution des programmes de math a peut-être aussi influencé le choix plus fréquent du cosinus. Le cosinus est introduit plus tôt en math lors de l'étude des projections orthogonales puis des produits scalaires...
Le schéma du paragraphe 5.1 correspond à quel dispositif exactement ? Que désigne exactement l (L minuscule) ?
Apparemment, l'auteur utilise la formule de l'énergie magnétique emmagasinée par autoinduction :
avec un couple de moment : puis considère l'intensité du courant fixe.



