Inscription / Connexion Nouveau Sujet
Le pendule qui bat la seconde
Bonjouur
J'ai besoin d'aide pour un exercice compliqué
Un pendule simple est constitué d'une bille de masse m , suspendu a un fil rigide de longueur l dont la masse est négligeable. Si l'on écarte le pendule de sa position de repos, il se met a osciller. Un aller et retour constiture une oscillation, et sa période est une période T qui peut se mesurer en seconde.
Afin de réaliser un pendule dont la période est d'une seconde un groupe d'élèves mesure 10 périodes, en faisant varier en premier la masse m de la bille, puis la longueur l du fil
Expérience une , pour l= 50 cm
m(g) 50 100 150 200
10 T(s) 14,1 14,1 14,0 14,2
Expérience deux , pour m= 100g
l(cm) 25 35 45 60
10 T(s) 10,1 12,0 13,5 15,5
1.a. Pourquoi mesurer 10 périodes et non une seule ?
b. Comment calculer la période pour chaque série de mesure ?
2. Que peut-on en déduire quand à l'influence de la masse sur la période du pendule.
3.La longueur du fil a-t-elle une influence sur la valeur de la période?
4. Pour une période d'une seconde, quel est l'ordre de grandeur de la longueur l à utiliser?
5. Pour vérifier si la période T est proportionnelle à la longueur l , tracer les deux courbes suivantes; T en fonction de l et T en fonction de l.
a.Quel est le graphique le plus simple à exploiter ?
b.En déduire une relation entre T et l ?
c.Le professeur qui encadre le groupe lui propose la relation suivante: T= 2 l/g avec g= 9,8 N.kg-1 ( intensité de pensanteur terrestre sur la Terre)
Verifier si la relation trouvée à la question 5.b est cohérente avec cette expression.
d. Calculer la longueur exacte de l pour que la période soit d'une seconde.
Je comprends vraiment rien.. merci d'avance
Salut,
Alors, Pour la Q1 c'est simplement pour une question de précision, en effet, si il y a des erreurs de mesures sur 10 T, alors il y en aura 10 fois moins pour 1 T (j'ai pas répondue à la Q1.b là ?? ^^)
Q2 : essaye de reformuler la question : est ce que la masse à une influence sur T ?? Pour avoir la réponse il suffit de regarder quand la masse varie et regarder sur T varie.
Q3 : cf Q2
Q4 : On a mesuré à chaque fois 10 T donc il faut dé&terminer 1 T et regarder la longueur l qui correspond (c'est un calcul très simple)
Q5 : Pour faire la comparaison avec les maths : T en fonction de l <=> T=f(l) (en maths c'est y=f(x)). T'as compris là ??
Après il n'y a plus de réflexion, c'est de l'exploitation de courbe bête et méchante
Bonne chance.
Le truc c'est que je suis nul en maths aussi alors la 5 pas trop compris. :S
Pour la 4) 10,1 divisé par 25 ? Pour en avoir qu'une seule?
Tu ne peux pas comprendre la question 5, tu l'as mal copiée.
Cela devrait sûrement être :
5)
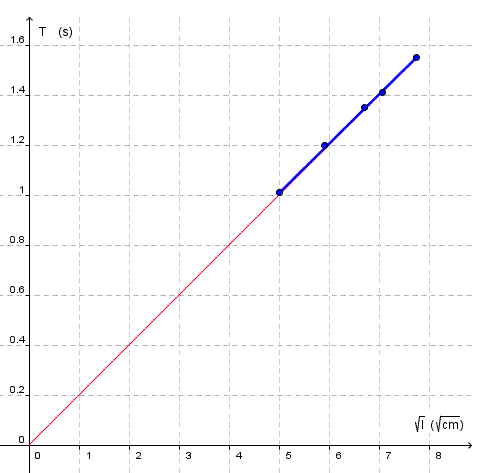
5. Pour vérifier si la période T est proportionnelle à la longueur l , tracer les deux courbes suivantes :
T en fonction de l et T en fonction de .
Pour tracer la courbe T en fonction de , tu calcules les
dans le tableau:
et on a alors :
Et tu traces T en fonction de à partir de là ...

Bonjour,
Une remarque :
Un pendule qui "bat la seconde" est un pendule dont la période vaut 2 secondes.
Un pendule simple qui bat la seconde a donc une longueur d'environ 1 mètre (et lors de la préparation du système métrique les physiciens avaient hésité à utiliser cette propriété pour définir l'unité de longueur).
Tu n'es pas le premier élève à poster cet exercice et l'erreur ne vient pas de toi mais de ton livre.

Et peux-tu donner quelques autres pistes sur ce devoir ? Je galère aussi sur le sujet, alors un peu d'aide serait la bienvenue ! Merci d'avance.
Oui pardon, bonjour.
J'ai déjà fait toutes les premières questions dont le graphique qui est proposé, cependant c'est pour la suite de l'exercice à partir de là : le petit b, c et d de la question 5.
Et merci de la rapidité de la réponse !
Question 5b
Au programme de l'année dernière, en troisième au collège, et revu cette année en seconde au lycée :
. fonctions affines et fonctions linéaires ; la forme de ces fonctions...


 dans son message du 11 mars à 11 h 34
dans son message du 11 mars à 11 h 34