Inscription / Connexion Nouveau Sujet
Le nombre d'atomes dans un cube
Bonjour, ça fait déjà plusieurs fois que j'essaie de resoudre cet exercice. Je pense que vous avez du le rencontrer plusieurs fois ce problème. Dans un cube de 2mm les atomes sont empilés régulièrement et se collent on me dit que le diametre de l'atome est de 0,25nm.
-je convertit le tout en metre puis je calcule le volume du cube (a×a×a) je trouve 8.10exp-9 m3 et 2,5.10exp-10m
-puis je calcule le volume de l'atome en partant du fait que si il a un diamètre dans l'espace l'atome est forcement une sphère.
Volumea= 4pi×Rexp3 donc je fait mon calcule puis je divise le volume du cube par celui de l'atome
J'aimerais avoir votre avis sur ma demarche parce que j'ai l'impression de m'être gouré quelque part merci pour votre attentio.
Bonjour,
La démarche est assez bonne. Mais en calculant ainsi tu imagines qu'il n'y aura plus aucun espace entre les atomes.
Or si tu empiles des sphères il reste de l'espace entre ces sphères.
Tu as déjà vu sur un marché les oranges empilées. Il y a des espaces entres les "sphères".
Le calcul exact est un peu compliqué pour un élève de seconde. Mais tu peux avoir une meilleure approximation (qui sera encore une approximation) en supposant que chaque atome est un cube de 0,25 nm de côté
Cette nouvelle approximation te permettra, avec ce que tu as déjà fait, d'avoir un encadrement de la valeur réelle.
Salut,
Ton impression est bonne, c'est effectivement faux.
Ta méthode marcherait si les atomes étaient des petits parallépipèdes et qu'il n'y avait pas de vide entre les atomes.
Prend une sorte de balle:
des ballons de basket
de foot
balle de tennis
de pingpong.
...
Choisit un des sorte de sphère et mets les dans une boite carré, tu vas perdre plein de place, il se passe la même chose pour les atomes.
tu peux voir une image en ciiquant sur
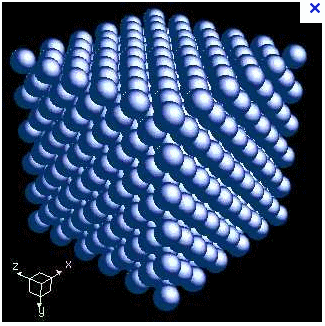
Edit Coll : image placée sur le serveur de l' 
; elle est "trop" belle ; bonjour lamat !
Un ami a moi m'as dit que je pouvais calculer le nombre d'atome sur une arête puis mettre le tout au cube pensez vous que cette methode Est envisageable sachabt que je dois obligatoirement convertir je ferrais donc (2.10exp-3m × 2,5.10exp-9m)exp3 ?
Je reprends donc la main...
Volume du cube de 2 mm de côté : Vcube = (2.10-3)3 = 8.10-9 m3
Volume d'un atome, sphère de 0,25 nm de diamètre Vatome = (4/3).
.(0,125.10-9)3 
8,18.10-30 m3
Première méthode
On suppose que les sphères remplissent le cube sans laisser aucun espace :
Nombre d'atomes : Vcube / Vatome 8.10-9 / 8,18.10-30 9,78.1020 atomes
On sait qu'il n'est pas possible pour des sphères d'être rangées dans un cube sans laisser d'espace vide. Donc on peut en conclure que ce nombre est trop élevé.
Deuxième méthode
On place chaque sphère dans un petit cube de 0,25 nm de côté et on range ces petits cubes dans le grand cube.
Cette méthode est la même que celle que te proposait ton ami : combien d'atomes sur une arête du cube et élévation au cube.
Volume d'un petit cube de 0,25 nm de côté : Vpetit = (0,25.10-9)3 = 1,562 5.10-29 m3
Nombre de petits cubes que l'on peut ranger dans le grand cube : Vcube / Vpetit = 8.10-9 / 1,5625.10-29 5,12.1020
À peu près deux fois moins qu'avec la première méthode, ce qui se comprend facilement :
Une sphère de rayon R se place dans un cube de côté 2R
Le volume du cube est à peu près deux fois celui de la sphère : (2R)3 / [(4/3)..R3] = 8 
3 / (4 ) = 6 / 1,9
Avec cette deuxième méthode on a un nombre trop petit.
C'est pour cela que j'avais écrit (29 à 10 h 56) que l'on obtiendrait un encadrement.
Troisième méthode
On trouve dans le forum de mathématiques le calcul du remplissage selon une maille cubique à faces centrées, c'est-à-dire le remplissage des oranges au marché, ou le remplissage de la très belle image postée par lamat
Tous calculs faits, le rapport du volume occupé par le volume total vaut
On trouve alors ici que le volume occupé vaut Vcube [(
2)/6] 5,92.10-9 m3
Le nombre d'atomes correspondants est donc 5,92.10-9 m3 / Vatome 5,92.10-9 / 8,18.10-30 7,24.1020 atomes
____________
Voilà.
Deux méthodes faciles qui donnent un encadrement du résultat : entre 5,12.1020 atomes et 9,78.1020 atomes
Une méthode qui est un peu plus difficile, mais vite accessible dès que l'on a fait un peu de géométrie dans l'espace et qui donne la vraie valeur : 7,24.1020 atomes
Les ordres de grandeur donnés par les trois méthodes sont les mêmes !
Je sens que vais prendre du temps a tout assimilé et a comprendre mais je vais m'y mettre sérieusement merci pour ce coum de main de génie (y)
Les calculs de géométrie dans l'espace (ou de cristallographie...) montrent que :
Voccupé / Vcube 0,74 (très exactement )
Donc le volume qui est celui des atomes présents dans le cube vaut :
Voccupé = Vcube
Annuler
connectez vous