Bonjour.

Je ne sais pas trop comment on traite ce genre de problème actuellement, il y a quelques années on utilisait une relation barycentrique du type :
Est-ce que cela vous parle ?

A vous.

Merci d'abord picar pour la relation barycentrique je sais mais dit moi le G1 et G2 vont représente quelle mesure??

G₁ est le centre d'inertie de la roue déséquilibrée, G₂, celui de la surcharge dont il faut déterminer la masse m₂.

Ok donc nous allons faire une équation pour tirer M2 nespa??? Mais il ya une deuxième inconnue G2  voilà mon problème

Bonjour, Parkryc Svp est ce que vous pouvez me donnez ta résulte que vous avez trouvé . et Merci.

Je ne vois pas ce qui vous arrête.

Les positions de G₁ (centre d'inertie de la roue déséquilibrée),  G₂ (centre de d'inertie de masselotte) et G (centre d'inertie de la roue équilibrée) sont connues, la valeur de la masse m₁ est également connue.

Faites un schéma sur lequel vous placerez G₁,  G₂ et G, puis, transformez la relation barycentrique en relation numérique et enfin, sortez la valeur de m₂.

oui je sais, mais je ne sais est ce que ma résulte est juste j'ai trouvé:  -1/m2=OG

A Salma.
Détaillez un peu votre calcul, car il y a manifestement une erreur de signe.
Et puis, qu'appelez vous O ?

Ceci mis à part, il me semble que vous êtes sur la bonne voie.

Oui, c'est vrai dsl
donc O (l'axe de rotation ) et la résulte ext -1/m2=OG2 ( avec vecteur) ,et G2 (centre de masselotte)

A Salma.
Ce qui ne va pas, c'est que vous traitez les vecteurs et les nombres de la même manière.

On a bien :

          

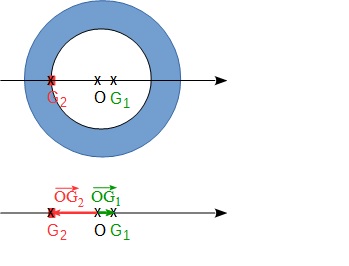
Si vous regardez le schéma, vous constatez que et sont de sens contraire. L'un () est dans le sens positif de l'axe , l'autre () en sens inverse de l'axe.

Quand on passe aux valeurs, il faut tenir compte de cette position particulière des deux vecteurs.

On compte alors positivement la norme de et négativement celle de .

On écrit alors :

Numériquement, cela donne :     (les longueurs étant exprimées en cm et les masses en kg).

En effectuant, on obtient :     soit :  

Finalement on trouve

OK ?

oui c'est juste,  mais le problème que j'ai rencontré c'est la position de G2 et par suite ma méthode soit juste
merci beaucoup
car j'ai une examen de physique sur ce sujet

Alors bon courage pour l'examen et à une prochaine fois peut-être.