Inscription / Connexion Nouveau Sujet
La terre autour du soleil
Bonjour à tous,
Dans mon devoir de physique (je fais l'école par correspondance), il y a un exercice que je ne comprends absolument pas:
EXERCICE 4:
La Terre autour du soleil
on utilise l'image qui est en pièce jointe.
Pour simplifier l'exercice, nous considérons que l'axe de rotation de la Terre (rotation sur elle-même) et l'axe de rotation de la Terre (rotation autour du Soleil) sont parallèles.
1) Un homme est immobile sur l'équateur. Quelle est sa trajectoire dans un référentiel Rt(O; i, j) sur le i et le j il y a une flèche mais je ne sais pas comment le faire....
avec O centre de la Terre. Faire un dessin. ==> Alors, là je n'y comprends rien du tout! Si, vous pouviez m'éclairer et m'aider à comprendre, je vous en serai très reconnaissante.
Il y a d'autres questions, mais déjà je poste la première question pour comprendre, si je comprends la 1ère, je comprendrai les autres...
Merci d'avance,
Bien cordialement, bonne journée à tous!
Andréa 
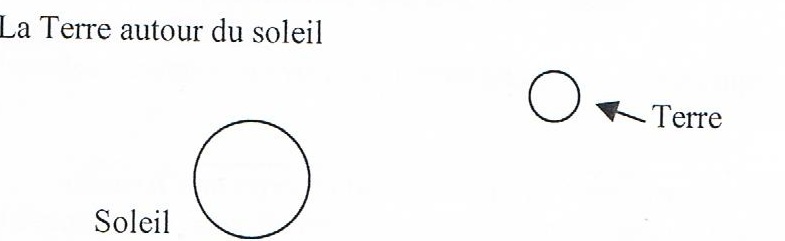
Bonjour,
O est le centre de la Terre : facile à dessiner.
On peut supposer que les axes de rotation (parallèles ! donc il n'y a plus de saisons, les jours et les nuits durent toujours 12 heures, et cela en tous les points de la Terre... mais ce n'est pas le sujet) sont tous deux perpendiculaires au plan de la figure.
Le repère (0 ;  ,
,  ) associé au référentiel n'est pas suffisamment défini, et donc le référentiel n'est pas défini non plus.
) associé au référentiel n'est pas suffisamment défini, et donc le référentiel n'est pas défini non plus.
Le référentiel est-il terrestre ? Auquel cas les vecteurs  et
et  vont tourner en même temps que la Terre dans son mouvement de rotation autour d'elle-même.
vont tourner en même temps que la Terre dans son mouvement de rotation autour d'elle-même.
Le référentiel est-il géocentrique ? Auquel cas les vecteurs  et
et  resteront parallèles à eux-mêmes alors que la Terre tournera sur elle-même.
resteront parallèles à eux-mêmes alors que la Terre tournera sur elle-même.
La trajectoire d'un homme immobile sur l'équateur ne sera pas décrite de la même manière dans les deux cas.
En cliquant sur le bouton  qui se trouve sous le cadre d'écriture, tu trouveras de quoi bien écrire les vecteurs
qui se trouve sous le cadre d'écriture, tu trouveras de quoi bien écrire les vecteurs  et
et 

ok, d'accord, merci coll, pour vos explications claires et précises!
A bientôt!
Cordialement,
Andréa
Bonsoir,
Je sais que cela fait un moment que les messages ont été écrit mais j'ai le même exercice et même avec vos explications, je n'ai toujours pas compris.
Pouvez-vous m'aider ?  SVP (j'ai des difficultés en physique
SVP (j'ai des difficultés en physique  )
)
Merci d'avance.
Cordialement, Céline.
Bonjour Celinecd
Ce que j'ai écrit il y a près de trois ans, reste vrai...
Le référentiel n'est pas suffisamment défini par ce qu'a posté andreaaaa2
Le référentiel RT (O ;  ,
,  ) est-il terrestre ou géocentrique ?
) est-il terrestre ou géocentrique ?
Peux-tu poster l'énoncé complet sans y changer un seul mot ?

Bonjour,
l'énoncé complet est :
La Terre autour du soleil
on utilise l'image qui est en pièce jointe.
Pour simplifier l'exercice, nous considérons que l'axe de rotation de la Terre (rotation sur elle-même) et l'axe de rotation de la Terre (rotation autour du Soleil) sont parallèles.
1) Un homme est immobile sur l'équateur. Quelle est sa trajectoire dans un référentiel Rt(O;  ;
; ) sur le i et le j il y a une flèche mais je ne sais pas comment le faire....
) sur le i et le j il y a une flèche mais je ne sais pas comment le faire....
avec O centre de la Terre. Faire un dessin.
2) Quelle est sa trajectoire dans un référentiel lié au soleil Rs ? Faire un dessin
3) La terre tourne autour d'elle-même en 24 h. Le rayon de la Terre est 6375 km.
Quelle est la vitesse de l'homme (en m s^-1) dans Rt (question 1 ) ?
4) Quelle est la trajectoire du centre de la Terre dans Rs ?
5) La distance entre le centre du Soleil et celui de la Terre est de 149,6.10^6 km. Quelle est la vitesse du centre de la Terre dans Rs , en km.s^-1 et en m.s^-1 ?
Merci d'avance pour votre aide.
À la lecture de l'énoncé complet on va admettre (mais il aurait été préférable que l'énoncé soit bien rédigé...) que le référentiel RT : (O ;  ,
,  ) est un référentiel géocentrique.
) est un référentiel géocentrique.
Il est alors facile de répondre au moins à la première question...

Le référentiel RT : (O ;  ,
, ) est un référentiel géocentrique. Les vecteurs
) est un référentiel géocentrique. Les vecteurs  et
et  resteront parallèles à eux-mêmes alors que la Terre tournera sur elle-même.
resteront parallèles à eux-mêmes alors que la Terre tournera sur elle-même.
Sa trajectoire est circulaire.
1)
Dans un référentiel terrestre, il serait immobile
Dans un référentiel géocentrique, sa trajectoire est un cercle
2)
Dans un référentiel héliocentrique, sa trajectoire (surtout après la première question...) est très compliquée.
Elle est approximativement circulaire
À la question 4, tu diras quelle est la trajectoire du centre de la Terre autour du Soleil : c'est une trajectoire déjà un peu plus simple : un cercle en première approximation, une ellipse en seconde approximation (et quelque chose de très compliqué encore si l'on veut une très grande précision, en particulier, mais pas seulement, à cause de la présence de la Lune...)
Donc, l'homme immobile à l'équateur, décrit autour du Soleil, une courbe, proche d'un cercle mais légèrement "festonnée" à cause de la rotation de la Terre sur elle-même.
À toi pour les questions suivantes !

Merci Coll pour ton aide,
Je vais travailler la suite ce weekend, je posterai mes réponses lundi.
Bon weekend, 
Bonjour, 
Voici mes réponses :
3) V = d/t
Vh = d/t = (2π 6375.10^3) / (243600) = 463 m/s.
4) La trajectoire du centre de la Terre autour du Soleil est un cercle en première approximation, une ellipse en seconde approximation.
5) Vrs = d/t = (2π 149,6.10^9) / (365*24*3600) = 30 000 m/s
= 30 km/s
Est-ce bon ? 
Merci d'avance 
C'est bon.
Pour la réponse à la troisième question, tu as oublié un signe  au dénominateur : 24
au dénominateur : 24  3 600
3 600
À la question 5 tu as arrondi un peu "violemment". Pour ma part, j'annoncerais plutôt  29 800 m.s-1 ou
29 800 m.s-1 ou  29,8 km.s-1
29,8 km.s-1
__________
Pour aiguiser ta curiosité :
. dans le référentiel géocentrique la durée d'une révolution de la Terre sur elle-même est un peu plus courte que 24 heures. Plutôt 23 h 56 min 4 s ("jour sidéral"). La vitesse d'un point de l'équateur serait alors plutôt d'environ 465 m.s-1
. Là encore la durée d'une année n'est pas exactement 365 jours. L'année sidérale vaut environ 365,2564 jours solaires
. Et comme la trajectoire n'est pas un cercle mais une ellipse, cette vitesse varie continuellement ; plus rapide quand la Terre est proche du Soleil (par exemple en janvier pour nous dans l'hémisphère nord) et plus lentement quand la Terre est plus éloignée du Soleil (en juillet pour nous).