Inscription / Connexion Nouveau Sujet
la loi de Descartes
J'ai un exo j'ai essayé mais j'ai quelques problèmes:
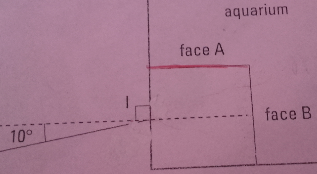
Un cube de verre est posé au fond d'un aquarium vide, contre la paroi. Un rayon lumineux arrive sur cette paroi de l'aquarium sous un angle d'incidence de 10degrés.
1) on envisage le cas ou le point d'entrée de la lumière dans le cube est tel que le rayon rétracté sort par la face B. Justifier sans calcul la valeur de l'angle sous lequel le rayon sort du cube. [J'ai trouvé 11,5degrés ]
De quel angle le rayon a-t'il été dévié par la passage à travers le cube de verre l'angle d'incidence]
2 ) on considère maintenant le cas ou le rayon sort par la face A. Quelle est la valeur de l'angle sous lequel il sort.
3)avec l'aquarium rempli quel est l'angle de déviation de la lumière au sortir du cube dans chacun des cas évoqués aux questions précédentes.
1)
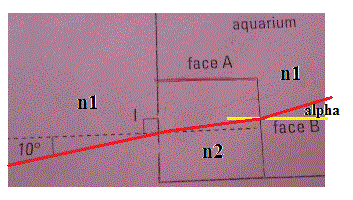
Soit r l'angle de réfraction du rayon sur l'interface air-verre
n1.sin(10°) = n2.sin(r)
Le rayon arrive sur la face B avec un angle d'incidence r (faire un dessin plus grand et montrer par les angles alterne-interne ce que je viens d'annoncer)
Soit alpha l'angle de sortie du rayon par rapport à la normale à la face B
n2.sin(r) = n1.sin(alpha)
En combinant les 2 relations trouvées ci-dessus, on a donc : n1.sin(10°) = n1.sin(alpha)
Et donc alpha = 10°
-----
2)
Si tu as compris la réponse à la question 1 ... tu devrais arriver à répondre à la question 2.
-----
...
Sauf distraction. 
Ben oui que j'ai une idée, mais c'est plutôt toi qui doit l'avoir.
Le problème 3 ressemble aux autres, avec la seule différence que lorsque le rayon arrive au niveau de la face B (ou de la face A), il va "sortir" vers un milieu dont l'indice de réfraction n'est pas le n1 que j'ai mis sur le dessin (à droite du dessin).
Pour les 2 premiers exercices, n1 = 1 (celui de l'air)
Pour l'exercice 3, quand le rayon arrive sur la face B (ou la face A), il va vers de l'eau dont l'indice de réfraction est environ 1,33.
Il faut donc tenir compte de cette valeur (1,33) de l'indice de réfraction de l'eau pour calculer la déviation du rayon au sortir du cube.

ok pour ces réponse mais comment fait on pour trouver l'angle de réfraction pour que le rayon sorte sur la face A ?
2)
Il suffit le déplacer le rayon d'entrée (parallèlement à sa direction initiale) pour que, après son passage dans le cube en verre, il rencontre la face A et plus la face B.
n1.sin(10°) = n2.sin(r)
sin(r) = n1/n2 * sin(10°)
cos²(r) + sin²(r) = 1
cos(r) = Racinecarrée[1 - (n1/n2 * sin(10°))²] (puisque r est un angle aigu)
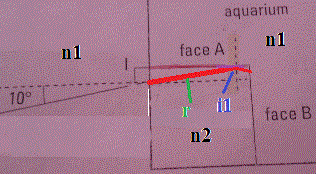
i1 = 90°-r
Au niveau de la face A :
n2.sin(i1) = n1.sin(r') (avec r' l'angle de réfraction niveau face A ... si il existe)
n2.sin(90°-r) = n1.sin(r')
n2.cos(r) = n1.sin(r')
n2 * Racinecarrée[1 - (n1/n2 * sin(10°))²] = n1 * sin(r')
sin(r') = (n2/n1) * Racinecarrée[1 - (n1/n2 * sin(10°))²]
Avec n1 = 1 (air)
et n2 = 1,5 environ (verre), on a donc :
sin(r') = (1,5/1) * Racinecarrée[1 - (1/1,5 * sin(10°))²]
et on trouve sin(r') > 1 ... ce qui est impossible.
Et donc, il y a réflexion totale au niveau de la face A , le rayon ne sortira pas par la face A.
Le rayon, va donc se réfléchir sur la face A ... et atteindra quand même la face B où il pourra sortir du cube.
Sauf distraction.