Bonjour,

En optique géométrique il faut obligatoirement utiliser les mesures algébriques des segments.

Formule de conjugaison pour une lentille mince de centre O, formule dite de Descartes
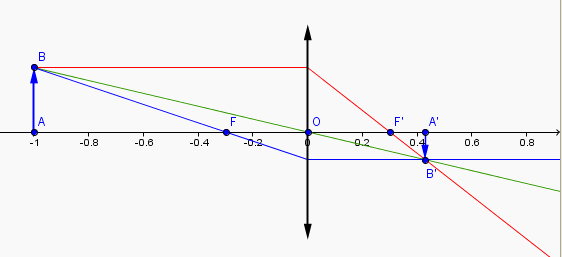
Le pied de l'objet est en A
Le pied de l'image est en A'
Le foyer image est en F'
L'axe optique est orienté (dans le sens de propagation de la lumière)



Que valent ici :

et

Donc mes calculs sont bon .

Mais j'avais un souci de construction que j'ai résolue entre temps .

Merci

Ton calcul est faux.

Je ne sais pas comment tu as pu faire la construction si tu as un tout petit peu cherché à respecter les distances (car le dessin ne peut vraiment pas correspondre à ce calcul qui est tout à fait faux).

Of'=0,3m ou 30 cm
OA=1m ou 100cm
soit 1/OA'-1/1=1/0,3 je suis restée en métre
donc équivaut à 1/OA'=1/0,3+1/1=4,33m


Donc si c'est faux explique moi ce qui l'est ?

Merci

Oui, c'est faux parce que tu n'as pas employé les mesures algébriques.

Que valent ici :

et

Bonjour

J'ai verifié mes cours il ne parle pas de valeur algébrique que veux tu dire par là?
Peux-tu m'expliquer?

Merci

Comme je te l'ai écrit :

L'axe optique est orienté dans le sens de propagation de la lumière. Donc de A vers O et de O vers A'

Généralement le centre optique de la lentille (le point O) est pris pour origine sur cet axe.

Donc je repose mes questions :

Que valent ici :

et

Of'=0,3m
OA=1m

D'accord pour

Mais pas d'accord pour

De O vers A on se déplace en sens inverse de celui de la propagation de la lumière...

OA=-1
donc je reprend la formule
1/OA'-1/-1=1/0,3
Soit 1/OA'=1/0,3+1/-1
1/OA'=1/1,3+1,3/-1,3
1/OA'=2,3/-1,3

Écriture très difficile à lire

Peux-tu me donner le résultat ?

environ 1, 76

je ne sais pas mettre mes calculs comme toi .

1,76 quoi ?

Plusieurs méthodes pour bien écrire une formule sur le forum :

Comment bien écrire une formule sur le forum ?

Tu n'es pas obligé(e) d'employer le
______________

Je reprends :

Formule de conjugaison pour une lentille mince de centre O, formule dite de Descartes
Le pied de l'objet est en A
Le pied de l'image est en A'
Le foyer image est en F'
L'axe optique est orienté (dans le sens de propagation de la lumière)



Or ici :

et


et donc


______________

Je ne sais pas si tu as fait une figure. Mais avec une figure bien faite on a une excellente idée du résultat. (ma figure attend ton résultat depuis avant-hier ! ).

Les valeurs que tu annonces sont impossibles à justifier avec une construction correcte de l'image donnée par la lentille.

Bonjour,

Désolée mais internet chez moi fonctionne très très mal.

Je reprends si ça ne coupe pas .

OA'=0,56m

Je prends comme echelle 1cm = 1 m
Est-ce judicieux ?

Merci de ton aide , meme si je suis longue à la détente, je prépare des cours par correspondance et des enfants à m'occuper et je peux te dire que c'est loin d'etre de la tarte mais je persiste , et je m'accroche.
.
Cordialement

Je cherche à t'aider et cela ne me dérange pas que tu prennes ton temps.

Mais je ne comprends vraiment pas comment tu peux trouver 0,56 m

Il s'agit de faire la soustraction de deux fractions...



et donc



Je te laisse faire cette division et choisir la bonne unité...

La on trouve pour OA'= 0,43

J'ai mélangé les additions et les multiplications j'ai fait 1+0,3 au lieu de 1X0,3 ce qui ne donne pas le meme resultat .

Merci encore de ton aide et de ta patience .

Cordialement
Passe un bon réveillon de noel .

j'ai oublié l'unité c'est en metre

Oui, environ 0,43 m

En cadeau de Noël, la figure :



Joyeuses fêtes !

Merci beaucoup pour ton aide .

Joyeux noel .

Je t'en prie. Joyeux Noël à toi aussi.
À une prochaine fois !

Re bonjour,

Peux-tu me confirmer mon calcul STP

On place une lentille divergente L2 de distance F'=-10
à une distance de L1 telle que O1O2=30 cm
Apres calcul O2 est -il bien egale à 70 cm
Soit OA=-70 cm ou -0,7 m
ce qui donne 1/OA'=1/-0,1+1/-0,7
OA'=0,11 m

zut  merci encore

Je suis désolé, mais je ne comprends rien à ce que tu fais.

Est-ce un nouvel exercice ?

Est-ce la suite de ce que tu as posté plus haut ? Alors pourquoi n'as-tu pas posté un énoncé complet ?

Si c'est la suite, je te demande de poster un énoncé complet et sans en changer un seul mot.
_____________

Si O₂ est un point alors un point ne peut pas être égal à 70 cm

Si et si

alors



Mais je ne vois pas du tout à quoi cela peut servir ! L'image donnée par une deuxième lentille n'est pas l'image de l'objet mais est l'image de l'image donnée par la première lentille...

Oui excuse moi je ne savais pas pour l'énoncé entier.
Cela fait partit de la suite de l'exercice et à priori je me suis trompée encore une fois .

Bonsoir,

Je te donne la suite de l'exercice.

On place une lentille divergente L2 de distance focale F'=-10 à une distance de L1 telle que O1O2=30 cm

Que représente l'image donnée par L1 pour L2 ? Calculer la position de l'image finale donnée par L2. Faire une construction.
effectivement comme ceci c'est plus comprehensible

Merci pour ton aide.

Cordialement

Je trouve OA'=-0,10 environ confondu avec F' elles est bizard cette figure !!!
Quelque chose me pertube !

Je recommence .

Puisqu'on ajoute une deuxième lentille, il va falloir être très rigoureux pour les notations, sinon ce sera incompréhensible.

Lentille convergente L₁
Centre optique : O₁ d'abscisse sur l'axe optique : 0
Foyer image : F '₁ d'abscisse +0,30 m
Foyer objet : F₁ d'abscisse -0,30 m

Cette lentille donne de l'objet AB une image A₁B₁ (je change les notations et remplace A'B' par A₁B₁)
A : abscisse -1,0 m
le début de l'exercice a permis d'établir que
A₁ a pour abscisse 30/70 m 0,429 m
___________

On ajoute la lentille divergente L₂
Centre optique O₂ : abscisse 0,30 m
On peut donc constater que le point O₂ est confondu avec le foyer image F '₁ de la première lentille (et cela sera très utile pour la construction de l'image donnée par l'ensemble ! )
Foyer image F '₂ : abscisse 0,20 m (attention, c'est une lentille divergente ! )
Foyer objet F₂ : abscisse 0,40 m
____________

Que réponds-tu à la question :
 

Bonjour coll.
Encore merci de ton aide et de tes explications .
Mais je m'embrouille un peu , tu me dis :

On ajoute la lentille divergente L2
Centre optique O2 : abscisse 0,30 m
On peut donc constater que le point O2 est confondu avec le foyer image F '1 de la première lentille (et cela sera très utile pour la construction de l'image donnée par l'ensemble ! )
Foyer image F '2 : abscisse 0,20 m (attention, c'est une lentille divergente ! )
Foyer objet F2 : abscisse 0,40 m

Pourquoi le centre optique O2 abscisse 0,3m , foyer image à 0,20m et foyer Objet 0,40 m.
Le foyer image ce n'est pas -O,1m et objet 0,10m. Tu me dis attention c'est une lentille divergente .

Peux-tu m'expliquer le pourquoi d'une telle différence pour commencer par là ?

Merci .

Parce que je ne change pas l'origine sur l'axe.

Je conserve comme origine de l'axe le centre optique O₁ qui nous a servi pour la première lentille.

Ce n'est pas gênant.

Le foyer image F '₂ de la deuxième lentille se trouve bien, comme tu l'écris, à 0,10 m avant le centre optique O₂ de la lentille L₂ (puisque c'est une lentille divergente)

Puisque

et que l'abscisse du point O₂ est + 0,30 m

on trouve bien que l'abscisse du point F '₂ vaut + 0,30 - 0,10 = 0,20 m
etc.

Ce qui compte ce sont les mesures algébriques des segments.
Les abscisses sont pratiques par exemple pour faire la figure.

Il faut répondre à la question :
 

L'image de L1 représente l'image de L2.

Donc je reprend mes calcul car mon cerveau est lent !!!
1/OA'=-1/0,2-1/1,3
1/OA'=-1,5/0,26
OA'=-0,17 m

Je fais mon schéma avec ceci pour verifier que j'ai bien pigé .

Merci

L'image donnée par la lentille L₁ devient l'objet pour la lentille L₂

Avant de te lancer dans les calculs (qui sont faux) il faut répondre aux questions suivantes :
Notant O₂ le centre optique de la lentille divergente L₂

Que vaut ?

Que vaut ?

Je te rappelle que je nomme A₁ le pied de l'image donnée de A par la lentille L₁ ; l'abscisse de ce point A₁ vaut 30/70 m

Avec ces bonnes valeurs, tu pourras calculer et ainsi la position de l'image donnée de A par l'ensemble des deux lentilles.

Je ne pourrai plus te répondre avant vendredi dans l'après-midi.

Je te donne la figure et la position de l'image finale :



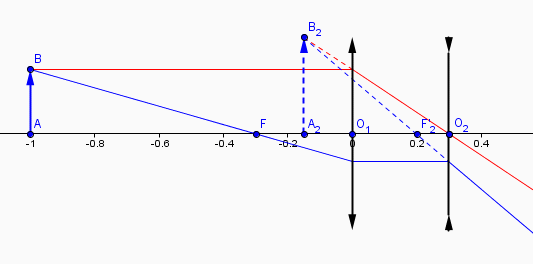
Tu dois (si tu ne te trompes pas dans les signes ! ) trouver que
et, en conséquence,
l'abscisse du point A₂ est de -0,15 m

Selon l'expression consacrée par J-P : "Recopier sans comprendre est inutile"

En fait coll j'étais partie sur ceci :
e suis désolé, mais je ne comprends rien à ce que tu fais.

Est-ce un nouvel exercice ?

Est-ce la suite de ce que tu as posté plus haut ? Alors pourquoi n'as-tu pas posté un énoncé complet ?

Si c'est la suite, je te demande de poster un énoncé complet et sans en changer un seul mot.
_____________

Si O2 est un point alors un point ne peut pas être égal à 70 cm

Si  et si

alors



Mais je ne vois pas du tout à quoi cela peut servir ! L'image donnée par une deuxième lentille n'est pas l'image de l'objet mais est l'image de l'image donnée par la première lentille...


Ensuite j'ai inscrit le reste de l'enoncé au complet.
En fait par ma faute cela m'a perturbé dans l'exercice .
J'ai fait la construction et elle est bien différente!! Ce que je ne comprends pas, c'est que la deuxième lentille est divergente alors que la première et convergente .Dis moi pourquoi F'1 et F'2 sont positif alors que pour la lentille divergente F'2=-10cm.
Je ne sais pas si je suis claire , j'ai besoin de bien comprendre et je peux attendre Vendredi.
Merci pour tes explications je vais chercher sur internet pour comprendre encore mieux cet exercice .

Encore merci.

Cordialement.

Il est impossible de faire un exercice sans avoir appris le cours correspondant.

Tu ne savais pas qu'il faut obligatoirement employer les mesures algébriques des segments.
Tu dis ne pas connaître la différence entre une lentille convergente et une lentille divergente.

N'as-tu pas de cours ?

Bonjour coll,

si j'ai des cours mais ils sont sommaires .
Je suis obligée de compléter avec d'autres livres ou chercher des explications sur le net .

Si tu veux pour moi dans l'ennoncé F' est à -10 cm .
Donc je l'ai positioné à -10cm ou -0,1m, et la lentille a -130 cm ou 1,3m.
Les calculs que tu as fait ne me sont pas expliqués dans mes cours .
Imagine la difficulté si je n'ai pas tout.
Si tu as un cours la dessus je suis preneuse .

Merci en tout cas .

Cordialement

Ce qu'il faut absolument savoir :
. l'axe optique est orienté ; généralement dans le sens de propagation de la lumière depuis l'objet ; souvent les schémas sont faits avec l'objet à gauche et donc l'axe optique orienté de la gauche vers la droite (c'est le cas de mes deux dessins ci-dessus)
. sur l'axe optique une origine des abscisses est définie ; ici j'ai choisi le centre optique O₁ de la première lentille
. il faut obligatoirement utiliser les mesures algébriques des segments : donc, la longeur du segment avec le signe + si de l'origine vers l'extrémité on se déplace dans le sens positif de l'axe optique et le signe - sinon.
. la distance focale d'une lentille convergente est positive ; ici
. une lentille convergente qui reçoit des rayons parallélement à l'axe optique les fait converger vers le foyer image ; c'est le rayon rouge de mes dessins ; après avoir traversé la lentille il passe par le foyer image F₁'
. la distance focale d'une lentille divergente est négative ; ici
. les rayons qui arrivent parallélement à l'axe optique sur une lentille divergente, après avoir traversé la lentille, divergent depuis le foyer image : c'est le cas du rayon bleu du deuxième dessin ; après la lentille il semble provenir du foyer image F₂'
. aussi bien pour une lentille convergente que pour une lentille divergente, un rayon qui passe par le centre optique n'est pas dévié ; c'est le cas du rayon vert pour le premier dessin et du rayon rouge pour la deuxième lentille dans le deuxième dessin
. pour une lentille convergente, un rayon qui passe par le foyer objet sort de la lentille parallélement à l'axe optique ; c'est le cas du rayon bleu pour la première lentille.

Je t'ai rappelé plus haut la loi de conjugaison, qui doit obligatoirement être appliquée avec les mesures algébriques.

Fais cela et tu n'auras plus de difficulté avec l'optique géométrique.

BONJOUR,

Merci pour tes explications claires et pour m'avoir accordé un peu de ton temps .
Passe un bon réveillon de fin d'année et rendez-vous en 2013.

Encore merci.


Cordialement

Je te souhaite à toi aussi "une bonne fin d'année"...
____________

Mais je reste disponible pour bien terminer cet exercice.
Tu as les deux schémas, j'aimerais savoir si tu es d'accord avec l'un comme l'autre.
J'aimerais aussi que tu saches confirmer par le calcul la position de l'image finale A₂B₂

Bonsoir et bonne année,

je ne trouve pas comme toi pour A2', je trouve -0,09 ou -0,1
avec O2F2=0,1 et O2A1=-1,3
Ce qui me donne une image bien differente de la tienne .
J'ai au final O2A2'à 0,1.
Comment as-tu trouvé -O,45 pour O2A2' ?

En revanche je suis d'accord avec le premier schéma .

Merci

Première lentille
Elle est convergente, de distance focale 0,30 m
Son centre optique O₁ est pris comme origine des abscisses sur l'axe optique
Elle donne de l'objet AB une image A₁B₁

Formule de conjugaison pour une lentille mince de centre O₁, formule dite de Descartes
Le pied de l'objet est en A
Le pied de l'image est en A₁
Le foyer image est en F₁'
L'axe optique est orienté (dans le sens de propagation de la lumière)



Or ici :

et


et donc



______________

Deuxième lentille
Elle est divergente, de distance focale -0,10 m
Son centre optique O₂ est à l'abscisse 0,30 m
Elle donne de l'objet (virtuel) A₁B₁ une image A₂B₂



Or ici :

et


et donc



C'est-à-dire que le point A₂ a pour abscisse 0,30 - 0,45 = -0,15 m (comme sur la figure que j'ai faite ! )

Décidement j'étais encore a coté de la plaque je n'ai pas pris en compte les valeurs de de la lentille L1 je suis partie sur les valeurs de la lentille L2 seule.

Je vais completer mes cours par des livres que je vais acheter sinon quand ça va se compliquer se sera dur dur.

L'image A₁B₁ donnée par la lentille L₁ devient l'objet pour la lentille L₂