Niveau seconde

Hauteur max que peut atteindre une skieuse

Posté par
hormijo 28-10-17 à 18:55

Bonjour, je cale complètement sur cet exercice.. Voici l'énoncé :

"Lors d'une compétition de planche à neige, une planchiste descendant une pente à une
vitesse de 45 km/h prend un saut de 2 m de haut. À quelle hauteur maximale la planchiste, dont la vitesse était de 45 km/h, peut-elle espérer atteindre si le saut qu'elle prend possède une hauteur de 2 m et une inclinaison par rapport à l'horizontale de 55° (négligez le frottement)?"

merci d'avance

Posté par re : Hauteur max que peut atteindre une skieuse 29-10-17 à 08:13

Hello

Ci dessous ce que je crois comprendre de ton énoncé (peut être limpide pour un planchiste ... pas tant que cela pour un physicien)

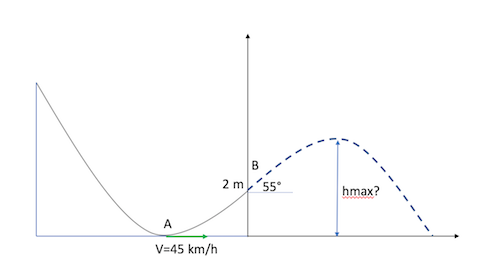
La skieuse passe en A avec une vitesse de 45 km/h, puis remonte sur le piste une hauteur de 2 m jusqu'au point B où elle s'envole, sa trajectoire en ce point formant un angle de 55° par rapport à l'horizontale?

Et on demande la hauteur max atteinte?

Est ce cela?

Hauteur max que peut atteindre une skieuse

Posté par re : Hauteur max que peut atteindre une skieuse 29-10-17 à 12:31

A vrai dire ça me rassure de voir que je ne suis pas la seule à trouver l'énoncé pas clair.. C'est un exercice que j'ai trouvé sur internet pour m'entraîner, votre schéma me parait bien , mais je serai incapable de dire avec certitude (d'autant plus que la physique c'est pas trop mon truc)

Mais si on considère que c'est bien ça j'avoue que je ne vois pas plus comment le résoudre..

Posté par re : Hauteur max que peut atteindre une skieuse 29-10-17 à 17:01

Alors je te propose la méthode suivante (je décompose en 2 étapes pour "ne pas te perdre")

Dans un premier temps calculons la vitesse au moment du décollage (en B donc):

Pour cela appliquons le théorème de l'énergie cinétique:

L'énoncé nous indique que les frottements sont négligeables, donc seul le poids travaille (à par nous bien sûr ... )

Et le poids étant une force conservative, elle dérive d'un potentiel (l'énergie potentielle de pesanteur), et son travail est égal à la dimunition de l'énergie potentielle:

Donc $\Delta E_c = \frac{1}{2}mV^2_B - \frac{1}{2}mV^2_A= W(\vec{P})= Ep(A) - Ep(B) = mgz_A - mgz_B = -mgh_1$

Donc     $V_B = \sqrt{V_A^2 - 2gh_1}$         (h₁ = 2 m)

Interessons nous maintenant à la seconde partie du parcours

Et appelons S le sommet de la trajectoire:

Entre B et S la composante horizontale de la vitesse se conserve
Par contre en S la composante verticale est nulle  (c'est le sommet)

Donc $V_S = V_B.cos\theta$    (avec = 55° )

Appliquons à nouveau le théorème de l'énergie cinétique entre B et S:

Donc $\Delta E_c = \frac{1}{2}mV^2_S - \frac{1}{2}mV^2_B= W(\vec{P})= Ep(B) - Ep(S) = mgz_B - mgz_S = -mg(h_{max}-h_1)$

$V^2_S - V^2_B = -2g(h_{max}-h_1)$

$V_B^2sin^2\theta = 2g(h_{max}-h_1)$

Soit

$h_{max} = h_1cos^2\theta + \frac{V_A^2}{2g}sin^2\theta$

Sauf étourderie .... dont je suis familier

Posté par re : Hauteur max que peut atteindre une skieuse 31-10-17 à 19:52

Bonsoir à tous,

@hormijo : dernier avertissement avant une exclusion définitive : prière de te désinscrire du compte josephineEG.

A bon entendeur ...

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau seconde
49 fiches de physique - chimie en seconde disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Hauteur max que peut atteindre une skieuse

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique