Inscription / Connexion Nouveau Sujet
force centrale : question de cours
salut mes amis
dans un bref rappel de cours on a fait
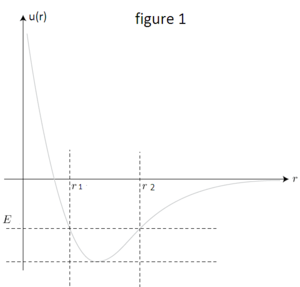
une particule en mouvement dans champs de force centrale la variation de l'énergie potentiel : figure 1
si E<0  n obtient un mouvement oscillatoire et la trajectoire est comprise entre entre 2 cercle de rayon r1 et r2 avec r1 et r2 les racine de l'équation E=u(r)
n obtient un mouvement oscillatoire et la trajectoire est comprise entre entre 2 cercle de rayon r1 et r2 avec r1 et r2 les racine de l'équation E=u(r)
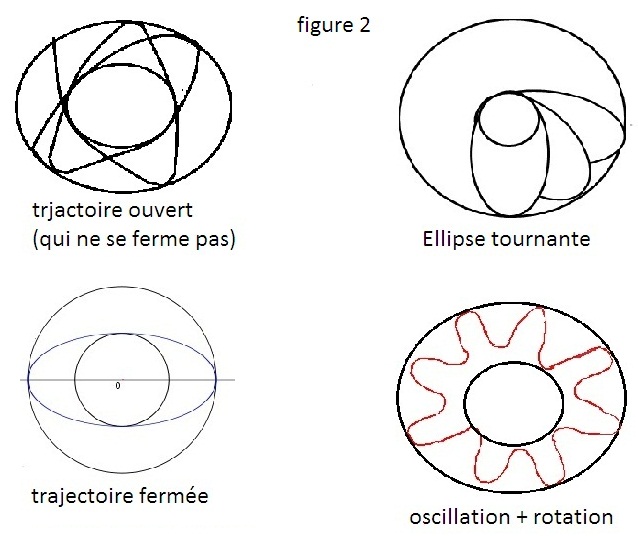
si le mouvement est dans le plan la trajectoire peut être : figure 2
un coup de main pour comprendre ce sujet s'il vous plait
Bonjour
Tu peux consulter le document suivant, en particulier V.5
N'hésite pas ensuite à poser des questions complémentaires
Bonsoir Vanoise
merci pour la réponse
merci pour le document
moi ce que je sais avant que :
si E>0: c'est l'état libre la trajectoire est hyperbole ou parabole
si E<0 : c'est l'état lié la trajectoire est une ellipse
le cas E<0 c'est le cas qui devient compliqué car la trajectoire ellipse devient (après le résumé mentionné ci dessus) un cas particulier et que le cas le plus général c'est que la trajectoire comprise entre 2 cercles de rayons r1 et r2
on peut déterminer r1 et r2 par la résolution de l'équation E=U(r)
mais comment déterminer la nature de la trajectoire si c'est une ellipse tournante ou trajectoire ouvert ou on oscillation + rotation
je reformule mon problème d'une autre façon :
je prend le cas particulier : la trajectoire est une ellipse tournante
je veux un exemple de mouvement
le type de la force centrale est ce que de type ou un autre type
l'équation de la trajectoire c'il est possible ...
Quelques précisions :
1: A propos de la courbe représentée : U(r) ne représente pas l'énergie potentielle Ep mais l'énergie potentielle effective : somme de l'énergie potentielle et du terme de l'énergie cinétique ne dépendant que de r. Voir pour cela le paragraphe IV de mon document sur les formules de Binet et le paragraphe V.5 sur l'énergie potentielle effective que je note Ep(eff). Puisque ainsi l'énergie mécanique devient :
.
Le terme étant positif ou nul, on obtient :
ce qui limite les valeurs de r comme tu l'as indiqué.
2. La loi des aires est valide ; la trajectoire est nécessairement plane.
3. En revanche, la trajectoire n'est une conique que pour les forces centrales en 1/r2 : forces centrales gravitationnelles et électrostatiques.
4. Si tu veux l'équation de la trajectoire pour une force centrale autre, tu peux appliquer la relation fondamentale de la dynamique à la particule en utilisant ton expression de la force et la deuxième formule de Binet : voir paragraphe 5.2.
Tu trouveras sur wikipedia quelques informations générales sur le cas des forces en - k.rp.
Outre le très classique p=-2 , on traite souvent le cas p=1 : force élastique. Il y a aussi quelques études du cas p=3 et du cas p=0.
Merci Vanoise pour l'explication et l'indication
je veux savoir seulement :
le mouvement de la particule dans un champ de force centrale(en prend comme exemple le cas p=2)
si la trajectoire est fermé
est ce que fermé signifie que c'est une ellipse
est ce que le mot ellipse dans ce cas englobe l'ellipse constante et l'ellipse tournante
Dans le cas p=2, la trajectoire est une conique :
Il s'agit d'une ellipse dans le cas où l'énergie mécanique est négative avec les conventions usuelles sur le niveau zéro de l'énergie potentielle. L'ellipse est alors fixe dans un référentiel galiléen.
Bonjour
Merci Vanoise
j'ai des question de base
1- est ce que les phrases sont équivalent
-un point matériel est soumis a une force centrale
-un point matériel est dans un puits de potentiel
-un point matériel est dans un champ de force
2-on peut considère le mouvement de pendule(ou en générale le mouvement circulaire) comme un mouvement de force centrale
3-comment différentier entre une force centrale conservative et une force centrale non conservative
Question 1 :
Force centrale : si O est un point fixe de l'espace, le point matériel M est soumis en toute position à une force colinéaire au vecteur OM.
Puit de potentiel : l'énergie potentielle présente un minimum pour une position donnée. Cette position est une position d'équilibre stable.
Un champ de force est une région de l'espace où le point M est soumis à une force exercée à distance par la source du champ.
Un même problème peut faire intervenir simultanément ces trois notions mais celà n'a rien d'obligatoire.
Question 2 : la masse d'un pendule simple en absence de frottement est soumise à deux forces. La tension du fil qui est une force centrale et son poids qui n'est pas une force centrale.
Question 3 :
Une force centrale est conservative seulement si la norme du vecteur force ne dépend que de la distance r=OM, surtout pas de la vitesse.
Question message précédent :
Tu as évoqué les ellipses tournantes. A ma connaissance, il n'existe pas de force en k.rp capable de produire un tel mouvement. En revanche, imagine un mouvement elliptique sous l'action d'une force centrale attractive en k/r2. En ajoutant à cette force de faibles perturbations, notamment une force en k'/r3, il est possible d'obtenir un lent mouvement de rotation du vecteur de Lenz (voir mon document déjà signalé )
Mes réponses sont brèves. N'hésite pas à poser des questions précises complémentaires si tu le juges utile.
Bonjour,
Merci Vanoise pour ces explication
je me laisse dans le cas ou
si on applique la relation fondamental de dynamique
avec le 2ème formule de Binet
la solution de cette équation différentielle est
comment déterminer A et
si on considère que les condition initiale de mouvement à t=0 :
et
La valeur de  doit aussi être connue à l'instant initial.
doit aussi être connue à l'instant initial.
Les données permettent d'obtenir le moment cinétique au point O ainsi que la constante des aires C.
Tu peux utiliser les équations que tu as écrites et en plus : la première formule de Binet (voir paragraphe IV du document déjà fourni) sur le vecteur vitesse.
Le calcul est très simple dans le cas où, à la date t=0, le vecteur vitesse et le vecteur position sont orthogonaux. La position initiale correspond alors soit au périastre, soit à l'apoastre ;  est alors égal soit à zéro soit à
est alors égal soit à zéro soit à  rad.
rad.
Merci Vanoise pour la réponse
j'arrive pas à résoudre le problème, mais quand même je partage mes tentatives
les condition initial :
à t=0 :
( La position initiale correspond au périastre)
donc
les constantes de mouvement
*la constante des aires :
je ne sais pas si comme le mouvement circulaire on a
* le moment cinétique (en module):
*l'énergie mécanique :
l'équation de mouvement est :
à t=0 :
c-a-d :
je ne sais pas si cette formule est homogène
si on on utilise la première formule de Binet :
on a
à t=0 on a
c-a-d
Quelques remarques...
1° : Tu considères a priori que l'état initial correspond au périastre, ce qui te permet de poser . Tout dépend de la valeur de vo ! Si voc désigne la vitesse initiale correspondant au mouvement circulaire uniforme, on peut poser :
où  est un réel positif ou nul. En raisonnant, par exemple sur l'énergie potentielle effective, on peut montrer :
est un réel positif ou nul. En raisonnant, par exemple sur l'énergie potentielle effective, on peut montrer :
*si la trajectoire est une branche d'hyperbole ;
* si la trajectoire est une parabole ;
* si } la trajectoire est une ellipse, l'état initial correspondant au périastre ;
*si la trajectoire est une ellipse, l'état initial correspondant à l'apoastre. Bien sûr : pour
 proche de 0 par valeur supérieure, le satellite peut éventuellement entrer dans l'atmosphère de l'astre et s'écraser sur celui-ci...
proche de 0 par valeur supérieure, le satellite peut éventuellement entrer dans l'atmosphère de l'astre et s'écraser sur celui-ci...
* si la trajectoire est une droite.
Donc, sans plus de précision,
2° Le moment cinétique du satellite en O a pour expression : . Si on passe aux normes, cela ne donne Lo=m.r.v que si les vecteurs vitesse et position sont orthogonaux, donc seulement au périastre et à l'apoastre. Tu peux donc poser :
et
3° L'énergie mécanique s'écrit :
Attention au signe ; pour une trajectoire fermée, l'énergie mécanique est négative.
4° Pour l'obtention de l'équation de la trajectoire sous la forme :
tu peux aussi utiliser la première formule de Binet sous la forme :
ah bon,
moi je croix avant que est égale à
donc si je comprend bien
l'état initial est dépend au vitesse initiale et au position initial
(comme si on fait l'analogie avec le mouvement oscillatoire avec vitesse et position initial)
*y-a t-il une formule générale qui permet de calculer dans le cas ou
est quelconque
*est ce que le traitement concerne la constante A dans mon message précédent est correcte?
*j'ai une petit difficulté pour obtenir l'équation de mouvement a partir de l la première formule de Binet :
on a deux axe dans la formule et
quel est l'axe utiliser pour la projection
Dans le cas particulier où la position initiale est le périastre ou l'apoastre, l'axe des abscisses étant ainsi le grand axe de l'ellipse, l'équation générale de la trajectoire conduit à :
Dans le cas général, la première formule de Binet s'écrit :
avec :
Soit :
A la position initiale :
Dans le cas particulier où la position initiale est le périastre ou l'apoastre, la vitesse initiale, nécessairement tangente à la trajectoire, n'a pas, dans ce cas particulier de composante suivant . Cela implique :
Si :
; la position initiale est le périastre.
Si :
; la position initiale est l'apoastre.
Sinon : l'application de la relation fondamentale de la dynamique combiné à la deuxième formule de Binet conduit à l'expression de p (voir §V.2 de mon document). L'expression générale de l'énergie mécanique permet d'obtenir l'excentricité (voir §V.3 du même document) mais il y a plus simple ici : la première formule de ce message permet d'obtenir e, une fois p connu.
Bonsoir Vanoise,
c'est clair maintenant merci
dans le document mentioné il y a (la formule est démontré)
avec
et
et
donc on peut determiner p et e
et à l'aide de
on peut déterminer
mais le problème est encore persiste si on suppose si la particule ne se trouve pas dans le grand axe de l'ellipse ici le paramètre s'intervient:
ici il y a deux cas (je suppose, mais je ne suis pas sûr)
-on choisir arbitrairement ce qui implique que la particule est n'est pas dans l'orbite
-on ne choisi pas ce qui implique que la particule se trouve sur l'orbite et
lié avec
avec la relation :
ce qui ajoute un autre inconnu
Dans le cas le plus général : si  =
= , alors :
, alors :
L'angle polaire  est donc l'angle polaire correspondant au périastre P. Si tu préfères :
est donc l'angle polaire correspondant au périastre P. Si tu préfères :
.
Si tu veux traiter le problème le plus général, tu peux imaginer qu'à la date t= 0, M occupe la position Mo telle que avec une vitesse initiale
telle que :
Il te faut alors déterminer les trois inconnues p, e et  . C'est un peu "calculatoire"...
. C'est un peu "calculatoire"...
Bon journée
Merci Vanoise de m'avoir accorder du temps
je vais continuer l'étude de ce cours et traiter les autres cas
je reviens si je rencontre des difficultés
merci
Bonsoir Vanoise
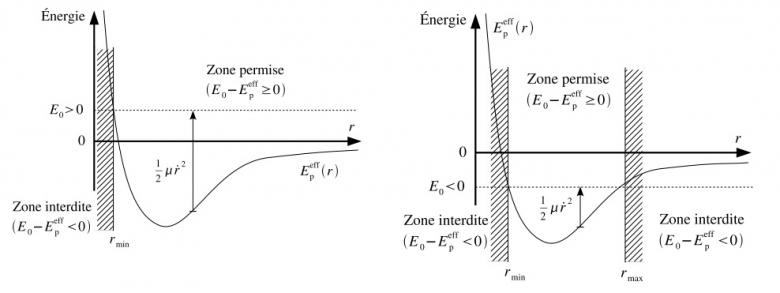
je veux seulement savoir qu'est ce qu'on désigne par la zone interdite dans le schéma suivant ?
est ce qu'on désigne que si r_0<r_{min} ou r_0>r_{max} et quoique la vitesse fournie au particule il reste immobile ?
J'ai partiellement répondu à ta première question dans mon message du 16-02-21 à 18:02. Puisque de façon générale, pour une force centrale :
et puisque le terme est positif ou nul, on obtient :
. Toutes les valeurs de r telles que
sont des valeurs interdites pour le mouvement. C'est ce qu'illustrent les schémas que tu fournis dans ton message précédent mais aussi le schéma de ton premier message et les schémas du paragraphe V.5 du document que je t'ai indiqué précédemment.
Reprends les expressions de Em et de Ep(eff). Il est impossible d'avoir Em<Ep(eff). Il faut bien comprendre ce qu'est l'énergie potentielle effective, à bien différentier de l'énergie potentielle.
Merci Vanoise de votre réponse
vraiment j'ai une difféculté à comprendre
Je parle sur l'état ou mais r_o qui représente la position initiale
Je veux comprendre le mot interdite
Si r_ou
il n y a pas de mouvement et le particule reste immobile
Ou on ne peut pas placer le particule dans ces position c est à dire le mouvement échoué comme l'exemple d une satellite il ne prend pas son orbite et revient à la terre
Ou.....
Dans ce contexte, « interdit » signifie « impossible à obtenir physiquement ». Je t'ai déjà fourni une démonstration de cela. La cause de ton incompréhension vient peut-être d'une mauvaise compréhension de ce qu'est l'énergie potentielle effective. L'énergie potentielle, pour un astre attracteur donné, ne dépend que de r, donc que de la position du satellite quasi ponctuel M. En revanche, l'énergie potentielle effective dépend à la fois de r et des conditions initiales. Je veux bien reprendre pas à pas la démonstration en prenant comme conditions initiales, celles définies en fin de mon message du 25-02-21 à 19:16.
La constante des aires vaut :
L'énergie mécanique vaut :
Nous allons la supposer négative de façon à obtenir une trajectoire elliptique. L'énergie potentielle effective est :
On voit bien que, comme écrit en introduction, cette énergie potentielle effective dépend de ro et vo, donc des conditions initiales et de r.
Comme déjà écrit, les valeurs possibles de r doivent correspondre à . Les valeurs limites rmin et rmax sont les solutions de l'équation du second degré :
soit :
avec Em<0.
La suite est un peu calculatoire ; on vérifie que dans tous les cas :
ro ne peut pas physiquement appartenir aux zones interdites...
Remarque : le cas a=90° est le cas étudié dans les premiers messages. L'axe des x porte alors le grand axe de l'ellipse. Si rmin=ro : la position initiale est le périastre ; si rmax=ro : la position initiale est l'apoastre.
Bonsoir Vanoise
j'ai besoin de votre aide dans un problème lié a ce sujet :
une particule se déplaçant sur un axe Or et soumise à un potentiel V (r) représenté
à la figure suivante. On veut étudier qualitativement le mouvement de la particule pour différentes valeurs de son énergie mécanique. Pour chacun des cas suivants décrire qualitativement le mouvement puis tracer l'allure de r(t) et de .
1.Pour avec
et
.
2. Pour avec
et
.
3. Pour avec
et
.
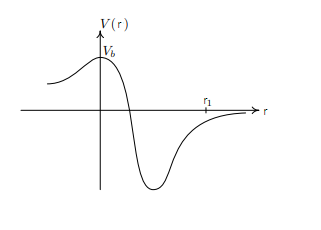
je procède comme suit :
d'abord je propose que le mouvement et rectiligne donc pas de variable on travail sur une seule variable qui est r
donc on a hors la zone interdite et l'énergie mécanique est supérieur à l'énergie potentielle effective
1 ère cas : Pour avec
et
.
on a dans l'état lié, la trajectoire est borné entre 2 valeur et
qui sont les solutions de l'équation
et on a :
et je me bloque, je ne sais pas qu'est ce que signifie et comment l'exploiter dans l'équation de mouvement
Remarque préliminaire : l'expression V(r) désigne en réalité l'énergie potentielle que l'on note souvent aussi Ep(r). Pas d'énergie potentielle effective dans ce problème à une dimension. Puisque :
Em(r)=V(r)+½m.v2 , les valeurs de r possibles vérifient :
1er cas :
Puisque l'énergie cinétique initiale est positive et que l'énergie mécanique est négative, on obtient en réalité :
: cela signifie que la particule part dans le sens des r négatifs jusqu'à une position rmin à déterminer où la vitesse s'annule puis repart en sens inverse jusqu'à une position rmax à déterminer aussi. Bref : la particule va osciller dans le puits de potentiel en absence de frottement.
Bon journée
Merci Vanoise pour l'explication
le 2ème cas : le particule est dans l'état libre, il dans une mouvement rectiligne avec une énergie initiale E_m-V(r) jusqu'à l'arrive à
est s'arrête
le 3ème cas :
pas de potentiel ici, le particule est dans un mouvement rectiligne uniforme avec une énergie initiale
Pas d'accord avec ton dernier message aussi bien pour le cas 2 que pour le cas 3. Cela laisse penser que tu n'as peut-être pas compris de façon approfondie le cas 1. Pour t'aider, je te poste quatre simulations.
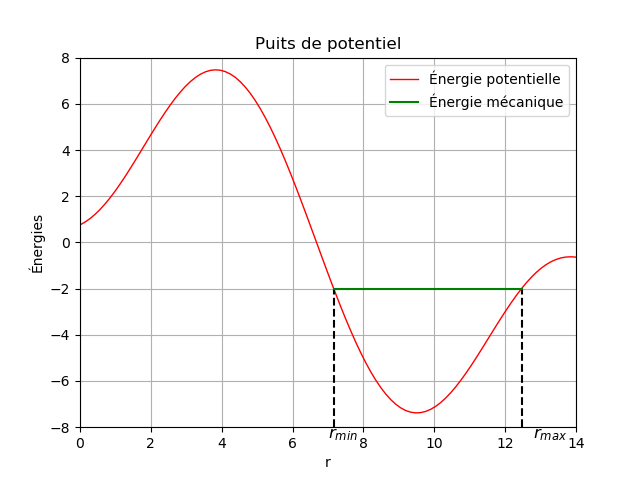
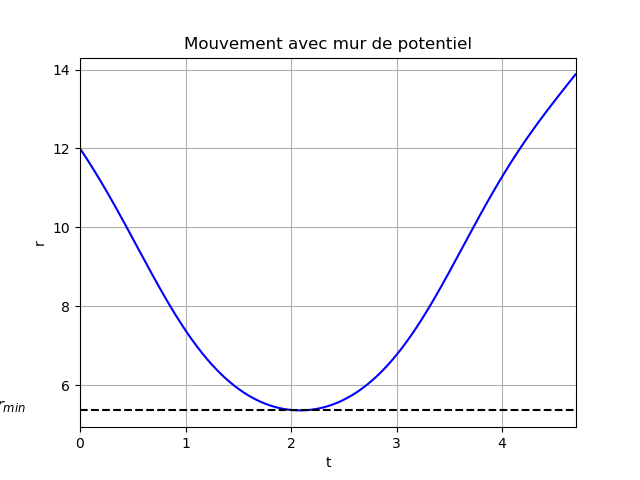
J'ai reconstitué approximativement l'allure de la courbe V(r) et je prends les conditions initiales suivantes :
Em=-2 ; r(0)=12 ; v(0)<0. (Unités et échelles totalement arbitraires...)
La figure 1 visualise rmax et rmin.
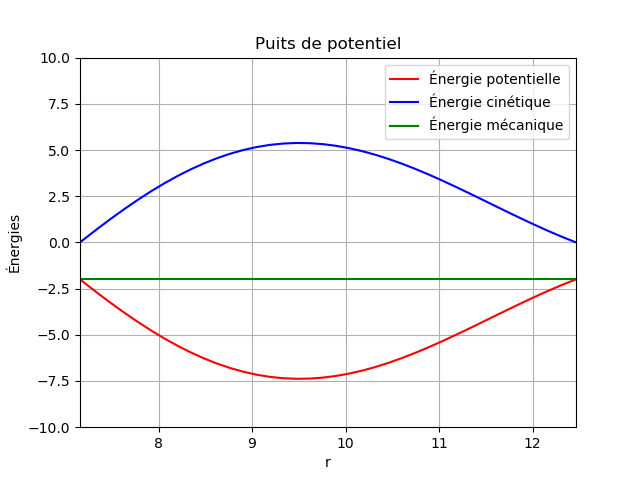
La courbe 2 est un "zoom" représentant les variations des trois énergies en fonction de r.
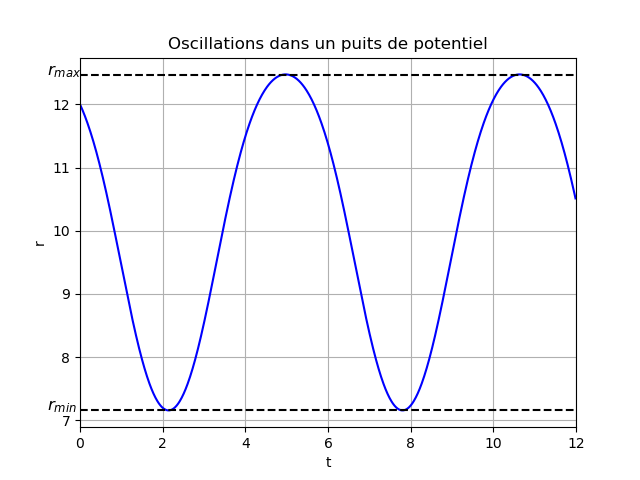
La courbe 3 représente r=f(t)
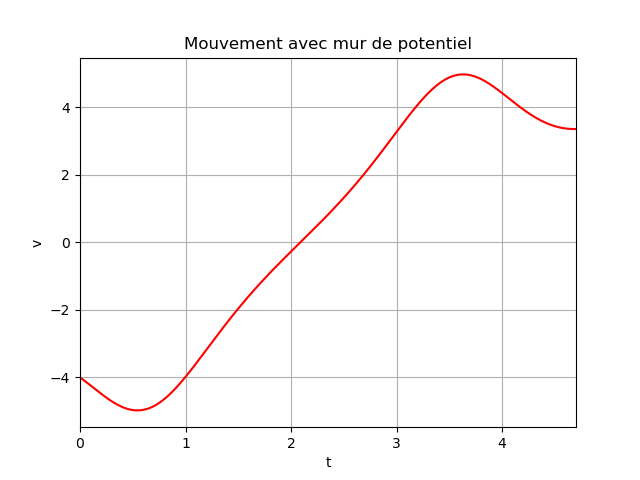
La courbe 4 représente v=f'(t).
Si la courbe V(r) était assimilable à une branche de parabole entre rmin et rmax, nous aurions un oscillateur harmonique...
Merci Vanoise
pour le 1er cas je pense que c'est clair,
si je ne trompe pas, la particule est confiné, oscille entre et
mouvement rectiligne aller retour
,
est constante
donc la vitesse est variable parce que le puits de potentiel est variable
si le puits est sinusoïdale le mouvement( la variation de r(t)) ainsi la vitesse est sinusoïdale
si le puits est constante la vitesse est constante .
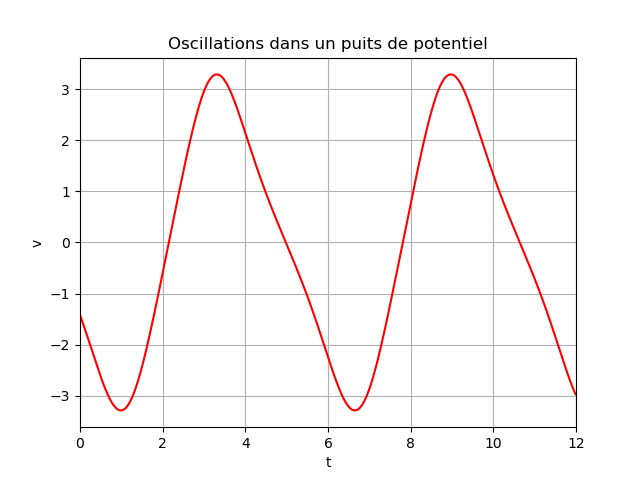
si le puits a une autre variation, la vitesse subit l'inverse de cette variation (figure 2 )
pour les 2 autres cas vraiment je ne sais pas
si le puits est sinusoïdale le mouvement( la variation de r(t)) ainsi la vitesse est sinusoïdale
Non : un mouvement rectiligne sinusoïdal correspondrait à un oscillateur harmonique. Entre rmin et rmax, la courbe rouge Ep=V(r) et la courbe bleue Ec(r) de la deuxième figure seraient des arcs de parabole.
En r=rmin, la vitesse s'annule mais la force appliquée à la particule : F=-(dV/dr) est strictement positive, la particule repart dans le sens positif.
En r=rmax, la vitesse s'annule mais F=-(dV/dr) est strictement négative, la particule repart dans le sens négatif, d'où les oscillations.
Si tu as bien compris tout cela, reprend le cas n° 2 ; dessine au besoin l'allure de la courbe Ec= f(r) et intéresse-toi à l'expression de la force en r=rmin...
Bonsoir Vanoise
Donc dans le 2eme cas(si je comprend bien)
Le particule faire départ de vers
la vitesse s'annule puis le particule repart vers l'infini (comme un mouvement hyperbolique)
l'énergie mécanique est constante, la courbe de l'énergie cinétique s'obtient comme l'image de la courbe de V(r) par rapport l'axe
Je crois que tu as bien compris maintenant. En conservant la même allure du potentiel que précédemment et en choisissant comme conditions initiales :
Em=5 ; r(0)=12 ; v(0)<0. (Unités et échelles totalement arbitraires...), on obtient pour r(t) et v(t) les courbes suivantes. En supposant que l'énergie potentielle reste fixe pour r
 , quand t devient grand, la courbe r(t) devient assimilable à une droite oblique et v(t) devient une constante.
, quand t devient grand, la courbe r(t) devient assimilable à une droite oblique et v(t) devient une constante.
Merci Vanoise,
Je continue pour le 3 ème cas:
Ici il n y a pas de barrière de potentiel, donc pas de , la particule part vers les r négatifs avec une énergie cinétique symétrie à V(r) par rapport à
, quand il n y pas de potentiel la vitesse est constante.
D'accord avec ton message. Je modifierais la fin de ta phrase de la façon suivante : "quand l'énergie potentielle devient constante, la vitesse devient constante".
Bonjour Praf, bonjour Vanoise,
Merci pour cet Exo et ces explications très intéressantes !
- Une précision pour Praf par rapport à son message du 04/03/21 à 17h45 et la racine carrée d'une expression :
on a : Em = (1/2)*m*(dr/dt)^2 + V(r)
on en déduit : (dr/dt)^2 = (2/m)*(Em - V(r))
d'où : (valeur absolue de dr/dt ) = [ (2/m)*(Em - V(r)) ]^(1/2)
et comme on nous dit que dr/dt (0) < 0, et que r(0) = r1,
on a dr/dt(0) = - [ (2/m)*(Em - V(r1)) ]^(1/2)
(mathématiquement, on s'y retrouve, la racine carrée d'un nombre est toujours positive ou nulle )
Bonsoir Vanoise
revenant a votre message 20-02-21 à 22:49 , dans l'explication concerne l'ellipse tournante
un mouvement elliptique sous l'action d'une force centrale attractive en k/r2. En ajoutant à cette force de faibles perturbations, notamment une force en k'/r3, il est possible d'obtenir un lent mouvement de rotation du vecteur de Lenz
j'ai un exercice sur ce problème, mais j'ai des des difficultés a le résoudre:
Une particule de masse m se déplace avec un moment cinétique L dans un champ de force central
les constantes k et
1- Montrer que l'orbite est de la forme :
ou p, e et
2- déterminer p, e et
un coup de main s'il vous plait pour commencer
les force sont conservatives donc les constantes de mouvement sont E et L
dans ce cas est ce qu'il y a une constantes des aires C ?
est ce qu'on peut appliquer la formule de Binet ?
L étant connu ainsi que m, C est connu. La relation fondamentale de la dynamique appliquée en utilisant la seconde formule de Binet conduit à une équation différentielle très simple vérifiée par (1/r) fonction de  .
.
Tu peux t'inspirer du paragraphe V.2 de mon document dont je t'ai fourni la référence. Il suffit d'adapter un peu...
salut Vanoise,
La relation fondamentale de la dynamique appliquée en utilisant la seconde formule de Binet conduit à :
ce qui donne si on pose
quel est la solution de cette équation différentielle ?
Reprends le document dont je t'ai fourni la référence. A condition de remplacer "1" par
, l'étude est identique.
D'accord puis passe à l'équation classique de la conique. Ton énoncé suppose sans le dire vraiment que l'angle polaire nul correspond au périastre.
l'équation de conique est sous la forme (si je ne trompe pas dans les calcules)
j'arrive pas à trouver le facteur de
dans l'énoncé
Je repars de l'équation différentielle du second ordre :
Solution particulière :
Solution de l'équation homogène :
Je te laisse continuer...
Bonsoir Vanoise,
Merci pour l'explication, maintenant je comprend bien, l'équation différentielle obtenu si on fait l'analogie c'est comme l'équation différentielle d'un oscillateur harmonique avec frottement solide
on a
le reste des question
-décrivez l'orbite dans le cas 0 < e< 1.
2-Pour quelles valeurs de β l'orbite est-elle fermée ?
3- Que deviennent vos résultats si → 0 ?
4-Comme la perturbation est faible (α petit), le paramètre est proche de l'unité. Expliquez pourquoi la courbe correspond à une ellipse en précession, c'est-à-dire dont l'orientation change dans le temps.
je pense que dans le cas ou 0<e<1 l'orbite est une ellipse
pour que l'orbite est fermée je pense que doit égale à 1
mais les autres questions j'ai besoin de l'aide
pour une ellipse en précession supposons que est l'angle qui fait l'axe de l'ellipse avec l'axe polaire, la précession (pour moi, si je comprend bien) est une modification de
dans le temps
pour un mouvement uniforme
mais ici est constante donc l'incohérence pour moi
Tu peux poser  =0 si la position =0 correspond à un passage au périastre. D'accord avec tes résultats.
=0 si la position =0 correspond à un passage au périastre. D'accord avec tes résultats.
Pour montrer la précession, il y a une méthode simple.
Puisque , tu peux poser :
avec
(développement limité au premier ordre de la racine carrée). Ainsi :
Tu peux déterminer les valeurs successives de t pour lesquelles r= rmax (apoastre). comment évoluent ces différentes valeurs de  en fonction du nombre de tours ? Pour visualiser cela, tu peux jeter un coup d'il à la fin du document que je t'ai indiqué précédemment. J'y ai rajouté une petite animation au format mp4. Elle n'est pas encore tout à fait au point mais on voit bien tout de même l'évolution de la trajectoire. Les positions successives sont prises à intervalles de temps successifs égaux, ce qui permet d'illustrer la loi des aires : le satellite se déplace nettement plus vite au voisinage du périastre que de l'apoastre.
en fonction du nombre de tours ? Pour visualiser cela, tu peux jeter un coup d'il à la fin du document que je t'ai indiqué précédemment. J'y ai rajouté une petite animation au format mp4. Elle n'est pas encore tout à fait au point mais on voit bien tout de même l'évolution de la trajectoire. Les positions successives sont prises à intervalles de temps successifs égaux, ce qui permet d'illustrer la loi des aires : le satellite se déplace nettement plus vite au voisinage du périastre que de l'apoastre.
Attention : faire intervenir le temps est particulièrement délicat, même pour  =1. Cela demande de résoudre l'équation de Képler qui n'admet pas de solution littérale. Il faut se contenter d'une résolution numérique. C'est peut-être pour cela que les programmes de physiques, sauf dans les spécialisations en astronomie, ne demande jamais d'étudier r et
=1. Cela demande de résoudre l'équation de Képler qui n'admet pas de solution littérale. Il faut se contenter d'une résolution numérique. C'est peut-être pour cela que les programmes de physiques, sauf dans les spécialisations en astronomie, ne demande jamais d'étudier r et  en fonction du temps.
en fonction du temps.
Bonjour,
Une question à Vanoise : "pour quelles valeurs de b l'orbite est elle fermée ?" :
N'y a t-il pas d'autres valeurs que b =1 ?
- la fonction cos(b*teta - phi) est de période 2*pi/b ; s'il existe des entiers n et q tels que : n * 2*pi/b = q*2*pi ; c'est à dire si b = n/q ;
Alors l'orbite est fermée aussi, non ?