Quand est différent de 1, la trajectoire n'est pas fermée  : voir l'animation en fin de document. Si très inférieur à 1, la trajectoire est très peu déformée par rapport à l'ellipse correspondant à =1. On peut décrire la trajectoire comme une ellipse qui tourne très lentement autour du point O dans le plan fixe perpendiculaire au vecteur moment cinétique.
Pour trouver la période de rotation, tu peux t'intéresser aux valeurs successives de qui correspondent à rmax.  Elles vérifient  :
(1+)=+2n où n est un entier positif.
Rappel : pour très petit devant 1 :
(1+)^-11-

Bon jour,
j'arrive pas à résoudre le problème
dans ce cas particulier, on parle sur deux période :
- période de mouvement sur l'ellipse : il obéit  a la 3eme loi de Kepler  :

        

avec a le demi grand axe de l'ellipse
on peut démontrer cette formule on utilisant la loi de vitesse aréolaire comme il a mentionné dans le document  

-période de rotation de l'ellipse : je suppose qu'elle dépend de l'angle de rotation  après que la particule termine un tour sur l'ellipse, donc je suppose que je dois calculer et je ne sais pas comment

est la variation de quand n augmente d'une unité ce qui correspond à une durée d'un tour soit la durée Tr. Je t'ai expliqué dans mon message précédent la méthode pour obtenir

excuse moi Vanoise,

est ce que?

Laisse en fonction de n et utilise l'approximation que je t'ai indiquée.

Merci Vanoise,
Maintenant je comprend bien.
La variation de  en rmax est donné par



Pour le nombre de tour effectuée par l'ellipse pour revient à sa position initiale est ce qu'on peut faire:



Avec ici   l'augmentation de d'une unité

En un tour, n augmente d'une unité, la variation de correspondante est donc :

Imaginons que l'on obtienne . Le grand axe de l'ellipse aurait tourné exactement d'un tour. Le périastre reprendrait la même position qu'au tour précédent. La trajectoire serait fermée ; cela correspondrait à la situation en absence de perturbation. En présence de la perturbation, le demi grand axe tourne d'un peu moins d'un tour :

avec

Pour un observateur, le grand axe de l'ellipse semble tourner lentement dans le sens rétrograde autour du centre de l'astre attracteur de par période de rotation, ce qui correspond à une vitesse angulaire dans le sens rétrograde de valeur absolue :

Merci Vanoise pour ces explication,
Est ce qu'on peut faire :

Dans mon dernier message, je n'ai pas utilisé les même notations que toi. Je reprends en prenant tes notations en compte :

Te = période du mouvement elliptique en absence de perturbation, valeur donnée par les lois de Kepler ;

Tr = période de rotation du grand axe de l'ellipse, où, pour être plus rigoureux : période de rotation du vecteur de Lenz autour du centre O de l'astre attracteur.

Ce vecteur tourne dans le sens rétrograde (sens négatif de mon document) de pendant la durée Te (et non Tr comme écrit hier).

La vitesse de rotation du grand axe de l'ellipse est ainsi en valeur absolue :





Cela conduit simplement à :



Puisque :

Merci Vanoise.
C'est clair maintenant.

Bonsoir Vanoise,

je me bloque dans l'étude de force F=kr.
La relation fondamentale de la dynamique appliquée en utilisant la seconde formule de Binet conduit à :



donc



quel est la résolution de cette équation ?

Mouvement plan, loi des aires, tout cela est valide ici. Pour le reste, il est préférable de partir de :

  
et de projeter la relation sur les deux axes d'un repère cartésien. Tu vas obtenir deux équations différentielles indépendantes aux solutions très simples. Tu va obtenir comme trajectoire une ellipse de Lissajoux.
Par la même méthode, tu peux étudier la situation, avec k>0 :

même si je n'en vois pas trop d'applications pratiques.

Bonjour Vanoise,
Merci pour la réponse,

pour l'équation    :



on obtient les équations :





se sont les équations d'un oscillateur harmonique

dans cette force il y a seulement l'état lié pas d'état de diffusion ?
c-à-d on a toujours la trajectoire ellipse et pas hyperbole ou parabole ?

Si k>0 : état lié ; trajectoire elliptique sauf si vitesse initiale colinéaire à vecteur OM : mouvement rectiligne dans ce cas.
Si k<0 : état de diffusion : les solutions des deux équations différentielles font intervenir des exponentielles réelles qui tendent vers l'infini quand t tend vers l'infini.

donc pour l'etat de diffusion on a :

    avec  

qui donne





est ce que la solutions de ces équation différentielle est:

  et  

Nous sommes d'accord !

En fait ta réponse précédente est incomplète. En posant :



Les équations horaires dans le cas le plus général sont :





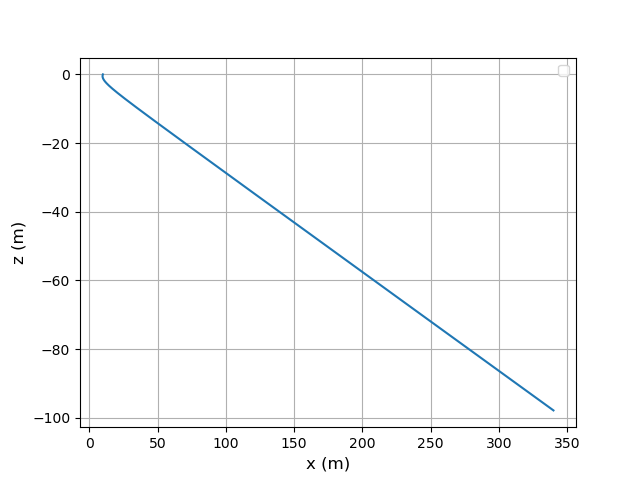
où A,B,C et D sont quatre constantes que l'on détermine à partir des composantes du vecteur position initiale et à partir des composantes du vecteur vitesse initial. A noter que pour   , les exponentielles négatives deviennent négligeables, la trajectoire se confond pratiquement avec son asymptote qui est la droite d'équation :



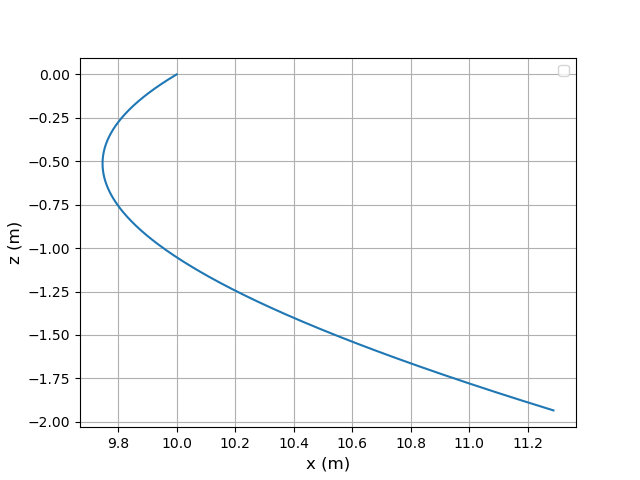
Voir simulation ci-dessous : deuxième courbe : « zoom » sur la trajectoire pour t très faible devant

J'ai choisi pour la simulation : xo=10, zo=0 et un vecteur vitesse initiale tel que v_xo=v_zo valeurs négatives.

Merci Vanoise pour cette explication,
donc si je comprend bien la trajectoire est hyperbole dans un intervalle  puis elle se confondre avec l'asymptote quand t tend vers l'infini.

Je t'ai fourni les équations horaires du mouvement... Qu'est-ce qui te permet d'affirmer que la trajectoire est une hyperbole ?

Bonsoir Vanoise,
Merci pour la remarque,
moi je suppose seulement, mais sans équation, on ne peut affirmer rien

Ton message du  17-03-21 à 21:24 permet de montrer que l'équation différentielle que tu obtiens avec une force en k.r  n'admet pas une solution de la forme :

salut Vanoise,

je trouve dans le référentiel suivant paragraphe II-2 que la trajectoire est une branche d'hyperbole

D'accord.  Je n'avais pas pensé à remplacer les deux exponentielles par des cosinus hyperboliques.  Attention tout de même  : le document traite un cas très particulier. Du coup  : d'accord avec ton message de 11h38

Merci Vanoise,
je trouve dans d'autre référence(des livres) des information qui concerne ce type de force, je veut les partager:

-mouvement à acceleration centrale :



-la vitesse :

   (on utilise la formule :

-l'équation polaire de la trajectoire:

la 1ere formule de Binet:    on pose :   



ce qui donne :

  





les asymptotes :

   et      

-équation cartésienne de trajectoire:



-équation horaire de

la loi des aires :      

ce qui donne



donc :

Merci pour ce document intéressant. Je préfère tout de même la méthode que je t'avais proposé dès le départ , celle qui permet d'obtenir les équations horaires du mouvement, à condition d'y rajouter le complément que tu as proposé hier à 19h19 sur les sinus et cosinus hyperboliques. Mais bon : tout dépend de l'objectif de l'étude ; il est toujours intéressant d'avoir un large choix de méthodes à disposition.

Merci Vanoise.
grâce à vous j'arrive à résoudre les grandes difficultés que je rencontre dans ce sujet.