Inscription / Connexion Nouveau Sujet
force
bonjour,
j'ai un pb suivant :
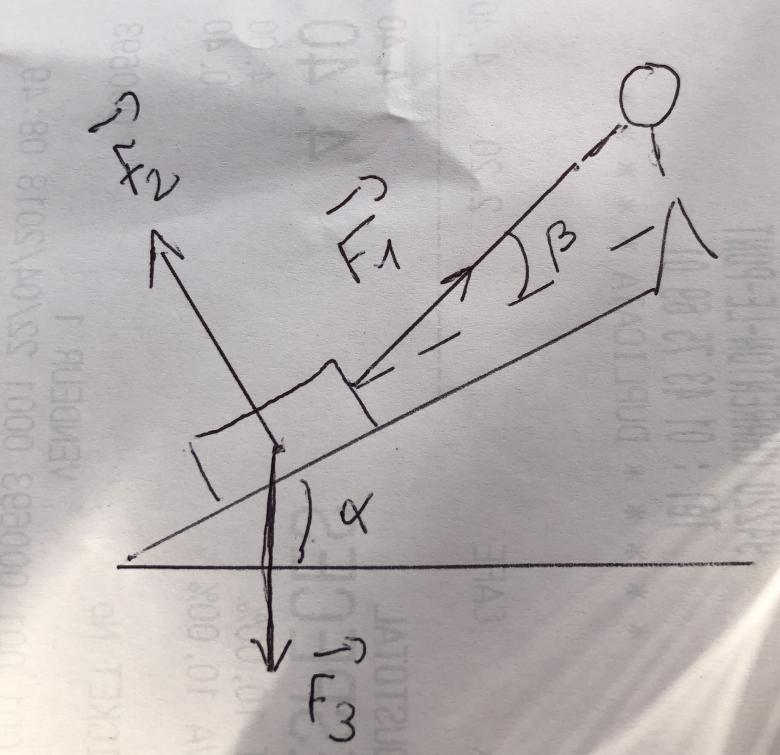
1) quelles sont les actions mecaniques de F1, F2, F3
j'ai dit :
F1 correspond à l'action mécanique exercée par l'esquimau sur le traineau
F2 correspond à l'action mécanique exercée par le sol sur le traineau
F3 correspond à la force gravitationnelle sur le traineau
2)calculer le poids du traineau si m=100kg et g=10N/kg
P = m x g = 100*10 = 1000 N
3)donnez les caractéristiques de F3 :
F3 s'applique sur le traineau, direction : verticale, sens : vers le bas
et la valeur ? je ne vois pas trop .. ou 1000 N ?
4) que peut on dire des forces qui s'exercent sur le traineau?
On peut dire qu'elles s'annulent non? et F1=F2+F3?
Merci
Bonjour,
Je te conseille de relire ton cours car tu as mal assimilé les caractéristiques des forces principales ... D'après ton schéma :
1.
F1 correspond à l'action mécanique exercée par l'esquimau sur le traineau => OK
F2 correspond à l'action mécanique exercée par le sol sur le traineau => c'est faux, il s'agit du poids du traineau
F3 correspond à la force gravitationnelle sur le traineau => c'est également faux, il s'agit de la réaction du support, exercée par le sol sur le traineau. A noter que ton schéma n'est pas correct, la réaction du support n'a pas le centre d'inertie pour point d'application !
2. OK
3. Horreur, comment peux-tu écrire qu'elle est verticale ?!
* Point d'application : point de contact entre le support (= le sol) et le traineau => corrige ton schéma donc ;
* Direction : perpendiculaire au sol ;
* Sens : vers le haut, par rapport à la perpendiculaire au sol ;
* Valeur : F3 (à cette étape, on n'a rien de plus).
4. Je suppose que tu dois avoir un schéma à l'échelle, non ?
Il faut alors faire une construction vectoriel :
* construire la résultante ;
* constater que ;
* donc d'après le principe d'inertie ...
Merci pour la reponse. Alors oui j'ai inversé F2 et F3 sur mon dessin ....!!
Oui il y a une construction à l'echelle à faire avec 1cm=10N
Et alpha=10° et beta=20° Et là c'est un mystere !
Je ne comprends pas votre reponse 4)..
En fait on n'a pas de cours..donc je fais avec ce que je lis
Merci pour l'aide
Salut,
Ton schéma n'est toujours pas correct pour la réaction du support. Relis ce que j'ai écrit sur son point d'application.
Pour la 4, tu as dû voir en maths comment faire une construction vectorielle, non ?

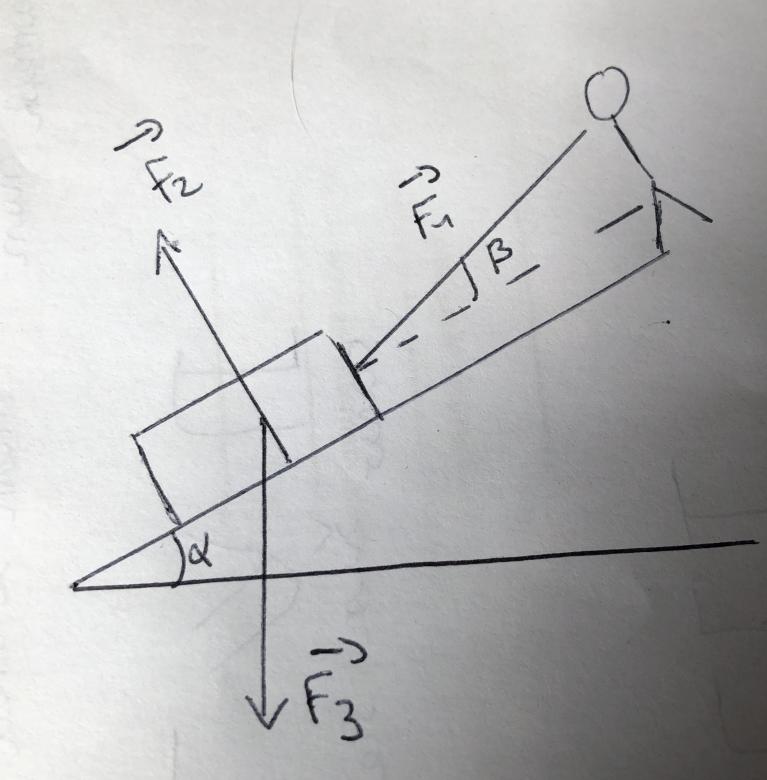
Je reprends avec le nouveau schéma:
1)
F1 =force exercée par l'esquimau sur le traineau
F2 =force gravitationnelle sur le traineau
F3= force exercée par le sol sur le traineau
2) P = m x g = 100*10 = 1000 N OK
3) F3 est une force verticale (direction), orientée vers le bas (sens), qui s'applique au centre de gravité du traineau (point d'application), de valeur 1000N (valeur)
4) que peut on dire des forces qui s'excercent sur le traineau ? je dis que d'apres le principe d'inertie, les forces qui s'exercent sur le traineau se compensent car le mouvement est rectiligne uniforme
5) quelle est la relation entre F1, F2, F3?
F1 = F2 +F3
6) faire un schema à l'echelle avec 1cm = 10N, alpha = 10° et beta =20°
Là je ne vois pas...
merci!
Salut,
1)
F1 =force exercée par l'esquimau sur le traineau
F2 =force gravitationnelle sur le traineau => faux, il s'agit du poids du traineau (on est dans un référentiel terrestre souviens-toi)
F3= force exercée par le sol sur le traineau => c'est la réaction du support exercée par le sol sur le traineau
Attention à bien utiliser le vocabulaire vu en cours
2) P = m x g = 100*10 = 1000 N OK
3) F3 est une force verticale (direction), orientée vers le bas (sens), qui s'applique au centre de gravité du traineau (point d'application), de valeur 1000N (valeur)
Le mieux est de présenter les choses de la façon suivante :
* point d'application : le centre d'inertie G du système, à savoir le traineau ;
* direction (ou droite d'action) : la verticale ;
* sens : vers le bas (ou vers le centre de la Terre) ;
* valeur : F3 = 1000 N
4) OK, j'imagine que c'est précisé dans l'énoncé que tu n'a pas recopié (attention à cela la prochaine fois)
5) Oui, c'est cela en relation vectorielle, encore faut-il le démontrer par une construction vectorielle ...
Soit
Je construis ce vecteur sur le schéma :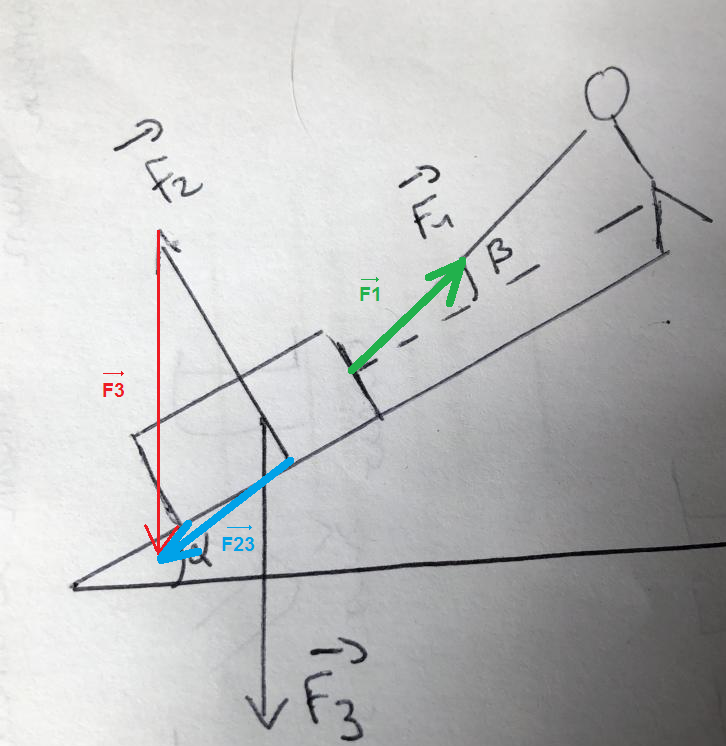
Remarque importante : la contruction vectorielle doit se faire à l'échelle proposée pour que cela marche.
Tu es censé constater que
Les forces se compensent, le principe d'inertie est donc respecté.
Je ne comprends pas tout..car je n'ai pas de cours!
comment trouve t-on F23? pourquoi s'applique t-elle au bas du traineau et non au centre de gravité?
F23 est la resultante de F2 et F3?
et pourquoi on n'a pas F1=F2+F3 ?
pour le dessin à l'echelle je ne vois pas comment faire non plus : si on a F1 = 10 cm (1 cm = 10N dans l'ennoncé) que vaut F2 et F3? 5cm et 5cm?
merci
Tu as des lacunes qu'il va falloir vite combler  :
:
* comment construire le vecteur ?
C'est un point de ton cours de mathématiques, regarde cette vidéo (clique sur la maison) : ![]()
Si ce n'est pas encore clair, le mieux est de se rapprocher de ton professeur de maths et de lui poser des questions.
* Attention : mon schéma n'est pas à l'échelle, c'était pour t'illustrer comment faire une construction vectorielle à partir de deux vecteurs. Regarde la vidéo, tu comprendras mieux.
* Pourquoi on n'a pas ?
Parce que le principe d'inertie ne serait pas respecté :
ce qui est différent de
Pour avoir déjà corrigé cet exercice, il y avait normalement un schéma à l'échelle de fourni.


