Bonjour,

J'ai cherché mais je n'ai trouvé aucune trace de réponse à cet exercice.

Archimède(-287;-212) décrit l'expérience suivante :
"Si tu poses un objet au fond d'un vase et si tu t'éloignes le vase jusqu'à ce que l'objet ne se voit plus, tu le verras réapparaître à cette distance dès que tu le rempliras d'eau"


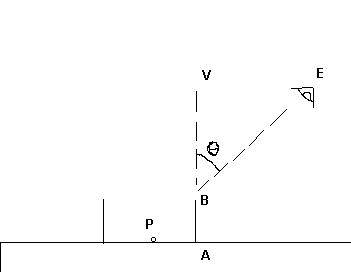
Pour illustrer le principe de cette expérience, on considère un récipient de forme cylindrique, de hauteur égale à 10cm et de diamètre 20cm. On colle au centre du fond du récipient une petite perle P de couleur vive. Le récipient, initialement vide, est posé sur une table horizontale.

La figure est réalisée dans le plan vertical contenant la perle P et la pupille E de l'observateur. On note (V) la droite verticale ayant pour support le côté AB du récpient. On repère la direction d'observation par l'angle thêta que fait le segment[BE] avec (V).

[ j'ai le plus de problème avec cette première question qui est sans doute toute bête]

1.Au-delà de quelle valeur limite thêta_max l'observateur ne verra t-il plus la perle P?

[ je n'ai pas trop compris non plus la suite]
2.a) Construire ce rayon. Quel dioptre rencontre t-il? Quelle est la normale du dioptre ?
je dirai que c'est la séparation au point B bord du récipient et la normale serait donc (v)

voilà les questions qui me posent problème mais une fois résolues je pense pouvoir faire les question suivantes qui sont:

b)Identifier l'angle d'incidence et calculer sa valeur.

c. En déduire l'angle de réfraction

3.Quelle est la nouvelle valeur limite thêta'_max au delà de laquelle l'observateur ne verra plus P dans le récipient rempli d'eau? Archimède avait-il raison?

Merci énormément d'avance pour votre aide!!