Inscription / Connexion Nouveau Sujet
Exercice vanne
bonjour à tous, voila j'ai un exercice à faire pour la rentrée en mecanique des fluides. Voici l'xercice:
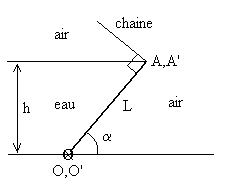
3 – La figure ci-contre représente une vanne rectan-gulaire (L x l) en coupe verticale destinée à fixer le niveau d’eau (hauteur h) d’une retenue. Cette vanne est articulée à sa base sur un axe OO’ et maintenue au sommet par 2 chaînes parallèles manoeuvrées par un treuil. En position haute (angle a) on supposera la direction des chaînes perpendiculaires à la vanne.
1) Calculer la poussée sur la vanne due à la pression hydrostatique et son centre d’application.
2) Calculer les efforts transmis aux chaînes (on négligera le poids propre de la vanne) et la réaction de l’axe OO’.
la figure peut se voir sur ce site:
Donc je l'ai déja commençé:
Il faut partir de la relation dF=-P*DS j'imagine
J'ai d'abord appliqué le PFS entre deux points ce qui donne après calculs p(z)= pa+ ro*g*(h-z)
Après j'a cherché à calculer DS:
donc là je me suis aider avec le triangle et alpha ce qui me donne dS=l*dL or dL=dz/sin
d'ou dS=l* (dz/sin )
)
et après je sais pas quoi faire.. je sais même pas si le début est bon..
Merci de votre future aide et en ésperant que vous aller m'aider =)
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
Déja merci de ta réponse rapide, mais integrer quoi sur z ? et le prof nous a dis aussi qu'il faut faire la même chose pour la partie air...
Je suis un peu perdu la.. meme pour les autres questions je ne vois pas du tout comment faire...
1)
Pression hydrostatique : P(z) = Rho.g.(h-z)
dS = l/sin(a) dz
dF = Rho.g.(h-z) * l/sin(a) dz
dF = Rho.g.l/sin(a). (h-z)dz
F = Rho.g.l/sin(a) S(de 0àh) (h-z)dz (avec S pour le signe intégrale)
F = Rho.g.l/sin(a) . [hz - z²/2](de0àh)
F = Rho.g.l.h²/(2.sin(a))
Et si on remarque que L = h/sin(a) --->
F = Rho.g.l.L.h/2
F = Rho.g.S.h/2 (avec S = L*l l'aire du "panneau" de la vanne).
-----
A quelle hauteur est-elle appliquée ?
A la hauteur H (à partir du fond) telle que :
S(de 0 à h) Rho.g.l/sin(a). (h-z) * (H-z) dz = 0 (somme des moments des dF par rapport au point d'application = 0)
S(de 0 à h) ((h-z) * (H-z)) dz = 0
S(de 0 à h) (hH - hz - Hz + z²) dz = 0
[hHz - (h+H)z²/2 + z³/3](de 0 à h) = 0
h²H - (h+H)h²/2 + h³/3 = 0
H - (h+H)/2 + h/3 = 0
H/2 = h/2 - h/3
H/2 = h/6
H = h/3
-----
La poussée sur la vanne due à la pression hydrostatique est F = Rho.g.S.h/2, elle est normale à la surface de la "paroi" de la vanne et son centre d'application est à une hauteur H = h/3 du fond (au milieu de la largeur l évidemment).
Avec Rho la masse volumique de l'eau, g l'intensité de la pesanteur, S l'aire de la paroie de la vanne et h la hauteur d'eau.
----------
Il ne faut pas tenir compte de la pression atmosphérique car son action est des 2 cotés de la vanne. (en négligeant le poids d'une colonne d'air par rapport au poids d'une colonne d'eau de même hauteur, ce qui est tout à fait légitime).
-----
Sauf distraction. 
ça c'est une réponse =)
Merci beaucoup !
et en fait le centre d'application c'est la hauteur à laquelle elle est appliquée c'est ça ?
Tu es sure de cette correction =)? Moi même en la lisant elle me parait bonne mais je prefère demander =)
Le point d'application est un point, il faut donc plus que une seule cote pour le situer.
Le point d'application se trouve sur la paroi de la vanne, à une distance h/3 du fond et au milieu de la largeur l de la paroi.
Quant à la "justesse" de ma réponse, tout ce que je peux dire est que c'est celle que moi j'aurais faite... Et je l'assume.

Me revoila! donc j'ai bien relis ta correction, j'ai travaillé avec en refaisant l'exercice tout seul, enfin la premiere question et grace a toi j'ai compris =)
Par contre je n'arrive pas la question numéro 2.... a vrai dire notre professeur nous a pas fait cours et nous a donné cet exercice pour les vacances....
donc si on pouvait me re-aider ca serait gentil...
merci de vos futures réponses !
Va lire cet exercice (tout) : ![]() hydrostatique et barrage...
hydrostatique et barrage...
Il est un peu différent, le "mur" est vertical au lieu d'être oblique ... Mais le principe de calcul reste le même.



