Inscription / Connexion Nouveau Sujet
exercice physique lois de snell-descartes
bonjours,
voila j'ai un probleme pour comprendre une question. je ne demande pas la reponce juste une technique pour y arrivé car je suis perdue et ne comprend pas comment faire les calcules pour repondre aux questions voici mon énoncé:
"afin de mesurer l'indice de réfraction d'un liquide, on en verse une quantité suffisante pour emplir un hémicylindre creux, disposé sur un support horizontal. Les parois de ce dernier seront considérées d'épaisseur négligeable.
1°) compléter qualitaivement la marche du rayon lumineux à travers le liquide, puis à la sortie de l'hémicylindre.
2°) calculer la valeur n de l'indice de réfraction du liquide"
Bonjour,
Bienvenue sur l'  pour ton premier problème !
pour ton premier problème !
Un grand principe du forum : avant de poster, faire une recherche pour vérifier que le sujet n'a pas déjà été traité !
Regarde : 
![]()
Pour apprendre à te servir du moteur de recherche : 
![]()
Pour faire ta recherche : 
![]()
Clique sur les maisons, ce sont des liens !

Salut  !
!
1) il nous faudrait la figure, tu vas avoir déviation du rayon au niveau du dioptre plan
2) loi de Snell-Descartes. As-tu des valeurs?
pardon j'ai oublier une ligne (merci de vos réponces)
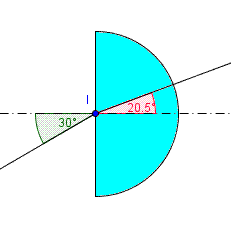
l'hémicylindre est éclairé par de la lumiere monochromique sous un angle d'insidence i=30,0°.
on mesure alors un angle de réfraction r=20,5
et voici le shema qui etait avec bien qu'il n'aide pas beaucoup je trouve
Si, la figure était indispensable, car ou bien le rayon arrive sur le dioptre plan ou bien il arrive sur la partie cylindrique.
Que dis-tu "qualitativement" du trajet du rayon arrivant au centre du cylindre mais sur un dioptre plan ?

Il change de direction.
Comme il entre dans un milieu dont l'indice est supérieur à celui de l'air il va se rapprocher de la normale au dioptre.
Il devient alors un rayon dans l'hémicylindre.
Que se passe-t-il à la sortie de l'hémicylindre ?

il change de direction et de coté de la normal l'angle entrele rayon et la normal n'est plus le meme (puisque il devien l'angle rétracté)
Oui, l'angle refracté a une mesure plus faible que l'angle d'incidence (regarde les valeurs de ton énoncé :
angle d'incidence : 30°
angle réfracté : 20,5°)
Que devient le rayon à la sortie de l'hémicylindre ? Quelle y est son angle d'incidence ? Et donc que vaut son angle de réfraction à la sortie ?

le rayon diminu
je pence en revenche les deu autres question je ne pourai pas te répondre c'est la que je bloque 
le probleme c'est que je ne sas pas comment faire
mais pourquoi je doit calculé l'indice du liquide qui remplit l'hémicylindre?
oui j'ai été voir mais malheureusement je ne comprend pas en cours et mon cours est pas plus explicite j'ai été voir le lien qu tu ma donner avent de crée ce topic mais je ne comprend pas la loi qui dit sin i = sin r * k
Pour prendre les mêmes notations que ton énoncé, nous écrirons :
sin(i) = n  sin(r)
sin(r)
L'angle d'incidence vaut i = 30°
l'angle de réfraction vaut r = 20,5°
Tu en déduis facilement la valeur de n (en utilisant ta calculatrice, évidemment).

K c'est le rapport de l'indice de réfraction du liquide, n, à l'indice de l'air qui vaut 1
K = n / 1 = n

alors voila ce que j'ai trouvé
sin i= 0,5
sin r = 0,35
soit indice de réfraction = sin i = sin R * N
donc n = 0,5 - 0,35 = 0,15
c'est correcte ? 
Allez je me permets de revenir après la bataille 
Si tu as un angle d'incidence de 90°, le rayon incident rase la surface du liquide, l'angle de réfraction atteint sa valeur maximum : c'est l'angle limite de réfraction.
Si tu veux approfondir :
Sachant que sin(90) = 1, en remplaçant dans la formule de Snell-Descartes, on peut déterminer la valeur de l'angle limite :
sin(i)/sin(r) = n <=> sin(r) = sin(i)/n
Si tu as de l'eau, liquide pour lequel n = 1,33333... = 4/3, tu as donc n = 4/3 <=> sin(r)= 3/4 => r = 48°
Si l'incidence est plus importante que 48°, le rayon ne quitte plus le liquide et reste dans l'eau en étant réfléchi sur la surface de l'eau comme sur un miroir : on assiste à une réflexion totale (mais il faut pour visualiser ceci que le rayon lumineux passe d'un milieu plus réfringent vers un milieu moins réfringent et que l'angle d'incidence soit plus grand que l'angle limite de réfraction).

 !
!