Inscription / Connexion Nouveau Sujet
Exercice:Equilibre d'un solide soumis à l'action de 3 forces
Bonsoir,
J'ai besoin d'aide s'ils vous plait,
je n'arrive pas à traiter les questions demandés s'ils vs plait un coup de main.Merci d'avance
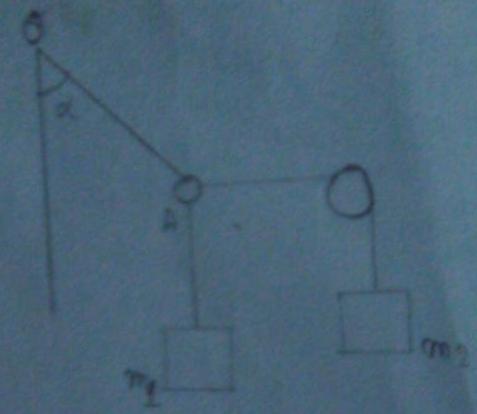
Exercice:les masses des fils et de l'anneau sont negligeables.
A l'equilibre,le fil OA fait un angle de 
=45° avec la verticale
1)Calculer la masse m2 pour realiser cet equilibre .
2)Calculer la tension du fil OA.
3)Cet equilibre depend t-il de la valeur de g?
Donner:p1=4N; g=10N/kg
Bonsoir,
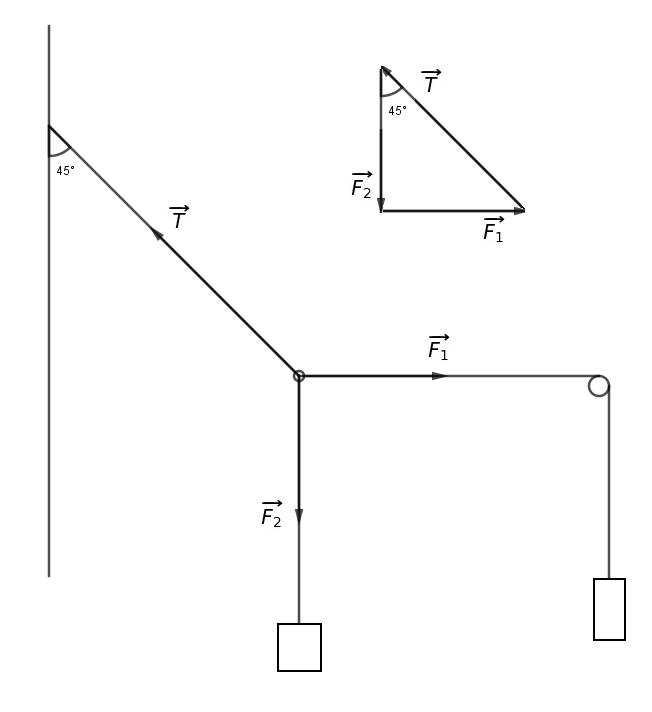
On étudie l'équilibre de l'anneau A :
Celui-ci est soumis à l'action de trois forces :
a) Une force verticale, dirigée vers le bas dont l'intensité est égale au poids P1 = 4N
b) Une force horizontale, dirigée vers la droite dont l'intensité est égale au poids P2 lui-même égal à m2*g
c) Une force oblique formant un angle de 45° avec l'horizontale.
Il faut à partir de A représenter chacune des trois forces par un vecteur, de manière que la somme de ces trois vecteurs soit égale au vecteur nul.
La figure formée par ces trois vecteurs est très simple et elle permet à partir de règles de géométrie bien connues de répondre aux questions posées.
Oui, c'est exact.
Tu dois pouvoir maintenant répondre facilement aux questions posées en utilisant une technique géométrique de ton choix.
Voila comment j'ai procedé:
Par projection sur les axes nous avons:
0-Tx+F=0=>F=Tx=> F=T.sin
-p1+Ty+0=0 => Ty=p1 => p1=t.cos.
Utilisons le rapport F sur P
F/P=tan => F=p.tan or F=p2=m2g. ==>m2g=p.tan => m2=p.tan/g
AN m2=4N×tan45°/10N/kg=0,4 kg
Oui, ton résultat est exact.
Il te reste à calculer la valeur de la tension du fil OA
Remarque :
La technique de la projection sur les axes est très efficace, elle fonctionne dans tous les cas.
Toutefois lorsque la figure vectorielle est particulièrement simple (ici, les trois vecteurs forment un triangle rectangle qui va s'avérer isocèle à cause de l'angle de 45°) cette technique peut apparaître un peu "lourdingue".
C'est pour cette raison que j'avais représenté les vecteurs en dehors du schéma principal car on voit alors que :
tan(45°) = F1/F2 donc F1=F2 puisque tan(45°) = 1
Or F1=P1 = 4N donc F2=F1=4N
m2 = F2/g = 4/10=0,4kg
Et T² = F1²+F2² = 4²+4² = 32
T = 
32 = 5,6N
Ok j'ai compris.Merci.
donc Pour T .
Par projection sur l'axe des y'y on a:
P=T.cos
=>T=P/cos
AN)T=4N/cos45°=5,65 N
T=5,6N.
S'ils vous plait je n'ai pas compris la 3éme question pouvez vous m'expliquer d'avantage
Une fois l'équilibre réalisé, supposons que " g " varie.
Que va t'il se produire ?
Les valeurs des poids accrochés aux fils vont changer, mais comme ces valeurs étaient égales entre elles, elles le resteront.
Les intensités des forces F1 et F2 qui sont égales aux poids vont changer, mais on aura toujours
F1 = F2 et tan() = F1/F2 = 1 ne changera pas donc le fil restera incliné à 45°
F1 et F2 ayant changés, la valeur de aura changé aussi.
Finalement, l'équilibre restera le même, mais la tension des différents fils aura varié.
Annuler
connectez vous