je trouve ir2 = 19.9°

Je me trompe ?

Bonjour,

Je trouve plutôt 19,3°

Oui, merci, je viens de m'apercevoir de mon erreur : J'ai oublié les sinus...

Pour une question suivante :

Déterminer la valeur de l'angle d'incidence i'r1 lorsque le faisceau rouge va sortir du prisme


Euh oui... comment je peux faire ça ?

Avec un théorème de géométrie (c'est de l'optique géométrique ! )
N'oublie pas que l'angle au sommet du prisme vaut 60°

Figure obligatoire ! (Comme toujours en géométrie et donc en optique géométrique).

Mais.. C'est de la physique ! Pas de la géométrie ...

Et j'ai peut-être trouvé quelque chose...
Tu peux me dire ce que tu en pense ?

ir2 = i'r1 car les deux normales sont parallèles donc la droite qui coupe ces deux parallèles forment le même angle
donc i'r2 = 19.3°

Dans une autre question, on me demande de calculer l'angle i'r2 du rayon rouge à sa sortie du prisme.

Je trouve :

sini'r2 = (sini'r1 x n.rouge) / n.air = 0.5
Donc i'r2 = 30°

C'est ça ou... ?

Les normales seraient parallèles si le rayon traversait une lame à face parallèle (par exemple une vitre).
Mais il traverse un prisme d'angle au sommet 60°
___________

Dans la boîte à outils du physicien il y a tout ce que les mathématiciens lui ont préparé. Entre autres la géométrie...

Je peux vous donner le sujet ?

En gros :


Un faisceau de lumière blanche arrive sur un prisme en verre d'indices de réfraction
n.rouge = 1.51 et n.bleu = 1.55
L'angle au sommet du prisme est 60°
L'angle d'incidence du faisceau avec la normale à la surface du prisme est de 30°

Questions :

1) On s'intéresse à la composante rouge du faisceau lumineux.Déterminer la valeur de l'angle de réfraction ir2 dans le prisme.

2) Déterminer la valeur de l'angle d'incidence i'r1 lorsque le faisceau rouge va sortir du prisme.

3) Calculer l'angle i'r2 du rayon rouge à sa sortie du prisme.

4) On s'intéresse maintenant à la composante bleue du faisceau lumineux. Déterminer la valeur de l'angle de réfraction ib2 dans le prisme.

5) Déterminer la valeur de l'angle d'incidence i'b1 lorsque le faisceau rouge va sortir du prisme.

6) Calculer l'angle i'r2 du rayon rouge. Que peut-on en conclure ?

Rhô... je bloque trop sur la question 2) ... Quelqu'un n'aurait pas un tuyau ? Je suis au même point depuis une demie heure... =/

Rhô s'il vous plait je n'y arrive pas toute seule...

Je ne vois pas ce que ça m'apporte de savoir que ce prisme a un angle de 60° ...

Abyssluciole, si tu fais un schéma de la situation tu verras tout de suite ce que ça t'apporte

J'ai fait un schéma.. Mais je ne vois rien

S'il vous plait

Aaah je crois avoir enfin trouvé !
Dans un triangle, la somme des angles fait 180°

Donc, le sommet du prisme fait 60°
Ensuite on fait 180 - (70.7+60) = 49.3
90 - 49.3 = 40.7

Donc, d'après moi, cet angle d'incidence i'r1 mesurerait 40.7°

C'est juste ?

Non ça doit pas être ça.. puisqu'après je trouve i'r2 = 90° ...

Je vous en pris, je sèche totalement

Eh bien voilà !

Oui, c'est cela ; mais fais attention à ne pas arrondir les valeurs trop violemment sinon tu ne vas plus rien comprendre de cet exercice.

A l'entrée du prisme : i₁ = 30°
indice de l'air, quelle que soit la couleur n_air = 1
pour le rayon rouge, indice du prisme n_rouge = 1,51

angle de réfraction à l'entrée r_1.rouge
n_air.sin(i₁) = n_rouge.sin(r_1.rouge)

et donc
sin(r_1.rouge) = (n_air / n_rouge).sin(i₁)
d'où
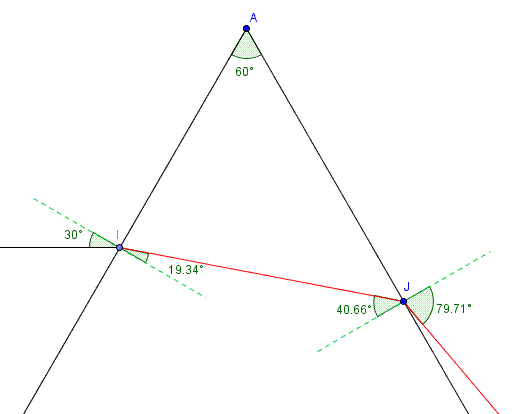
r_1.rouge 19,337°
_____________

Quand l'angle de réfraction à l'entrée vaut r₁, que vaut l'angle d'incidence à la sortie i₂ ?

La somme des angles d'un triangle vaut 180°
L'angle au sommet du prisme est A = 60°

(90 - r₁) + A + (90 - i₂) = 180°
donc
A - r₁ - i₂ = 0
ou
i₂ = A - r₁
_____________

Puisque r_1.rouge 19,337°
alors
i_2.rouge 60 - 19,337 40,663°

Angle de réfraction à la sortie :

n_rouge.sin(i_2.rouge) = n_air.sin(r_2.rouge)

sin(r_2.rouge) = (n_rouge / n_air).sin(i_2.rouge)
d'où
r_2.rouge 79,7°

Il te reste à faire le même travail pour le rayon bleu.
_____________

Note : il peut arriver, on ne sait jamais... , que l'on ne puisse pas calculer l'angle, parce qu'un sinus ne peut pas être supérieur à 1
Mais ton cours t'explique que parfois il y a réflexion totale...

A suivre !

Avec une figure (indispensable, mais parfois un peu longue à faire exactement) :