Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. SecondeForum de secondes PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau seconde
Partager :

Exercice difficile en physique

Posté par
Sarouche 10-05-12 à 20:11

Bonjour
Voila j'ai trouvé l'exercice suivant :
Pour calculer la masse de la Terre Mt et son rayon Rt , nous  avons fait les deux experiences suivante
La premiere Sur la terre :  nous avons calculer le poid d'un corps dont sa masse est de 10 Kg son poid etait de 68N
La deuxieme Dans un vaisseau spatial qui s'eleve a 3600 KM de la terre, nous avons calculé le poid du meme corps le resultat etait de 40 N
Calculez le rayon Rt et la masse terrestre   Mt

Mes essais
J'ai d'abord calculer la gravité
Sur terre :
P=mg   => g0 = P/m = 6.8N/kg
Dans l'espace  => g= p/m = 4N /kg
Puis j'ai pensé a utlisé l'intiative suivante
G0/g = Rt2 / (Rt+h)2
Je sens que c'est faux :/ pouvez vous m'orientez svp ?

Posté par
bibere : Exercice difficile en physique 10-05-12 à 21:01

Bonjour,

Oui tu as quasiment raison pour la formule à utiliser. On va utiliser la relation liant la masse de la Terre, la masse du corps et la distance séparant les centres de gravités de la Terre et de l'objet.

F_{Terre}=G\times\frac{M_T\times m}{R_T^2}      ça c'est pour le poids sur Terre

F_{espace}=G\times \frac{M_T\times m}{(R_T+h)^2}    ça c'est pour le poids dans l'espace

On a donc un système de deux équations à deux inconnues, on connait m, G et h, choisis la méthode que tu veux pour résoudre ce genre de système, tu peux remplacer une des inconnues dans la seconde équation et résoudre la seconde équation ensuite tu remplaceras ce résultat dans l'équation de la première relation.

Posté par
Sarouchere : Exercice difficile en physique 10-05-12 à 22:15

Merci d'avoir repondu
Donc si j'ai bien compris
Sur Terre :
g0 = GM/R2
6.8=(6.67*10-11 MT)/ R2
Mt/ R 2 = 6.8/6*10-11
Apres je fais pareil pour
g=G M / ( R+h) 2  ????
Ou alors
g0/g = Rt2 / (Rt+h)2
Je remplace et j'obtiens Rt
Puis avec
g0 = G * MT / Rt 2  J'obtiens la masse ?

C'est qui qui est la plus correcte s'il vous plait

Posté par
Sarouchere : Exercice difficile en physique 10-05-12 à 22:17

Pardon pour le premier poids sur la terre c'est 96 N ce qui nous donne une gravité de 9.8 N/KG (sur Terre)

Posté par
bibere : Exercice difficile en physique 10-05-12 à 22:44

Par la suite, chaque bloc de 2 équations est en réalité un système de deux équations mais comme je n'ai pas regardé comment mettre des accolades autour j'ai un peu séparé chaque bloc.

G\times \frac{M_T\times m}{R_T^2}=96
G\times \frac{M_T\times m}{(R_T+h)^2}=40


M_T=\frac{96\times R_T^2}{m\times G}
(R_T+h)^2=G\times \frac{M_T\times m}{40}


M_T=\frac{96\times R_T^2}{m\times G}
R_T^2+2R_T.h+h^2=G\times \frac{96\times R_T^2\times m}{m\times G\times 40}


M_T=\frac{68\times R_T^2}{m\times G}
R_T^2+2.R_T.h+h^2=2,4.R_T^2


M_T=\frac{68\times R_T^2}{m\times G}        (1)
-1,4.R_T^2+2.R_T.h + h^2=0        (2)

Dans (2), on résout l'équation du second degré en calculant le discriminant:

\Delta =(2.h)^2-4\times (-1,4)\times h^2
\Delta =4.h^2 +5,6.h^2=9,6.h^2

\Delta >0   on a donc deux solutions réelles distinctes:

R_{T1}=\frac{-2.h + \sqrt{9,6.h^2}}{2\times (-1,4)}

R_{T_2}=\frac{-2.h - \sqrt{9,6.h^2}}{2\times (-1,4)}=6 555 km             Attention: Quand on fait les calculs, on doit mettre les grandeurs dans les unités du système international donc les distances en m, les masses en kg et les poids en N. J'ai cependant donné le résultat en km mais quand tu fais le calcul le résultat en donné en m.

Seule la solution RT2 donne un rayon RT>0 (une distance ne peut pas être négative sauf si on précise que c'est une longueur algébrique mais ça n'est pas le cas). Donc on a trouvé le rayon de la Terre qui si tu fais le calcul et que tu le compares au rayon équatorial de la Terre, tu verras qu'il n'y a pas une "grande" différence.

Je pense que tu es assez grand(e) pour pouvoir remplacer RT dans l'expression de MT pour avoir la masse de la Terre. Je ne sais pas si ta méthode était fausse ou non mais je trouve que celle-ci, bien que plus compliquée, est la plus sûre pour ne pas se tromper (en étant un minimum rigoureux). Fais comme tu pensais le faire et vérifies tes résultats avec ceux ci pour voir si tu trouves la même chose ou non?

Posté par
Sarouchere : Exercice difficile en physique 10-05-12 à 23:12

OK merci je vais m'y mettre dé demain matin la je suis crevée
Merci encore, j'espere vous trouvez demain en cas de question
Bonne soirée ^^

Posté par
bibere : Exercice difficile en physique 10-05-12 à 23:14

Ok. Si il y a une (ou plusieurs) étape(s) que tu n'as pas compris, n'hésite pas à le dire. Si je ne répondais pas demain, il y a encore le week end...

Bonne soirée.

Posté par
Sarouchere : Exercice difficile en physique 10-05-12 à 23:24

Pour etre franche je n'ai pas bien compris cette etape
Le debut est clair mais apres pourquoi avoir ajouter 96 et 40 ( le poid) ?
Je dois etre fatiguée x(
Merci encore .... et pardon du derangement

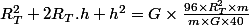
Exercice difficile en physique

Posté par
Sarouchere : Exercice difficile en physique 11-05-12 à 13:02

Bonjour
J'ai essayé de résoudre avec ma formule du debut ce qui m'a donné
Rt = 6463 KM  
Pour la masse
J'ai utilisé
Mt = ( g0 * R2  )/ G = 6*10^24

Je pense que c'est O.K

Posté par
bibere : Exercice difficile en physique 11-05-12 à 17:49

Si tu trouves la même chose c'est bon. Si tu vérifies sur Wikipedia tu trouveras les mêmes valeurs que tu as trouvées.

Posté par
Sarouchere : Exercice difficile en physique 11-05-12 à 21:49

C'est ce que j'ai fait xD
Merci encore pour votre aide ^^ bonne soirée  


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !