Étude d’un circuit avec condensateurs et résistance : exercice de sciences physiques de autre - 275768

1 2 +
 Posté par 
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance  01-05-15 à 08:57
Merci

Mais je n'arrive pas à trouver une primitive... Et pourquoi n'y a-t-il pas d'exponentiel dans le résultat final?
 Posté par 
gggg1234re : Étude d’un circuit avec condensateurs et résistance  01-05-15 à 09:39
Aux constantes pres, 

I^2 est de la forme e(-at)^2

Qui vaut e(-2at)

Qui s'integre en e(-2at)/ (-2a)

Fais ca avec i(t) et en prenant toutes les constantes correctement
 Posté par 
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance  01-05-15 à 10:21
Ca me donne :

C'est ca?
 Posté par 
J-Pre : Étude d’un circuit avec condensateurs et résistance  01-05-15 à 10:49
Citation :
C'est ca?

Presque.

Le  ne devrait pas être là.

Il faut ensuite calculer la valeurs de l'intégrale compte tenu des bornes d'intégration (de 0 à +oo)...

Et penser que pour avoir l'énergie dissipée dans R, il restera encore à multiplier par R. 

 Posté par 
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance  01-05-15 à 12:03
D'accord, merci 

On a vu en cours que quand on a une intégrale en , il faut faire la limite, or ici on a que en , ça tend vers ... 
 Posté par 
gggg1234re : Étude d’un circuit avec condensateurs et résistance  01-05-15 à 14:01
Non en +inf, il y a un "moins" devant le t donc l'expo,nentielle tend vers 0
 Posté par 
J-Pre : Étude d’un circuit avec condensateurs et résistance  01-05-15 à 14:46
Attention MissMlleMoi,

Tu as beaucoup de lacunes ...

Il va falloir sérieusement travailler pour essayer de les combler.

 Posté par 
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance  01-05-15 à 14:48
Ah oui merci! J'avais oublié ce petit signe... 

J'ai bien trouvé le même résultat de  du coup 

Pour la suite, je ne vois pas comment est ce qu'on peut calculer  de  si on a aucune valeurs?
 Posté par 
J-Pre : Étude d’un circuit avec condensateurs et résistance  01-05-15 à 14:57
On ne te demande pas une valeur numérique de EJ de R ...

Il suffit d'exprimer EJ de R en fonction de ce qui est donné en littéral (soit en fonction des symboles Qo, C1 , C2 ... et R (qui devrait être absent de la réponse)).

 Posté par 
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance  01-05-15 à 15:03
C'est ce qu'on a calculé précédemment non?
 Posté par 
J-Pre : Étude d’un circuit avec condensateurs et résistance  01-05-15 à 17:46
Oui, là où tu as écris : 
Citation :
J'ai bien trouvé le même résultat de J-P du coup.

 Posté par 
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance  01-05-15 à 17:56
Donc la  et la  sont les mêmes questions?
 Posté par 
J-Pre : Étude d’un circuit avec condensateurs et résistance  01-05-15 à 19:45
Je pense qu'on demande de calculer EJ de 2 manières différentes.

La 2eme méthode (qui est, je pense, la réponse à la question 7) pourrait être :

Energie initiale : E1 = 1/2. C1.U1(0)² = (1/2) * C1 . Qo²/C1² = Qo²/(2.C1)

Energie capacitive pour t --> +oo : E2 = 1/2 C1.((U1)oo)² + 1/2 C2.((U2)oo)² = (1/2).(C1+C2) * [Qo/(C1+C2)]² = Qo²/(2(C1+C2))

On a : Ec1 = Ec2 + EJ

Qo²/(2.C1) = Qo²/(2(C1+C2)) + EJ

EJ = Qo²/2 * (1/C1 - 1/(C1+C2))

EJ = Qo²/2 * (C1+C2-C1)/(C1(C1+C2))

EJ = Qo²/2 * C2/(C1(C1+C2))

EJ = Qo².C2/(2.C1.(C1+C2))

Même réponse (heureusement) que par le calcul de S(de0à+oo) R.i² dt fait dans les réponses précédentes (et qui est la réponse à la question 8)

 Posté par 
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance  02-05-15 à 09:11
Ah oui d'accord... Merci 

Pour la , on a :

Pour la , on sait que  donc  et 

Apès je pense qu'il faut utiliser les relations de la question , mais je ne sais pas comment faire...

Pour la , j'avais posé 

Mais là du coup, est ce qu'on peut tout simplement poser ?

 Posté par 
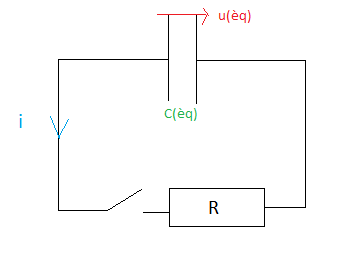
gggg1234re : Étude d’un circuit avec condensateurs et résistance  02-05-15 à 11:12
Oui tau= r Ceq

Attention pour la 11 je crois que c'est tau= r c1c2/(c1+c2)

C'était déjà le Ceq sans qu'on l'utilise directement

Pour les equations une fois simplifie le systeme ets tres facile

Maille:

Ueq +ri=o

On remplace i par Ceq dUeq/dt

Et tu obtiens une equation diff de premier ordre tre ssimple a resoudre 

Ueq=a e(- tau/t)

Etc...
 Posté par 
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance  02-05-15 à 12:02
D'accord merci 

Pour la , est ce que je dois utiliser les réponses de la question ?
 Posté par 
gggg1234re : Étude d’un circuit avec condensateurs et résistance  02-05-15 à 14:19
Oui 2 et 3 peuvent te servir
 Posté par 
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance  02-05-15 à 15:41
Du coup pour la , on a  car 
  Posté par 
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance  02-05-15 à 18:11
C'est ca