Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... AutreForum autre de supérieur PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie

1 2 +

Niveau autre
Partager :

Étude d’un circuit avec condensateurs et résistance

Posté par
MissMlleMoi 23-04-15 à 14:58

Bonjour à tous! J'ai un exercice assez long d'électricité, et j'ai beaucoup de mal à le faire...
Merci d'avance à ceux qui pourront m'aider!


Énoncé:

On considère un circuit formé d'une seule maille contenant deux condensateurs de capacité C_1 et C_2 en série avec une résistance R et d'un interrupteur.
Pour tout t < 0, on considère que l'interrupteur est ouvert.
Pour tout t < 0, le condensateur 1 est chargé d'une charge Q_0 > 0 et l'autre est decharge.
À t = 0 on ferme l'interrupteur. On note i l'intensité du courant circulant dans la maille, u_1 et u_2 les tensions aux bornes des condensateurs 1 et 2.
On traitera les questions sans simplifier le circuit.

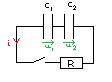
1) Faire un schéma représentant le circuit et précisant les conventions électriques adoptées.

2) Donner l'expression de u_1(0-), u_1(0+), u_2(0-), u_2(0+), i(0-), i(0+).

3) Comment vont se comporter les condensateurs en t -> +\infty? En déduire une relation entre u_1(+\infty) et u_2(+\infty). En déduire une relation entre les charges q_1(+\infty) et q_2(+\infty) portées par les condensateurs en régime permanent.

4) Établir une relation entre les charges q_1(t) et q_2(t) portées par les condensateurs. En déduire une relation entre u_1 et u_2 à tout instant t > 0.

5) Établir l'équation différentielle satisfaite par u_1 pour tout t > 0. Donner l'expression de la constante de temps \tau du circuit. Résoudre l'équation différentielle satisfaite par u_1. En déduire u_2 et i. Tracer u_1, u_2 et i sur le meme graphe en fonction du temps.

6) Calculer la variation d'energie \Delta E1 et \Delta E2 des condensateurs 1 et 2 entre t = 0 et t -> \infty. Que peut-on dire de leurs signes?

7) On note EJ l'énergie dissipée par effet Joule dans la résistance entre t = 0 et t -> \infty. Effectuer un bilan energetique dans le circuit. En déduire une expression de EJ

8) Calculer directement l'énergie EJ dissipée par effet Joule dans la resistance. On souhaite maintenant retrouver une partie des résultats précédents en simplifiant le circuit.

9) Quelle est la capacité C du condensateur équivalent aux condensateurs 1 et 2? Dessiner le schéma du circuit équivalent.

10) Quelle est la charge initiale q_0 = q(0) et la charge finale q(+\infty) portée par le condensateur équivalent?

11) Exprimer \tau en fonction de R et C. Donner l'expression de la tension u(t) aux bornes du condensateur équivalent, de sa charge q(t) et l'intensité i(t). Exprimer la variation d'energie \Delta E du condensateur équivalent entre t = 0 et t -> +\infty et en déduire l'énergie EJ dissipée par effet Joule dans la meme période. Comparer aux résultats précédemment obtenus.


Ce que j'ai fais:
1) Voir l'image plus bas.

2) Ça j'ai réussi.

3) C'est à partir de là que je bloque... Je trouve que que u(+ \infty)=E à l'aide de la loi des mailles, et que donc les condensateurs vont se comporter comme des circuits ouverts.
u(+ \infty)=u_1(+\infty)+u_2(+\infty) or q(+\infty)=Cu(+\infty)=C[u_1(+\infty)+u_2(+\infty)]=Cu_1(+\infty)+Cu_2(+\infty)
donc q(+\infty)=q_1(+\infty)+q_2(+\infty)
Mais là je viens de remarquer que c'est faux car q_1(+\infty)=C_1 u_1(+\infty), de même pour q_2(+\infty)...

Pour la suite, je bloque aussi.

Encore merci pour votre aide!

Étude d’un circuit avec condensateurs et résistance

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 23-04-15 à 15:50

pour moi tu as u1(inf)+u2(inf)=E

et donc q1(inf)/C1 + q2(inf)/C2=E

attebtion dans tes calculs tu utiles C (sans distinguer C1 et C2) ca e parait dangeruexc)

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 23-04-15 à 15:53

lol! je me laisse avoir par tes réponses!

Pour moi E=0

et donc

u1(inf)+u2(inf)=0

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 24-04-15 à 08:15

Pourquoi E=0?

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 24-04-15 à 09:52

Ben, à l'inverse, dis moi à quoi correspondrait ton E?

il n'y a pas de générateur dans le circuit.

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 24-04-15 à 09:54

sauf si tu appelles E=Ri ?? mais c'est pas hyper logique

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 24-04-15 à 16:49

En réalité, j'avais appliqué la loi des mailles sans réfléchir  

Donc pour la question 3) on a: \dfrac{q_1(+\infty)}{C_1} + \dfrac{q_2(+\infty)}{C_2} =0

Et donc pour la 4) on peut écrire \dfrac{q_1(t)}{C_1} = - \dfrac{q_2(t)}{C_2} Tout simplement? ou bien il faut que je trouve une relation sans utiliser C_1 et C_2?

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 24-04-15 à 16:56

non c'est bien C1 et C2 sont des constantes du pb..

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 24-04-15 à 16:57

mais tu es sure que Q0 n'intervient pas?

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 24-04-15 à 17:00

en gros, il faut comprendre le pb, tu as un des condesateur qui est chargé ua debut, l'autre qui st vide.
T donc ca va osciller, le premioer va charger le second, et inversement..jusqu'a que ca se stabilise.

donc je dirais plutot q1(t)+q2(t)=Q0 non?

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 25-04-15 à 13:36

Pour la 4), on cherche la relation entre q_1 et q_2 pour t>0, or Q_0>0 c'est pour t<0... Ça n'a pas d'importance?

Si on considère que q_1(t)+q_2(t)=Q_0 alors C_1u_1(t)+C_2u_2(t)=Q_0

J'ai du mal à me rendre compte de ce qu'est Q_0 en fait...

Posté par
gggg1234T 25-04-15 à 15:33

J'essaie de t'expliquer ce qu'est un condensateur:

C'est un composant un peu comme un "reservoir".
Il se charge qd il y a une surtension et il se decharge qd il y a une baisse de tension.

Et donc qd tu as deux condensateur dans un circuit a vide, en gros l'un va remplir l'autre puis l'inverse etc etc....

Qo c'est la charge à t=o du premier. (Ou t<o c'est un peu pareil, c'est pour dire que c'est une condition initiale du systeme)

C'est un peu comme si tu avais deux seaux. Et on te dit que a t= o le prmier seau contient 10 lites et l'autre est vide.

Ensuite pour comprendre comme se passe ce "tra,sfert" ben ce sont tes equation qui te le disent
Et notamment i=dq/dt= c du/dt qui correspond. Ce que je te dis: su u augmente, la charge augmente, et si u diminue, la charge diminue...'

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 29-04-15 à 16:16

Merci, j'ai compris le fonctionnement maintenant

Mais est-ce que je peux quand même utiliser la loi des mailles?
Car pour la question 2), pour déterminer i(0^+), je l'utilise:

E=u(0^+)+Ri(0^+) => i(0^+)=\dfrac{E}{R} car u(0^+)=0 et donc i(0^+)=0 car E=0

C'est bien ça?

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 29-04-15 à 16:55

oui mais encore une fois, je ne vois pas pourquoi tu fait apparaitre un E

La loi des maille te donne direct u+Ri = 0
(Elle te donne u +Ri=E qd il y a un generateur dans le circuit, mais ici, non tu peux écrire directement E=0 sans meme le mentionner)

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 29-04-15 à 17:31

3) u1(+inf)+u2(+inf)=0
q1(+inf)/C1+q2(+inf)/C2=0

4)q1+q2=Qo
C1u1+C2u2=Qo

5)maille
u1-u2+Ri=0
u1+(-Qo+C1u1)/C2+RC1du1/dt=0
u1 (1+C1/C2) + RC1 du1/dt = Q0/C2
u1 (C2+C1/RC1C2) +  du1/dt = Q0/RC2C1

que tu dois resoudre (equation à verifier)
c'est du classique ca se resout (soltuion sans second membre, en u1=Ae(-tW) ou W va valoir RC1C2/(C1+C2)  (qui est d'ailleurs le "C" equivalent)

a resoudre avec les conditions initiales du second membre pour trouver le A

connaissant u1, tu trouve u2 puis i facilement

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 29-04-15 à 17:31

pardon c'est e(-t/W)

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 29-04-15 à 17:33

Ah d'accord! Merci

Pour la 3), quand t->+\infty, un équilibre s'établit entre la charge et décharge de chaque condensateur donc on a :

i(+\infty)=0 donc u(+\infty)=u_1(+\infty)+u_2(+\infty)=0

Pour la 4), comme q_1(t)+q_2(t)=Q_0, on a que C_1u_1(t)+C_2u_2(t)=Q_0

Est ce qu'on peut considérer que C_1=C_2=C?

Pour la 5), l'équation différentielle vérifiée par u_1 est: \dfrac{du_1}{dt}+\dfrac{u_1}{RC_1}=0
On peut poser \tau=RC_1. Donc u_1(t)=\alpha e^{\dfrac{-t}{\tau}}, avec \alpha un réel.
Pour déterminer \alpha, on utilise les conditions initiales : comme u(0+)=0, \alpha e^{0}=0 donc \alpha=0...

Mais du coup ca me donnc u_1(t)=0... C'est normal?

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 29-04-15 à 17:40

4) non C1 et C sont donnés, ils sont différents.

5) non, regarde ma reponse précédente

tu pars des mailles:
u1-u2+Ri=0

tu sais que i=C1du1/dt  (ou C2du2/dt, mais on veut calcule ru1 nous)
donc
u1-u2+RC1du1/dt=0

ensuite on remplace u2 par (Qo-C1u1)/C2  (qui vient du 4)

et donc

u1-(O0-C1u1)/C2 +RC1 du1/dt=0

et on simplifie tout ca

u1 (C2+C1)/C2 + Rc1 du1/dt = Qo/ C2

on simplide encore


u1 (C2+C1)/Rc1C2 + du1/dt = Qo/ Rc1C2

qui est une equation diff de degré 1 avec second memebre.

Ton taux c'est RC avec C=C1C/(c1+c2) tu reconnais la constante equivlente à deux condesateur en serie !! come par harsard

la soltuoon est bine u1=Ae(-t/taux)
et tu rtouves A avec le second membre..

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 29-04-15 à 18:36

Ah oui merci, j'avais pas vu.

Au final j'ai trouvé u_1(t)=\dfrac{Q_0}{C_2+C_1}(1-e^{\frac{-t}{\tau}})

Comme u_2(t)=\dfrac{-C_1u_1(t)}{C_2}, on a que u_2(t)=\dfrac{-C_1Q_0(1-e^\frac{-t}{\tau})}{(C_2+C_1)^2}

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 29-04-15 à 19:16

Sauf erreur de ma part pour u2 tu as
U2=(qo +c1u1)/c2

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 09:14

Ah, donc u_2=Q_0\dfrac{2-e^{\frac{-t}{\tau}}}{C_2(C_2+C_1)} ?

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 09:48

Et j'ai une petite question, en relisant la 5) je n'ai pas comprit pourquoi u_1-u_2+Ri=0? Et pas u_1+u_2+Ri=0?

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 11:23

euh oui coquille

Posté par
J-Pre : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 13:03

Avec le dessin de la question initiale.

U1 + U2 + R.i = 0

i = C1.dU1/dt = C2.dU2/dt

dU1/dt + dU2/dt + R.di/dt = 0

i/C1 + i/C2 + R.di/dt = 0

R.di/dt + i(1/C1 + 1/C2) = 0

di/dt + i.(C1+C2)/(R.C1.C2) = 0

i(t) = K*e^[-(C1+C2).t/(R.C1.C2)]

i(0) = - U1(0)/R

Or Qo = C1.U1(0)
U1(0) = Qo/C1

i(t) = -Qo/(R.C1) * e^[-(C1+C2).t/(R.C1.C2)]

i = C1.dU1/dt

dU1/dt = -Qo/(R.C1²) * e^[-(C1+C2).t/(R.C1.C2)]

U1(t) = K + Qo.RC1C2/((C1+C2)(R.C1²)) * e^[-(C1+C2).t/(R.C1.C2)]

U1(t) = K + Qo.C2/((C1+C2).C1) * e^[-(C1+C2).t/(R.C1.C2)]

U1(0) = Qo/C1

Qo/C1 = K + Qo.C2/((C1+C2).C1)
Qo/C1 ( 1 - C2/(C1+C2)) = K
K = Qo/(C1+C2)

U1(t) = Qo/(C1+C2) + Qo.C2/((C1+C2).C1) * e^[-(C1+C2).t/(R.C1.C2)]

U2 = -U1 - Ri

U2 = -Qo/(C1+C2) - Qo.C2/((C1+C2).C1) * e^[-(C1+C2).t/(R.C1.C2)] + Qo/C1 * e^[-(C1+C2).t/(R.C1.C2)]

U2 = -Qo/(C1+C2) - (Qo/C1).[C2/(C1+C2) - 1]* e^[-(C1+C2).t/(R.C1.C2)]

U2(t) = -Qo/(C1+C2) + Qo/(C1+C2) * e^[-(C1+C2).t/(R.C1.C2)]

U2(t) = -Qo/(C1+C2) * (1 - e^(-(C1+C2).t/(R.C1.C2)))

Groupement des résultats:

U1(t) = Qo/(C1+C2) + Qo.C2/((C1+C2).C1) * e^[-(C1+C2).t/(R.C1.C2)]
U2(t) = -Qo/(C1+C2) * (1 - e^(-(C1+C2).t/(R.C1.C2)))
i(t) = -Qo/(R.C1) * e^[-(C1+C2).t/(R.C1.C2)]
------

Et pour t--> +oo (on retrouve) :

i = 0
U1 = Qo/(C1+C2)
U2 = -Qo/(C1+C2)
-----

Toutes erreurs incluses (rien relu)

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 14:28

et pour les energies E=(1/2)Cu
donc
dE1= (1/2)C1 (u1(inf+)-u1(0))
dE2= (1/2)C2 (u2(inf+)-u2(0))

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 14:28

avec les carrés cest mieux
et pour les energies E=(1/2)Cu²
donc
dE1= (1/2)C1 (u1(inf+)²-u1(0)²)
dE2= (1/2)C2 (u2(inf+)²-u2(0)²)

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 14:44

D'accord, merci. Je pense avoir compris

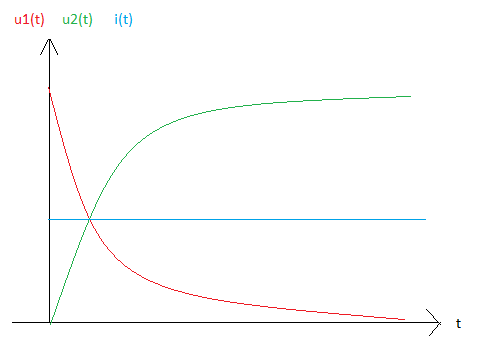
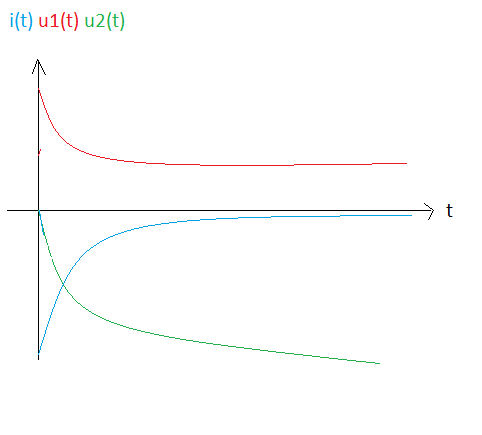
Pour le graphe, je pense que c'est ca, mais je ne suis pas du tout sure pour l'intensité i(t)

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 14:45

Ca pardon:

Étude d’un circuit avec condensateurs et résistance

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 14:50

Pour la 6), je pense que le signe de \DeltaE_1 <0 et \DeltaE_2>0 car C_1 se décharge et C_2 se charge.

C'est bien ca?

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 14:53

\Delta E_1 <0 et \Delta E_2 > 0

Désolée, un petit problème de latex...

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 14:56

non ton graphe est faux.
En tout cas pout i(t) qui n'ets pas constant.

Regardes les réponses de JP ,elles sont claires.

Après, u1 et u2 je sais pas, ou est l'axe des abscisse?
tu vois dans la réponses de JP, qu'en +inf, u1 et >0 et u2<0 ce qui n'a pas kl'air d'etre le cas sur ton dessin

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 15:20

C'est ca? Je ne vois pas du tout quelle peut être l'allure de i(t)...

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 15:21

:

Étude d’un circuit avec condensateurs et résistance

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 15:24

JP t'a donné:

U1(t) = Qo/(C1+C2) + Qo.C2/((C1+C2).C1) * e^[-(C1+C2).t/(R.C1.C2)]
U2(t) = -Qo/(C1+C2) * (1 - e^(-(C1+C2).t/(R.C1.C2)))
i(t) = -Qo/(R.C1) * e^[-(C1+C2).t/(R.C1.C2)]

ce sont 3 exponentielles.
Tu devrais arriver à les tracer !

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 15:31

Ben c'est ce que j'ai fais non?

Pour le i(t), je sais que c'est décroissant car c'est nègatif, mais je ne vois pas où la placer

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 15:39

i(t) = -Qo/(R.C1) * e^[-(C1+C2).t/(R.C1.C2)]

en 0, i vaut -Qo/(R.C1)
en +inf, il vaut 0

c'est docn une exponentielle CROISSANTE, qui pars d'une valeur negative, et qui tends vers 0*


Fais pareil pour les u
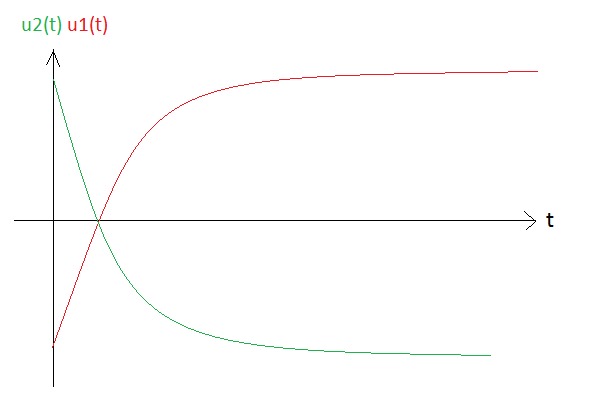
tes dessins sont faux:
en t=0 u2 vaut 0 et tends vers -Qo/(C1+C2) en +inf
en t=0 u1 vaut Qo/C1 et tends vers Qo/(C1+C2) en +inf

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 16:20

D'accord, merci.

Du coup j'ai essayé et ça m'a donné ça:

Étude d’un circuit avec condensateurs et résistance

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 16:25

u1 et u2 sont pas mal

i(t) est encore faux.
il par de -Qo/(R.C1) et va vers 0 !!!!!

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 16:27

euh non encore u1 est faux (il doit etre orinté dans l'autre sens)
il pars de Q0/C1 et il tends vers Qo/(C1+C2) qui est plus petit que la valeur de départ !!!

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 16:45

Ah oui pardon , j'avais lu l'inverse...

Du coup c'est ca?

Étude d’un circuit avec condensateurs et résistance

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 16:54

i et u2 ok

mais u1 doit etre orienté dans l'autre sens
sa valeur de depart et plus haute que sa valeur d'arrivée


Elle a cette forme:


*
**
   ***
      *****
           ***********
                     ********************************

Posté par
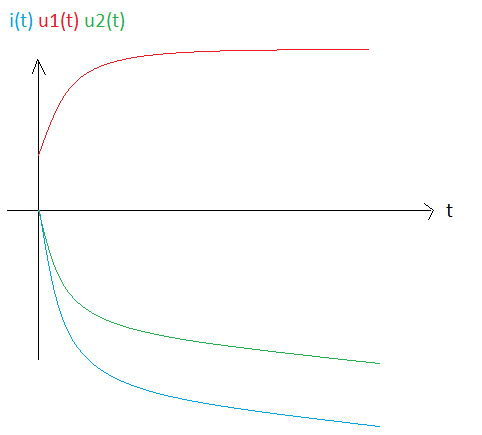
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 17:01

Pour l'effet joule, on a:

EJ=R\int_{0}^{+\infty}i(t)^2 dt = R[\dfrac{i(t)^3}{3}]_{0}^{+\infty} = R[\dfrac{Q_0}{RC_1}]

C'est bien ca?

Étude d’un circuit avec condensateurs et résistance

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 17:05

pour le graphe, la tete générale est bonne.
Dans l'absolu, il faut que tu "remonte" ta corube rouge car elle doit etre (à la fin) symetrique de la verte

Pour Joule oui pour al formules mais qd tu prends i^3 entre +inf et 0 ca donne pas ca
en +inf i vaut 0 ok
mais en 0, non, et tu dois en prendre le cube

Fais attention dans tes calculs! ne va pas trop vite...

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 17:08

Il y a un petit truc que je ne comprend pas, pour la 2^e question, j'avais trouvé que : i(0^+)=0 et u_1(0^+)+u_2(0^+)=0...
C'est pas ca?

Posté par
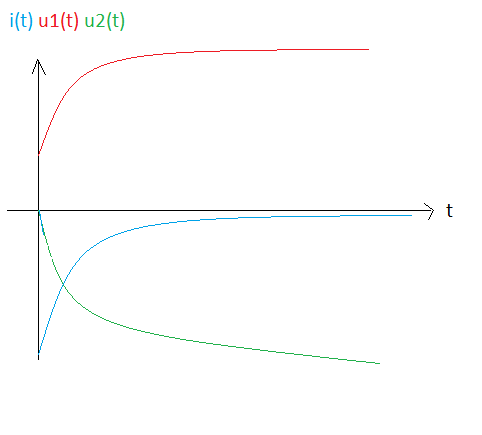
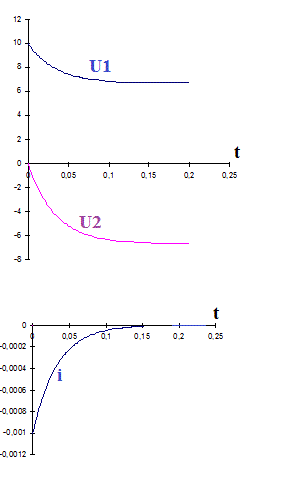
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 17:11

Oui, merci

Donc ca me donne : EJ=R\int_{0}^{+\infty}i(t)^2%20dt%20=%20R[\dfrac{i(t)^3}{3}]_{0}^{+\infty}%20=%20R[\dfrac{(\frac{Q_0}{RC_1})^3}{3}]=\dfrac{Q_0^3}{3R^2C_1^3}

Posté par
J-Pre : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 17:22

Exemple pour les graphes :

Comme C1, C2 et R  et Qo ne sont pas donnés, il faut bien les choisir pour pouvoir tracer les graphes.

Je choisis par exemple : C1 = 10^-5 F, C2 = 5.10^-6 F, R = 10^4 ohms et Qo = 10^-4 C

U1(t) = Qo/(C1+C2) + Qo.C2/((C1+C2).C1) * e^[-(C1+C2).t/(R.C1.C2)]
U2(t) = -Qo/(C1+C2) * (1 - e^(-(C1+C2).t/(R.C1.C2)))
i(t) = -Qo/(R.C1) * e^[-(C1+C2).t/(R.C1.C2)]

U1(t) = 6,67 + 3,33 * e^(-30.t)
U2(t) = -6,67 * (1 - e^(-30.t))
i(t) = -10^-3 * e^(-30.t)

tau = 1/30 s

Étude d’un circuit avec condensateurs et résistance

Ceci évidemment avec les conventions de signes imposées par le schéma de la question initiale.

Si on change certains sens de flèche sur le schéma donné au début, alors évidemment, il faudra en tenir compte ... et certaines courbes devront être "retournées".

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 17:30

non c'est u2(0)=0 et u1(0)=Qo/C1

Posté par
J-Pre : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 17:38

Attention, la réponse du 30-04-15 à 17:11 est tout à fait fausse.

Dans le calcul de l'intégrale, il faut remplacer i(t) par son expression dépendant de t soit donc i(t) = -Qo/(R.C1) * e^(-(C1+C2).t/(R.C1.C2))

EJ = R * \int_0^{\infty} [-Qo/(R.C1) * e^{-(C1+C2).t/(R.C1.C2)}]^2 dt ...

Le résultat devrait être être indépendant de la valeur de R (même si cela peut paraître étrange)

On devrait arriver à : EJ = Qo².C2/(2.C1.(C1+C2))

Sauf distraction.  

Posté par
MissMlleMoire : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 17:49

Merci

Mais quand on fait l'intégrale, on doit remplacer t par 0 et faire la limite de \dfrac{i(t)^3}{3} en +\infty non?

Posté par
gggg1234re : Étude d’un circuit avec condensateurs et résistance 30-04-15 à 17:51

qd tu intègres i(t)²

ca ne fait pas i(t)^3/3

il faut remplacer i(t) par sa valeur et l'integration est alors plus complexe.

Il faut que tu fasses attention, tu as des lacunes en calcul.

G.

1 2 +


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !