Inscription / Connexion Nouveau Sujet
Equilibre d'un solide mobile autour d'un axe de rotation
Bonsoir ,à tous.
S'ils vous plait aider sur cette exercice je ne sais pas comment determiner f .Notre prof nous a donné 3 jours de delai pour chercher 5 exercices sur ce chapitre s'ils vous plaît aidez moi à finir cet exo.Merci d'avance.
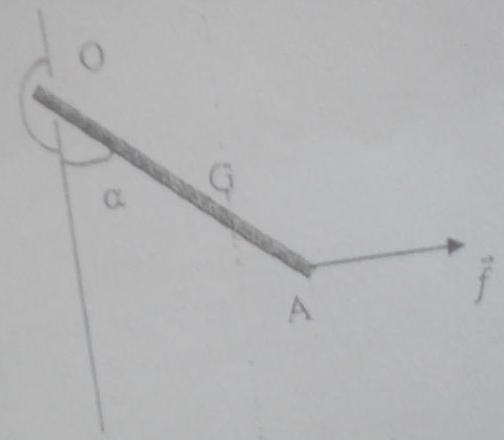
Exercice:
Quelle force f(vecteur) faut -il appliqué au point A pour que la barre AO de longueur
OA=2 OG=40cm, de poids P=2N, soit en equilibre autour d'un axe dans la position correspondant à l'angle  =30° ?.
=30° ?.
Bonsoir,
Il suffit d'écrire que la somme algébrique par rapport à l'axe O des moments des forces qui s'exercent sur cette barre est nulle.
On obtient une équation qu'il reste alors à résoudre pour répondre à la question posée.
La réaction de l'axe a une direction qui passe par cet axe. Son moment est nul.
Tes calculs des moments de et de
sont faux .
Il te faut donc revoir comment on calcule le moment d'une force par rapport à un axe.
As tu remarqué que tu n'as pas utilisé l'angle  entre la direction de la barre et la verticale ? Tu sembles donc admettre que le résultat ne dépend pas de cet angle.
entre la direction de la barre et la verticale ? Tu sembles donc admettre que le résultat ne dépend pas de cet angle.
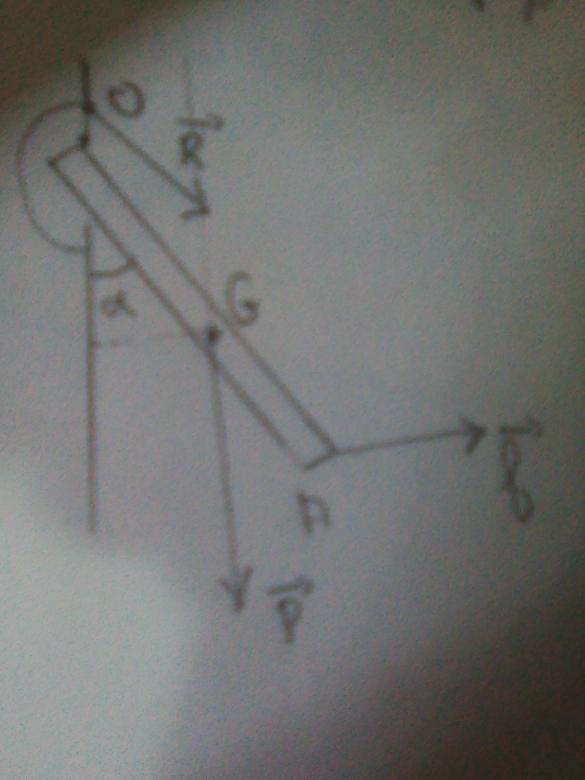
J'hesite: mais voila ce que je trouve :
M (P)+M
(P)+M (R)+M
(R)+M (f)=0
(f)=0
 P.OG=f.OA.
P.OG=f.OA.
Dois je cherché d1 et d2 ?
Voici mon shema:
Non
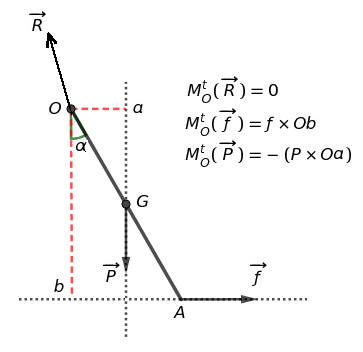
Pour calculer le moment d'une force par rapport à un axe la distance à prendre en considération est la distance entre cet axe et la droite qui porte la direction de la force.
Par exemple pour calculer le moment de la force par rapport à l'axe passant par O, on projette orthogonalement O en " b " sur la droite qui supporte
Voir le schéma ci-dessous.
Oui,
Si on se permet de modifier l'énoncé avec un poids de 2,0N alors
f = 2,0 * tan(30°) / 2 = 0,58 N
Sinon, si on conserve P = 2N alors f = 2 * tan(30°) / 2 = 0,6N
Bonne soirée !


