Inscription / Connexion Nouveau Sujet
Equilibre d'un solide mobile autour d'un axe
Bonsoir,
Je besoin encore d'un petit coup de main sur cet exo ,nous ferons un contrôle de Pc demain.
Exercice.
Les trois forces F1 ,F2 et F3(vecteurs) agissent sur une tige d'epaisseur negligeable et de longueur L=80cm aux positions l1, l2 et l3 à partir d'un pivot P situé à l'une des extremités.
1)Determiner le moment de chaque force par rapport au pivot.
2)Ecrire les conditions générales d'equilibre pour ce systeme et verifier si la tige est en equilibre.
Données:F1=30N ,F2=12N ,F3=10,3N;
 =25°,
=25°, =30° ,
=30° , =45°.
=45°.
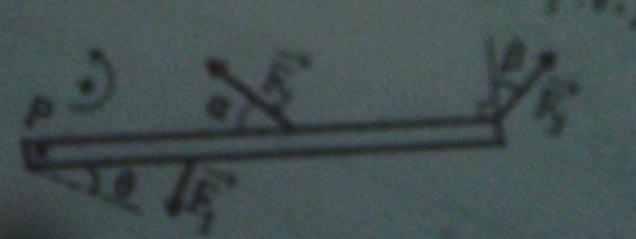
Desolé d'avoir des images de mauvaise qualités.
Dans cette figure je ne vois pas l'axe de rotation et aussi pourquoi il n y a pas des points (par exemple O,A ou G)je ne comprend pas à moins qu'il est encore bourré d'erreur.
La technique à mettre en œuvre est exactement le même que dans ton dernier exercice.
L'énoncé précise que l'axe de rotation est en P à l'extrémité de la tige.
Cette tige ayant une épaisseur négligeable on considère qu'elle a aussi un poids négligeable et c'est probablement pour cette raison que le centre de gravité n'est pas indiqué.
La tige est soumise à 4 forces :
La réaction du pivot qui s'applique en P
La force qui s'exerce en un point qui n'a pas reçu de nom, mais qui est situé sur la tige à la distance
2*L/5 = 32 cm de P. On peut appeler ce point " A " et on aura alors PA = 0,32m
On fait la même chose pour les forces et
dont les points d'application sont situés à 48 cm et 80 cm de P
Une fois les 4 moments calculés ( attention aux signes ) on fait leur somme algébrique pour savoir s'il y a ou non équilibre.
Bonsoir,
Mo(F1)+Mo(F2)+Mo(F3)+Mo(R)=0
Mo(F1)=-F1×PA.cos avec PA=L1
avec PA=L1
Mo(F2)=F2×PB.sin avec PB=L2
avec PB=L2
Mo(F3)=F3×PC.sin avec PC=L.
avec PC=L.
Mo(R)=0
(Sens anti horaire).
Bonsoir,
Mo(F1)+Mo(F2)+Mo(F3)+Mo(R)=0
Tu ne peux pas écrire cette égalité avant de l'avoir démontrée.
Mo(F1)=-F1×PA.cos avec PA=L1 = 2L/5
Mo(F2)=F2×PB.sin avec PB=L2 = 3L/5
Mo(F3)=F3×PC.sin avec PC=L.
Mo(R)=0
Tout cela est exact, il ne reste plus qu'à faire l'application numérique.
Tout cela est exact !
Comme indiqué dans mon post du 17/01 à 00h12 il ne te reste plus qu'à faire la somme des quatre moments pour savoir si la tige est en équilibre ou non.
Mo(F1)+Mo(F2)+Mo(F3)+Mo(R)=0
=>AN)
-8,7N.m+2,88N.m+5,82N.m=0
Comme on trouve 0 donc la tige est en equilibre.



