Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... École ingénieurForum supérieur ingé PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau école ingénieur
Partager :

Equation de Lagrange mécanique vibratoire

Posté par
Lauraunkut 21-11-19 à 13:28

Bonjour,

Après quelques mois de travail, je pense avoir enfin compris le fonctionnement de la mécanique vibratoire.

J'ai fais un exercice où il faut trouver les équations de mouvement grâce à la méthode de Lagrange.

\frac{d}{dt}(\frac{\partial T}{\partial {\dot{U_{i}}}})-\frac{\partial T}{\partial {{U_{i}}}}+\frac{\partial \Pi }{\partial {{U_{i}}}}=Q_{i}

La schéma est en image ci-dessous.
On considère que F(t)=0
J'ai trouvé comme équation de mouvement :

(\frac{m}{4}+\frac{m*b^{2}}{4*a^{2}}+\frac{m_{1}}{2}+\frac{m_{2}}{2}+\frac{m_{3}}{3}*\frac{a^{2}+b^{2}}{a^{2}})\ddot{U}+(\frac{Cr}{a^{2}}+\frac{Cr_{1}}{R_{1}^{2}}}+C)\dot{U}+(K+\frac{Kr_{2}}{R_{2}^{2}})U=0 \\

La masse m au centre de la plaque, est une masse ponctuelle.

Est-ce que c'est correct?
Ce sujet est un nouvel exercice, d'où le nouveau topic. Mais il est enlien avec ce topic
Problème mécanique vibratoire

Merci par avance.
Laura B***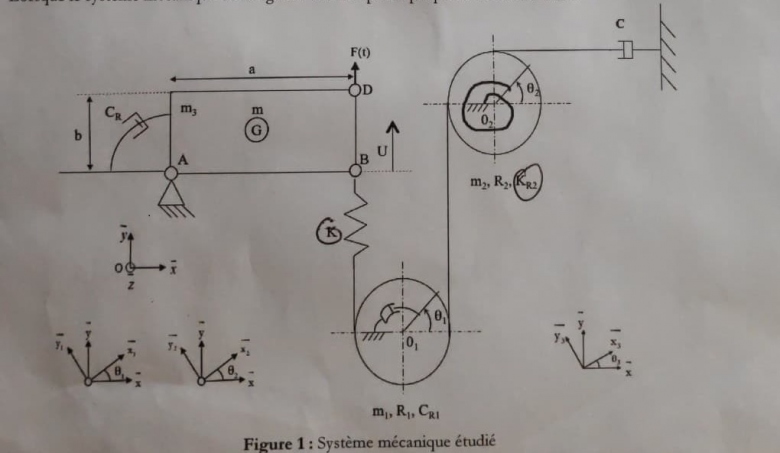

Equation de Lagrange mécanique vibratoire

Posté par
Lauraunkutre : Equation de Lagrange mécanique vibratoire 21-11-19 à 13:54

J'apporte quelques petites étapes à mes calculs.

Pour l'énergie cinétique :

T= T_{m} + T_{m1} + T_{m2} + T_{m3}

T_{m} =\begin{Bmatrix} \Omega (\beta 3/\beta)\\ \vec{V}(G \in m/R) \end{Bmatrix}_{G} . \begin{Bmatrix} \vec{V}(G \in m/R) \\ \sigma (G,m,R) \end{Bmatrix}_{G}
La masse étant ponctuelle, l'inertie est nulle.

\vec{V}(G \in m/R))=\vec{V}(A \in AB/R))+\vec{GA} \wedge\Omega (\beta _{3}/\beta )

\vec{V}(G \in m/R))=0+\begin{pmatrix} \frac{-a}{2}\\ \frac{-b}{2} \\ 0 \end{pmatrix}\wedge\begin{pmatrix} 0\\ 0\\ \frac{U}{a} \end{pmatrix}

T_{m}=\frac{1}{2}(\frac{m}{4}+\frac{mb^{2}}{4a^{2}})

T_{m1}=\frac{1}{2}(\frac{m_{1}}{2})

T_{m2}=\frac{1}{2}(\frac{m_{2}}{2})

T_{m3}=\frac{1}{2}(\frac{m_{3}}{3}\frac{(a^{2}+b^{2})}{a^{2}})

Posté par
vanoisere : Equation de Lagrange mécanique vibratoire 21-11-19 à 14:12

Bonjour
Dans le résultat que tu fourni, la somme des termes entre parenthèses que tu multiplies par la dérivée seconde de U par rapport au temps est correcte, ce qui laisse penser que tu as correctement évalué l'énergie cinétique du système. Pourtant les expression de Tm, Tm1... sont incomplètes...

Posté par
Lauraunkutre : Equation de Lagrange mécanique vibratoire 21-11-19 à 14:49

Aie Aie Aie, oui en effet, j'ai totalement oublié de mettre le U ^^
Ce qui deviendrais :

T_{m}=\frac{1}{2}(\frac{m}{4}+\frac{mb^{2}}{4a^{2}})\dot{U}^{2}
T_{m1}=\frac{1}{2}(\frac{m_{1}}{2})\dot{U}^{2}
T_{m2}=\frac{1}{2}(\frac{m_{2}}{2})\dot{U}^{2}
T_{m3}=\frac{1}{2}(\frac{m_{3}}{3}\frac{(a^{2}+b^{2})}{a^{2}})\dot{U}^{2}

Donc:
T=\frac{1}{2}(\frac{m}{4}+\frac{mb^{2}}{4a^{2}}+\frac{m_{1}}{2}+\frac{m_{2}}{2}+\frac{m_{3}}{3}\frac{(a^{2}+b^{2})}{a^{2}})\dot{U}^{2}

Ensuite :
\frac{\partial T}{\partial \dot{U}}=(\frac{m}{4}+\frac{mb^{2}}{4a^{2}}+\frac{m_{1}}{2}+\frac{m_{2}}{2}+\frac{m_{3}}{3}\frac{(a^{2}+b^{2})}{a^{2}})\dot{U}

Et pour finir:
\frac{d}{dt}(\frac{\partial T}{\partial \dot{U}})=(\frac{m}{4}+\frac{mb^{2}}{4a^{2}}+\frac{m_{1}}{2}+\frac{m_{2}}{2}+\frac{m_{3}}{3}\frac{(a^{2}+b^{2})}{a^{2}})\ddot{U}

La démarche est la même pour l'énergie potentielle, mais sans dérivée par rapport au temps.
Et aussi :
\frac{\partial T}{\partial U}=0


Est-ce que cette équation du mouvement vous semble correcte dans son intégralité ?

Merci pour tout vos conseils, car comme vous pouvez le constatez j'ai bien avancer depuis les messages de l'an passé.

Posté par
vanoisere : Equation de Lagrange mécanique vibratoire 21-11-19 à 15:07

Pas de problème pour les énergies cinétiques de m et m3. Pour les deux autres, tu sembles raisonner comme si le ressort de raideur K était inextensible. Le fait que le fil soit inextensible permet de poser :

\\ R_{1}.\theta_{1}=-R_{2}.\theta_{2}

mais cela ne permet pas de poser :

U=-R_{1}.\theta_{1}

L'allongement (au sens algébrique du terme) du ressort est a priori non nul et a pour expression générale :

\Delta L=U+R_{1}.\theta_{1}

Sous réserve d'avoir bien compris le problème... Sans énoncé complet...

Posté par
Lauraunkutre : Equation de Lagrange mécanique vibratoire 21-11-19 à 15:32

Autant pour moi, il est vrai que l'énoncé regorge d'informations essentielles...
Voici le sujet complet, mais il n'indique pas que le ressort est inextensible en effet, or dans tout les exercices que j'ai fait,il était considéré comme tel...

Le mouvement du système mécanique de la Fgure 1 est étudié par rapport au référentiel d'observation R=(O,\vec{x}\vec{y},\vec{z}). Soit \beta =(\vec{x},\vec{y},\vec{z}) la base associée à R. Le système est constitué par :


1. Un câble inextensible de masse négligeable (considérée nulle) qui relie le ressort de raideur K à l'amortisseur de constante d'amortissement C (figure 1).

2. Ce câble passe par deux poulies P1 et P2 de centre fixe O1 et O2, de masse respective m1 et m2 et de rayon respectif R1 et R2. Les poulies P1 et P2 sont respectivement reliées à un couple d'amortissement de constante Cr1 et à un couple résistif de constante Kr2 (figure 1). Les repères R_{1}=(O_{1},\vec{x_{1}}\vec{y_{1}},\vec{z_{1}}) de base \beta_{1} =(\vec{x_{1}},\vec{y_{1}},\vec{z_{1}}) et R_{2}=(O_{2},\vec{x_{2}}\vec{y_{2}},\vec{z_{2}}) de base \beta_{2} =(\vec{x_{2}},\vec{y_{2}},\vec{z_{2}}) sont respectivement liés aux poulies P1 et P2.

3. Une plaque ab de masse m3. Cette plaque est reliée à un pivot d'axe (A,z) en A et à un couple d'amortissement de constante Cr (figure 1). Seules de petites rotations, d'angle \theta _{3}, de la plaque autour de cet axe sont possibles. Soit R_{3}=(O_{3},\vec{x_{3}}\vec{y_{3}},\vec{z_{3}}) le repère lié à la plaque ab et \beta_{3} =(\vec{x_{3}},\vec{y_{3}},\vec{z_{3}}) la base associée a R3.

4. La plaque ab est munie d'une masse ponctuelle de masse m placée au centre de masse G, et est reliée en B à un ressort de raideur K. Au point D, une action F(t) est appliquée.

Lorsque le système mécanique de la figure 1 est au repos la plaque ab est horizontale.

Posté par
vanoisere : Equation de Lagrange mécanique vibratoire 21-11-19 à 16:42

Il est bien question de ressort de raideur K. L'allongement de ce ressort est susceptible de varier. Tu as donc un système avec deux variables de position : U et 1. Le système est équivalent à deux oscillateurs couplés grâce au ressort.

Posté par
Lauraunkutre : Equation de Lagrange mécanique vibratoire 21-11-19 à 16:52

Est-ce que je peux utiliser l'hypothèse des petits déplacements pour dire que tan(\theta _{3})=\theta _{3} =\frac{U}{a}?

Posté par
vanoisere : Equation de Lagrange mécanique vibratoire 21-11-19 à 16:59

Je pense que oui. Il s'agit ici d'étudier des vibrations de faibles amplitudes.

Posté par
Lauraunkutre : Equation de Lagrange mécanique vibratoire 21-11-19 à 17:11

Je vais retravailler encore dessus, je reviendrais quand j'aurai trouver la solution.

Merci

Posté par
gbm Webmasterre : Equation de Lagrange mécanique vibratoire 21-11-19 à 17:20

@Lauraunkut : merci pour la recopie de l'énoncé => j'ai supprimé en conséquence le message de l'ancien topic.

D'autre part, j'ai supprimé ton nom de famille de ta signature laissée en fin de message du 21-11-19 à 13:28 => en effet, même si on doit s'inscrire sur le forum pour poster un message, ces derniers restent publics et des personnes malveillantes sur le net pourraient tomber sur ton identité

Posté par
Lauraunkutre : Equation de Lagrange mécanique vibratoire 21-11-19 à 17:22

Merci beaucoup gbm, en effet, je n'avais pas réfléchie en mettant mon nom 😂

Posté par
Lauraunkutre : Equation de Lagrange mécanique vibratoire 25-11-19 à 22:29

Bonsoir, du coup j'ai retravaillé sur mon exercice, mais je trouve encore et toujours la même solution. J'ai revérifier la méthodologie que nous avions dans les précédents exercices, et les résultats sont similaires. Je vais tout de même détailler ma démarche, au cas où vous pourriez m'indiquez ou se situe l'erreur.

1 - Équation d'équilibre dynamique de Lagrange :

\frac{d}{dt}(\frac{\partial T}{\partial \dot{U_{i}}})-(\frac{\partial T}{\partial {U_{i}}})+(\frac{\partial \Pi }{\partial U_{i}})=Q_{i}

2 - Calcul de Qi, les forces excitatrices

\sum{\delta wnc}=\sum{Q_{i\delta U_{i}}}

\delta wnc = -C\dot{U}\delta U-Cr_1\dot{\theta _{1}}\delta \theta _{1}-Cr\dot{\theta _{3}}\delta \theta 3

\delta wnc = -C\dot{U}\delta U-Cr_1(\frac{\dot{U}}{r_{1}})\delta (\frac{U}{r_{1}})-Cr(\frac{\dot{U}}{a})\delta (\frac{U}{a})

Q=\frac{\sum{\delta wnc}}{\delta U_{i}}=(-C-\frac{Cr}{a^{2}}-\frac{Cr_{1}}{r_{1}^{2}})\dot{U}

3 - Calcul de l'énergie potentielle totale du système

\Pi =W+U avec W=0 car les forces conservatives sont négligées.

\Pi =U=\frac{1}{2}(KU^{2}+Kr_{2}\theta _{2}^{2})

\Pi =\frac{1}{2}(KU^{2}+Kr_{2}\frac{U^{2}}{r_{2}^{2}})

\Pi =\frac{1}{2}(K+\frac{Kr_{2}}{{r_{2}^{2}}})U^{2}

Donc on obtient :

\frac{\partial \Pi }{\partial U}=(K+\frac{Kr_{2}}{r_{2}^{2}})U

Pour finir, on calcule T, l'énergie cinétique totale du système :

T = Tm+Tm_{1}+Tm_{2}+Tm_{3}

      a. Calcul de Tm la masse ponctuelle :
Tm est une masse ponctuelle, donc son inertie est nulle.

Tm=\frac{1}{2}(m\vec{V}^{2}(G\in ab/R))

\vec{V}(G\in ab/R)=V(A\in ab/R)+\vec{GA}\wedge\Omega (\beta 3/\beta )

\vec{V}(G\in ab/R)=0+\begin{pmatrix} \frac{-a}{2}\\\frac{-b}{2} \\0 \end{pmatrix}\wedge\begin{pmatrix} 0\\0 \\\dot{\theta _{3}} \end{pmatrix}

\vec{V}(G\in ab/R)=(\frac{-b}{2}\dot{\theta _{3}}\vec{x_{3}}+\frac{a}{2}\dot{\theta _{3}}\vec{y_{3}})

On passe dans la base B.

\vec{V}(G\in ab/R) = (\frac{-b}{2}\dot{\theta _{3}}cos(\theta _{3})\vec{x}-\frac{b}{2}\dot{\theta _{3}}sin(\theta _{3})\vec{y}-\frac{a}{2}\dot{\theta _{3}}sin(\theta _{3})\vec{x}+\frac{a}{2}\dot{\theta _{3}}cos(\theta _{3})\vec{y})

On utilise l'hypothèse des petits déplacement :

\theta _{3}<<1\ ; \theta _{3}^{2}\approx 0\ ; cos(\theta _{3} )=1\ ; sin(\theta _{3})=\theta _{3}

Donc :

\vec{V}(G\in ab/R) = (\frac{-b}{2}\dot{\theta _{3}}\vec{x}-\frac{b}{2}\dot{\theta _{3}}\theta _{3}\vec{y}-\frac{a}{2}\dot{\theta _{3}}\theta _{3}\vec{x}+\frac{a}{2}\dot{\theta _{3}}\vec{y})

\vec{V}(G\in ab/R) = (\frac{-b}{2}\dot{\theta _{3}}-\frac{a}{2}\dot{\theta _{3}}\theta _{3})\vec{x}+(-\frac{b}{2}\dot{\theta _{3}}\theta _{3}\vec{y}\vec{x}+\frac{a}{2}\dot{\theta _{3}})\vec{y}

\vec{V}^{2}(G\in ab/R) = (\frac{-b}{2}\dot{\theta _{3}}-\frac{a}{2}\dot{\theta _{3}}\theta _{3})^{2}\vec{x}+(-\frac{b}{2}\dot{\theta _{3}}\theta _{3}\vec{y}\vec{x}+\frac{a}{2}\dot{\theta _{3}})^{2}\vec{y}

\vec{V}^{2}(G\in ab/R) = (\frac{b^{2}}{4}\dot{\theta _{3}}^{2}+\frac{a^{2}}{4}\dot{\theta _{3}}^{2}\theta _{3}^{2}+ab\dot{\theta _{3}}^{2}\theta _{3}+\frac{b^{2}}{4}\dot{\theta _{3}}^{2}\theta _{3}^{2}+\frac{a^{2}}{4}\dot{\theta _{3}}^{2}-ab\dot{\theta _{3}}^{2}\theta _{3})

\vec{V}^{2}(G\in ab/R) = (\frac{b^{2}}{4}\dot{\theta _{3}}^{2}+\frac{a^{2}}{4}\dot{\theta _{3}}^{2})

Tm =\frac{1}{2}(m (\frac{b^{2}}{4}\frac{\dot{U}^{2}}{a^{2}}+\frac{a^{2}}{4}\frac{\dot{U}^{2}}{a^{2}})

Tm =\frac{1}{2}(m\dot{U}^{2} (\frac{b^{2}}{4a^{2}}+\frac{a^{2}}{4a^{2}})

Tm =\frac{1}{2}(m\dot{U}^{2} (\frac{b^{2}}{4a^{2}}+\frac{1}{4})

    b . Calcul de Tm1 la poulie qui na pas de vitesse en translation

Tm_{1}=\frac{1}{2}\begin{Bmatrix} \Omega (\beta _{1}/\beta )& \\ \vec{V}(G_{1}\in P1/R) & \end{Bmatrix}_{G_{1}}.\begin{Bmatrix} m_{1}\vec{V}(G_{1}\in P1/R)& \\ \sigma (G_{1},P1,R) & \end{Bmatrix}_{G_{1}}

Tm_{1}=\frac{1}{2}(\Omega (\beta _{1}/\beta )*\sigma (G_{1},P1,R))=\begin{pmatrix} 0 &0 &\dot{\theta _{1}} \end{pmatrix}\begin{pmatrix} A &0 &0 \\0 &B & 0\\0 &0 &C \end{pmatrix}\begin{pmatrix} 0\\0 \\\dot{\theta _{1}} \end{pmatrix}=C\dot{\theta _{1}}^{2}

C dans le cas d'une matrice = \frac{MR^{2}}{2}

Tm_{1}=\frac{1}{2}(\frac{m_{1}r_{1}^{2}}{2}*\frac{\dot{U}^{2}}{r_{1}^{2}})=\frac{1}{2}(\dot{U}^{2}(\frac{m_{1}}{2}))

D'où:

Tm_{2}=\frac{1}{2}(\frac{m_{2}r_{2}^{2}}{2}*\frac{\dot{U}^{2}}{r_{2}^{2}})=[rouge]\frac{1}{2}(\dot{U}^{2}(\frac{m_{2}}{2}))

    c. Calcul de Tm3 la plaque.

Tm_{3}=\frac{1}{2}\begin{Bmatrix} \Omega (\beta _{3}/\beta )& \\ \vec{V}(A\in ab/R) & \end{Bmatrix}_{A}.\begin{Bmatrix} m_{3}\vec{V}(A\in ab/R)& \\ \sigma (A,ab,R) & \end{Bmatrix}_A

La vitesse au point A est nulle car le point A est fixe.

Tm_{3}=\frac{1}{2}(\Omega (\beta _{3}/\beta )*\sigma (A,ab,R))=\begin{pmatrix} 0 &0 &\dot{\theta _{3}} \end{pmatrix}\begin{pmatrix} A &0 &0 \\0 &B & 0\\0 &0 &C \end{pmatrix}\begin{pmatrix} 0\\0 \\\dot{\theta _{3}} \end{pmatrix}=C\dot{\theta _{3}}^{2}

C pour une plaque =\frac{m}{3}(a^{2}+b^{2})

Tm_{3}=\frac{1}{2}(\frac{m_{3}}{3}(a^{2}+b^{2})\dot{\theta _{3}}^{2})=\frac{1}{2}(\frac{m_{3}}{3}(a^{2}+b^{2})\frac{\dot{U}^{2}}{a^{2}}=\frac{1}{2}(\frac{m_{3}}{3}\frac{(a^{2}+b^{2})}{a^{2}}\dot{U}^{2})

On obtient donc un T total égal à :

T=\frac{1}{2}(\frac{m}{4}+\frac{mb^{2}}{4a^{2}}+\frac{m_{1}}{2}+\frac{m_{2}}{2}+\frac{m_{3}}{3}\frac{(a^{2}+b^{2})}{a^{2}})\dot{U}^{2}

Ensuite :

\frac{\partial T}{\partial U}=0

\frac{\partial T}{\partial \dot{U}}=(\frac{m}{4}+\frac{mb^{2}}{4a^{2}}+\frac{m_{1}}{2}+\frac{m_{2}}{2}+\frac{m_{3}}{3}\frac{(a^{2}+b^{2})}{a^{2}})\dot{U}

\frac{d}{dt}(\frac{\partial T}{\partial \dot{U}})=(\frac{m}{4}+\frac{mb^{2}}{4a^{2}}+\frac{m_{1}}{2}+\frac{m_{2}}{2}+\frac{m_{3}}{3}\frac{(a^{2}+b^{2})}{a^{2}})\ddot{U}

L'équation de mouvement est donc :

(\frac{m}{4}+\frac{mb^{2}}{4a^{2}}+\frac{m_{1}}{2}+\frac{m_{2}}{2}+\frac{m_{3}}{3}\frac{(a^{2}+b^{2})}{a^{2}})\ddot{U}+(C+\frac{Cr}{a^{2}}+\frac{Cr_{1}}{r_{1}^{2}})\dot{U}+(K+\frac{Kr_{2}}{r_{2}^{2}})U=0


Voila tout le détail de mes opérations, et franchement, je ne sais pas du tout où peut être l'erreur.

Merci par avance pour une réponse.

Posté par
vanoisere : Equation de Lagrange mécanique vibratoire 25-11-19 à 23:48

Pour l'énergie cinétique, tu sors vraiment “l'artillerie lourde” !

Chacun des trois solides est un solide en rotation autour d'un axe fixe et tu dois savoir que l'énergie cinétique dans ce cas vaut :

\frac{1}{2}I_{\Delta}.\omega^{2} : le demi produit du moment d'inertie par rapport à l'axe de rotation par le carré de la vitesse angulaire. Cela donne en une ligne :

T=\frac{1}{2}\left(I_{Az}.\frac{U^{2}}{a^{2}}+m_{1}.R_{1}^{2}.\dot{\theta}_{1}^{2}+m_{2}.R_{2}.\dot{\theta}_{2}^{2}\right)

C'est bien ce que tu as fait (en beaucoup plus long) et ton expression du moment d'inertie IAz de {m1,m3} est correcte. En revanche, tu n'as pas pris en compte mon message du 21-11-19 à 15:07 : la longueur du ressort varie. On peut donc poser :

R_{1}.\theta_{1}=-R_{2}.\theta_{2}

mais pas question décrire :   \textcolor {red}{U=-R_{1}.\theta_{1}}

Tu as donc un problème à deux coordonnées généralisées indépendantes U et 1. Cela conduit à :

T=\frac{1}{2}\left[I_{Az}.\frac{U^{2}}{a^{2}}+\left(m_{1}+m_{2}\right).R_{1}^{2}.\dot{\theta}_{1}^{2}\right]

Je te laisse remplacer le moment d'inertie en fonction de m1,m3, a et b comme tu as déjà été capable de le faire.

Cette erreur se répercute aussi au niveau de l'énergie potentielle. L'augmentation (au sens algébrique du terme) de longueur du ressort par rapport à la position correspondant à l'absence de vibration est, comme déjà dit :

\Delta L=U+R_{1}.\theta_{1}

Ce qui donne comme expression de l'énergie potentielle :

\\ \Pi=\frac{1}{2}K.\left(U+R_{1}.\theta_{1}\right)^{2}+\frac{1}{2}K_{R2}.\left(\frac{R_{1}}{R_{2}}\right)^{2}\cdot\dot{\theta}_{1}^{2}

Petite question pour voir si tu as bien compris : pourquoi cette expression de l'énergie potentielle, ne fait-elle pas apparaître explicitement l'énergie potentielle de pesanteur de {m1,m3}, a priori non négligeable ? Celle-ci vaut, à une constante arbitraire près :

\frac{1}{2}\left(m_{1}+m_{3}\right).g.U

Je te laisse réfléchir à tout cela...

Posté par
vanoisere : Equation de Lagrange mécanique vibratoire 26-11-19 à 14:06

Étourderie dans mon message précédent que je rectifie. Si on assimile chaque poulie à un disque homogène, son moment d'inertie par rapport à son axe de rotation est de la forme \frac{1}{2}m.R^{2}.  J'ai oublié les coefficients (1/2) dans les expressions de l'énergie cinétique. J'ai aussi oublié le "point" sur U... En revanche, tu n'avais pas commis ces étourderies !

T=\frac{1}{2}\left(I_{Az}.\frac{\dot{U}^{2}}{a^{2}}+\frac{1}{2}m_{1}.R_{1}^{2}.\dot{\theta}_{1}^{2}+\frac{1}{2}m_{2}.R_{2}.\dot{\theta}_{2}^{2}\right)

T=\frac{1}{2}\left[I_{Az}.\frac{\dot{U}^{2}}{a^{2}}+\left(\frac{m_{1}+m_{2}}{2}\right).R_{1}^{2}.\dot{\theta}_{1}^{2}\right]

Posté par
vanoisere : Equation de Lagrange mécanique vibratoire 27-11-19 à 14:03

Tu l'as sans doute déduit de toi-même mais je préfère quand même préciser : l'erreur que tu as commise en considérant le ressort de longueur fixe a aussi des répercussions sur l'expression de Q.
Pas de problème sur le terme en  \frac{C_{R}}{a^{2}}\dot{U} mais il faut revoir les deux autres termes. Il doivent être exprimés en fonction de \dot{\theta}_{1} car, comme déjà dit :

R_{1}.\delta\theta_{1}=-R_{2}.\delta\theta_{2}

mais

\delta U\neq-R_{1}.\delta\theta_{1}

Il faut bien faire attention sur le schéma aux orientations des angles. Puisque le fil est inextensible, une augmentation de 2 correspond à une diminution de 1 d'où le signe "-" ...

Posté par
Lauraunkutre : Equation de Lagrange mécanique vibratoire 09-01-20 à 17:10

Bonjour,

Désolé de ma réponse si tardive, j'ai essayé d'y retravaillé dessus, en fait on finit par avoir une équation avec 5 termes différents, \dot{\theta }; \ddot{\theta }; \dot{U} ; \ddot{U} et U.

C'est un partiel que j'ai passé, et je me disais bien que les résultats que j'avais me paraissaient trop simples. Je vais encore revoir mes cours pour repasser ce partiels, mais je n'ai pas encore les résultats.

Merci pour votre aide.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !