Bonjour
Pour la première partie :

La formule : est nécessairement fausse car elle n'est pas homogène : un déplacement ne peut être égal à un déplacement divisé par une longueur ! De plus tu ne précises pas de quel point de la poutre tu parles. Dans cette première partie, seule l'expression de u_c en fonction de u_a et u_b est nécessaire.
Il est alors simple d'obtenir l'expression de l'énergie cinétique.
Concernant l'énergie potentielle. Puisqu'il s'agit d'étudier les vibrations, u_a, u_b, u_c représentent les déplacement verticaux par rapport à la position d'équilibre horizontale de la poutre. Il faut commencer par déterminer le raccourcissement L de chaque ressort à l'équilibre en fonction de k,M et g. Les énergies potentielles des deux ressorts étant ensuite :


Quand on ajoute à ces deux énergies potentielles élastique les deux énergie potentielles de pesanteur, une simplification importante apparaît compte tenu de la condition d'équilibre précédente.
Une fois écrit le lagrangien, il est facile d'obtenir les deux équations différentielles recherchées.
Pour la seconde partie, il faut ajouter l'énergie cinétique et l'énergie potentielle de la poutre.

Petit schéma qui devrait t'aider à établir l'expression simple de u_c en fonction de u_a et u_b ...

Autant pour moi, l'expression pas homogène c'est parce que je n'ai pas écrit la fin :

Je ne comprend pas comment on arrive à cela
De plus je n'arrive pas à trouve Uc, donc difficile de trouver Uc'. Pour le reste je pense avoir compris mais je bloque sur Uc

De plus, je ne comprend pas les matrices dans la réponse, vient trouver

Pour le c'est mg/k mais je ne voit pas comment l'utiliser 😓

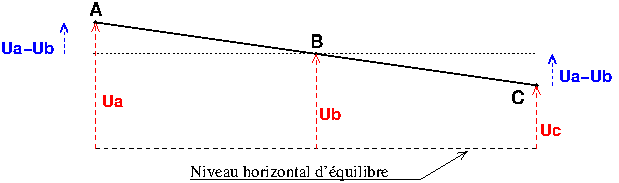
Pour u_c : la situation est simple : on voit bien sur le schéma que je t'ai fourni :


soit :


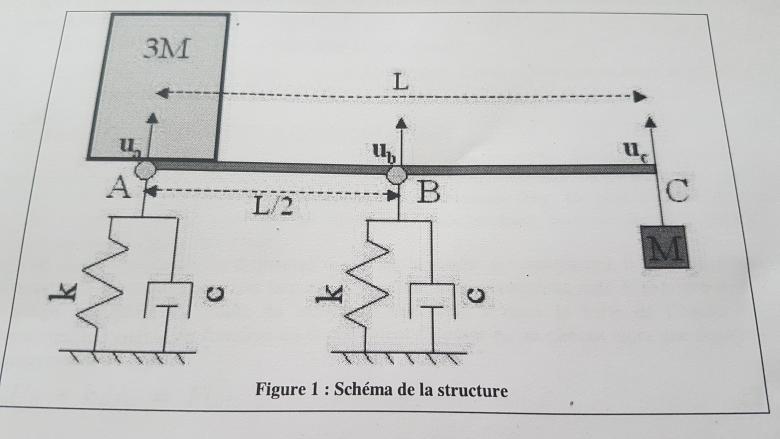
Pour un point de la poutre à la distance x de A, le schéma complété ci-dessous conduit à :



Cela conduit bien à la formule que tu as écrite.

Concernant les matrices, il s'agit juste d'une façon condensée d'écrire les deux équations différentielles vérifiées par les deux déplacements :




Pour l'étude de l'équilibre à l'horizontale de la poutre. En notant L_A et L_B les deux raccourcissements à l'équilibre, le fait que la résultante des forces soit le vecteur nul conduit à :



En considérant que la tige ne tourne pas autour d'un axe horizontal passant par A et perpendiculaire au plan de figure, le théorème des moments statiques conduit à :



Pour la suite, j'ai noté le raccourcissement commun aux deux ressorts.
Remarque : en regardant la figure, on peut supposer que les raccourcissements des deux ressorts à l'équilibre sont égaux mais il faut, je pense, faire la démonstration...

Pour l'énergie potentielle, il faut tenir compte des énergies potentielles élastiques et des énergies potentielles de pesanteur :



La relation d'équilibre : simplifie fortement l'expression de V.

Reste ensuite à appliquer le cours sur les propriétés du lagrangien...

Merci pour toutes c'est explications.
J'ai encore quelques soucis, U=Ua-y moi j'aurai pris y=xcos(a) et pas tan(a) pourquoi fait il prendre tan?
De plus, merci pour les matrices mais je ne comprend pas d'où sortent c'est 2 equa différentielles 😂 je crois que je suis fichue pour la mecanique

Je suis allé un peu vite dans ma démonstration...
Si x désigne la distance mesurée le long de la tige, il faut poser en toute rigueur :
y = x.sin().
Cependant, il ne faut pas oublier que l'on s'intéresse aux vibrations de faibles amplitudes : l'angle d'inclinaison de la poutre par rapport à l'horizontale est toujours très faible de sorte qu'il est possible de considérer dans les calculs le sinus égal à la tangente et le cosinus très voisin de 1.
As-tu étudié en cours la façon d'obtenir les équations différentielles vérifiées par les variables du problème à partir du Lagrangien ? Tu trouveras ce cours résumé ici , en particulier paragraphe 1.3 équation 14 :

autre document possible (équations avec efforts extérieurs) :

J'ai bien peur de t'avoir perturbé inutilement avec cette histoire de tangente sensiblement égale au sinus. Directement :

Merci beaucoup, ça va probleme du sinus est réglé, je vais lire le cours que tu a mis en lien, j'ai l'impression qu'il va m'aider, parce que mon cours n'est pas aussi détails donc je ne comprend pas grand chose 😀

Bonjour,

Je suis entrain de me replonger dans de vieux exercices de mécanique vibratoire, car je suis déterminée à comprendre, en sachant que je n'ai que peu de base.

J'ai la correction de cet exercice, mais j'aimerai, si vous le pouvez quelques explications, je suis obligée de reprendre du début pour comprendre, donc merci par avance.

Voici le sujet

"On étudie le comportement vibratoire d'une poutre rigide indéformable de masse m sur deux appuis élastiques (voir figure ci-dessous). L'appui en A supporte une structure de masse 3M. Pour équilibrer cette charge, on suspend à l'extrémité de la poutre une masse M.
1ère partie: équations du mouvement
Il est conseillé d'utiliser les équations de Lagrange et de paramétrer le système en fonction des déplacements Ua et Ub des points A et B.
a) Etude sans prise en compte des effets d'inertie de la poutre.
Dans cette partie, on ne considère pas les effets d'inertie de la poutre. En d'autre termes, la masse de la poutre m est négligeables par rapport à la masse M. Montrer que les équations du mouvements s'écrivent sous la forme:



Pour commencer, il faut chercher le déplacement d'un point de la poutre en fonction de Ua et Ub, ce qui donne :





Sur cette première partie j'ai déjà une interrogation, je n'arrive pas à comprendre pourquoi la dernière équation est comme ça. Si quelqu'un peut m'expliquer se serait génial.
Et pour la suite de cet exercice, cela viendra avec mes autres interrogations si quelqu'un est prêt à m'aider.

Merci infiniment, de la part d'une âme  égarée ^^



*** message déplacé ***

Bonjour

Franchement : tu te moques vraiment du monde ! Tu as posé exactement le même exercice il y a près d'un an. J'avais alors passé pas mal de temps  à essayer de t'aider ; tu n'en as absolument pas tenu compte puisque tu reproduis les mêmes erreurs !
Problème mécanique vibratoire

*** message déplacé ***

Je le sais, j'ai beaucoup réfléchis dessus et je ne comprend pas. Je n'ai pas de base en mécanique, c'est pour ça que je ne comprend pas...

*** message déplacé ***

Bonsoir,

Même un an après, les règles du forum s'appliquent toujours :

extrait de la FAQ du forum :

Q03 - Pourquoi ne faut-il pas faire du ''multi-post'' ?

Pour de nombreuses raisons.

Pour mémoire, le multi-post consiste à reposer une même question dans un sujet différent , ou à poser des questions successives d'un même problème dans des sujets différents.

De même, une demande identique sur plusieurs sites sera considérée comme un multipost et la discussion pourra être fermée par un modérateur.

Etant donné tous les désagréments créés par le multi-post, le non-respect de cette règle entraînera votre exclusion temporaire ou définitive du forum !

Voici maintenant quelques raisons qui font que nous combattons avec autant d'ardeur le multi-post (et ses adeptes ) :

• La perte de temps pour les modérateurs qui consacrent leur temps bénévolement pour garantir la qualité des sujets et des échanges sur le forum.
  
• Le respect du travail des correcteurs qui consacrent leur temps bénévolement pour aider ceux qui sollicitent de l'aide.
  
• La lisibilité du forum de manière à ce qu'un sujet ayant déjà reçu de l'aide soit facilement identifié et qu'un sujet n'en ayant pas encore reçu puisse à son tour en recevoir.

Rappelez-vous une nouvelle fois la règle d'or du forum :
1 sujet créé = 1 problème

Bonjour,

Vanoise, accepteriez-vous de m'aider sur ce problème ? Ce n'est pas pour vous faire perdre votre temps, bien au contraire. Mais cette matière me dépasse totalement et je ne comprend même pas le plus simple des problèmes.

Merci par avance

Es-tu à l'aise avec les notions fondamentales du programme de mécanique :
Pour le point matériel : lois de Newton, énergies cinétique et potentielle ;
Pour le solide : torseur cinétique et torseur dynamique ; équivalence du torseur dynamique et du torseur des actions extérieures ; énergies cinétique et potentielle ?
Ce n'est qu'ensuite qu'il est possible d'aborder le formalisme de Lagrange...

Je ne suis pas très à l'aise avec ces notions. C'est pour ça que j'essaye de faire des exercices "facile", pour essayer de comprendre tout cela.
J'ai énormément de mal sur les torseurs et les énergies cinétiques 😔

Tu as un résumé de cours de mécanique du solide ici :

Plus complet avec des exercices d'applications :

Autres exercices corrigés :

La liste pourrait s'allonger...

Je vais essayer de revoir ce cours avec les exercices ce soir, et je vous tiens au courant. Merci beaucoup

Re-bonjour,

Il y a quelque chose que je ne comprend pas dans le premier cours que vous m'avez envoyé, il est dit /
"Un point A', coïncidant au temps t avec le point A, fixe dans le référentiel Rrel a un mouvement, appelé mouvement d'entraînement, dans le référentiel  Rgal





Je ne comprend pas à quoi correspondent ce petit e et ce petit r.
Est-ce que c'est la vitesse d'entrainement et la vitesse relative?

Merci, je me suis rendue compte toute seule que c'était effectivement cela ^^

Bonjour Vanoise,

Je suis entrain de lire le cours (lien 2) que vous avez posté. J'ai quelques interrogation sur les premières parties.
1.  Lorsque l'on dit , le D correspond-il à la distribution de masse ?

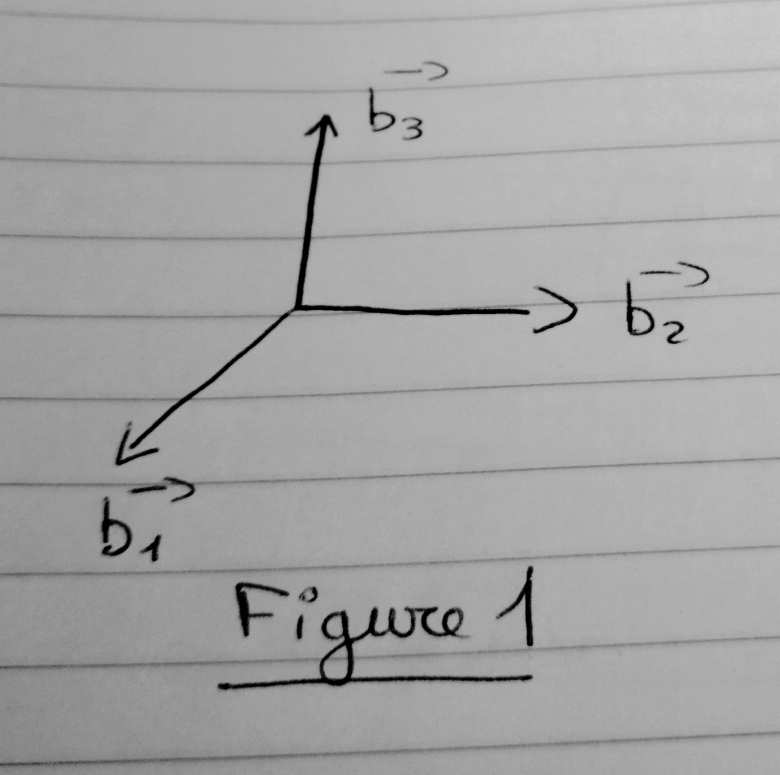
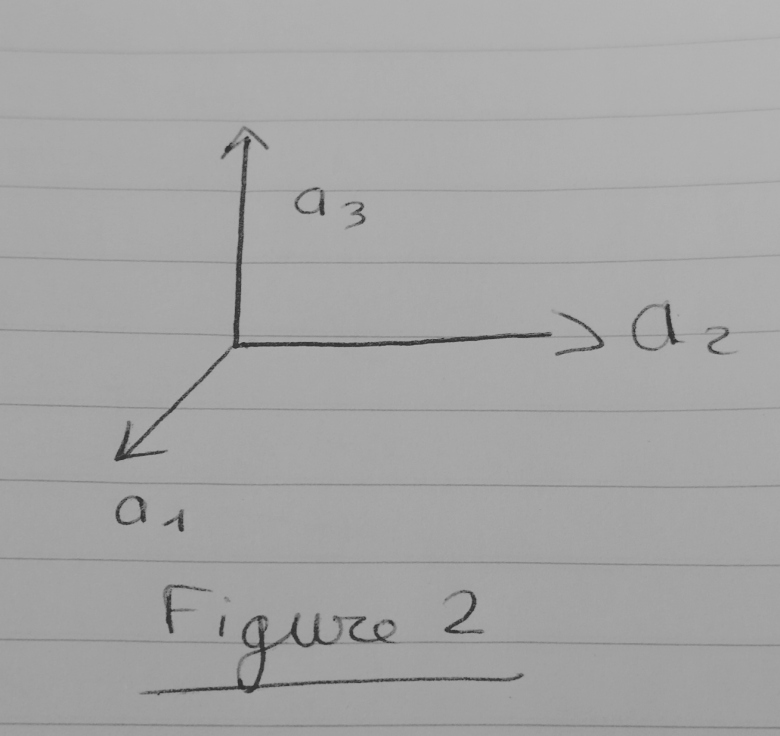
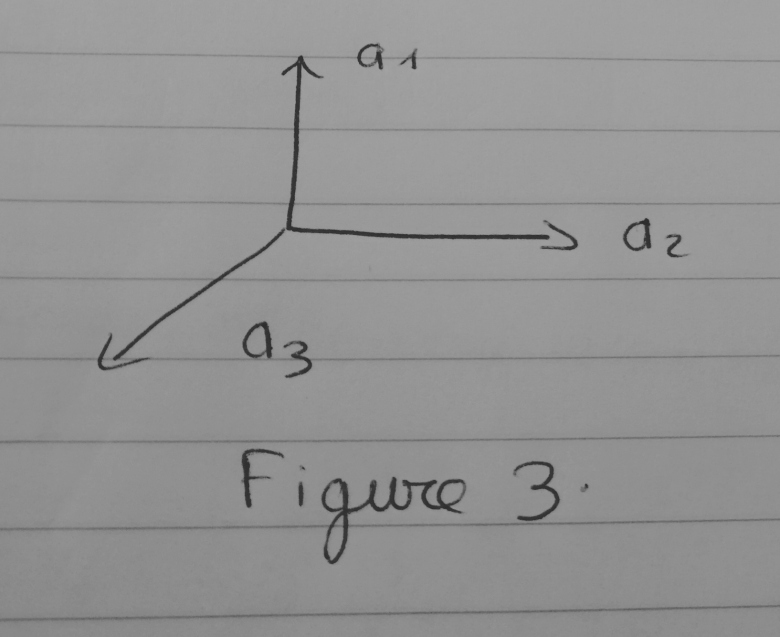
2.  Les bases sont toujours orthonormée et dans le sens direct : Cf figure 1

.
Dans cet énoncé je ne comprend pas pourquoi serait égal a zéro...

3.  Avec la figure 1 et la figure 2 on obtient

Mais avec la figure 1 et la figure 3, est-il correct de dire que l'on obtient :



4.  Il y a un petit exercice pour lequel je doute un peu, est-juste?

"On pose , exprimez en fonction de (x,y,z), puis et . "

Voici mes réponses:



Merci par avance ^^

Bonsoir
1° : Le D désigne le système étudié, c'est à dire la distribution de masse comme tu l'écris.
2° : le produit scalaire de deux vecteurs orthogonaux est le vecteur nul
3° : un même vecteur peut avoir des expressions différentes selon la base dans laquelle on l'exprime mais je ne comprends pas trop tes figures. Selon le document, a1, a2, a3 sont trois réels : les coordonnées du vecteur dans une base notée  
4° :  à mon avis, la réponse attendue à l'exercice II.1 est la suivante. Je te laisse la retrouver...

Bonjour bonjour,

J'ai enfin eu le temps de terminer de lire les cours que vous m'avez envoyé.
Je pensais avoir assez bien compris la théorie, j'ai donc décidé de refaire le premier exercice de mon cours, et là, c'est la catastrophe.
Voici l'énoncé, avec la correction que je n'arrive pas à comprendre, je ne retrouve pas du tout les réponses... Comment faire pour les retrouver, car je suis complètement perdue, je ne comprend plus a partir du moment ou je n'ai pas mon cours sous les yeux...

"Le système (figure 1) est soumis à un effort extérieur P(t) et à un couple Ces actions engendrent un déplacement U() de la masse m autour de sa position d'équilibre. Kr [N.m] et D [N.m.s] sont les constantes du couple résistif et du couple d'amortissement. Les deux poulies et ont respectivement une masse , et , un rayon et . Par ailleurs, on suppose qu'il n'y a pas de glissement entre les poulies et la corde. Ainsi toutes actions exercées par les poulies sur la corde s'appliquent dans les faits sur la masse m Ecrire les équations du mouvement en U(t) pour le système de la figure 1, par la méthode directe, la méthode des travaux virtuels et la méthode de Lagrange."

La correction indique qu'il faut faire le bilan des action mécaniques, et je trouve la même chose pour la formule :

Ensuite, il faut exprimer les valeurs du bilan, ce qui donne :
  
\vec{T} [/tex]   (Je ne comprend pas le negatif)
  (Je ne comprend pas le negatif)
  (Je ne comprend pas comment retrouver cette formule, j'ai beau cherché, je reste bredouille)

=   (Je ne comprend pas comme pour

=
(Je ne comprend pas comme pour et )

j'espère que j'ai étée assez claire, merci encore pour votre aide

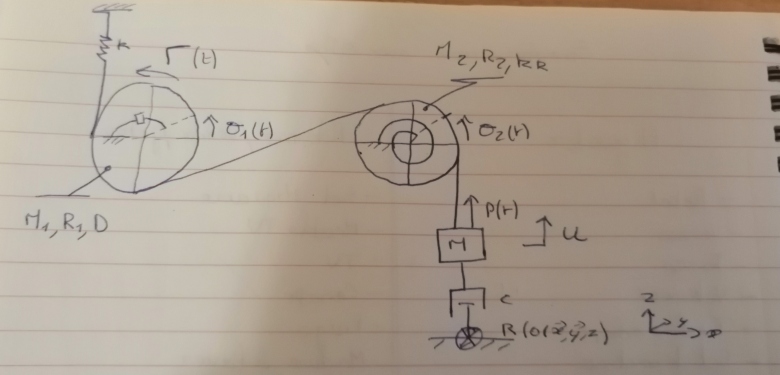
Bonsoir
Je ne comprends pas très bien ton corrigé. L'énoncé fournit les masses et les rayons des poulies. l'inertie des poulies n'est donc pas a priori négligeable. Il n'est donc pas a priori possible de faire un bilan global des actions mécaniques. Il faut décomposer le problème en trois :
1° Bilan des actions extérieures appliquée à la poulie 1 avec application du théorème du moment cinétique. Cela suppose de connaître le moment d'inertie de la poulie par rapport à son axe de rotation. Si la poulie est assimilable à  un disque homogène, ce moment d'inertie vaut 0,5.M₁.R₁².
2° Bilan des actions extérieures appliquée à la poulie n° 2 avec application du théorème du moment cinétique et prise en compte de son moment d'inertie.
3° Bilan des actions extérieures appliquées à la masse M en translation avec application de la RFD.
On relie ensuite ces trois relation en considérant que le fil est de masse négligeable : la norme de la tension du fil se conserve le long du brin entre les deux poulies et la tension se conserve le long du brin entre la poulie n° 2 et la masse M.
La force exercée par l'amortisseur de constante C'est une force de frottement donc une force de sens opposé à celui de la vitesse de M. En projection, cela donne bien une force proportionnelle à (-du/dt).
Le reste se justifie par application du théorème du moment cinétique à chacune des poulies . Manifestement ton corrigé néglige les inerties des deux poulies, ce qui revient à considérer leur moments d'inertie nuls.
La diplomatie m'empêche de dire ce que je pense de ton corrigé et l'exercice me parait un peu compliqué pour ton niveau...

Merci pour la rapidité de votre réponse, je regarde ça ce soir et demain soir.
Malheureusement, je pense que si on a pas de très solide base, on ne peut pas comprendre ce cours, et j'insiste sur le fait que cet exercice est le plus simple que notre prof ait donné 😂
Mais merci en tout cas

Pour t'aider un peu :
une vidéo très détaillée sur un système un peu plus simple :

Un peu plus difficile et peut-être pas à ton programme :

Voici ton schéma auquel j'ai ajouté les actions exercées par les différents brins du fil sur les trois solides à étudier.

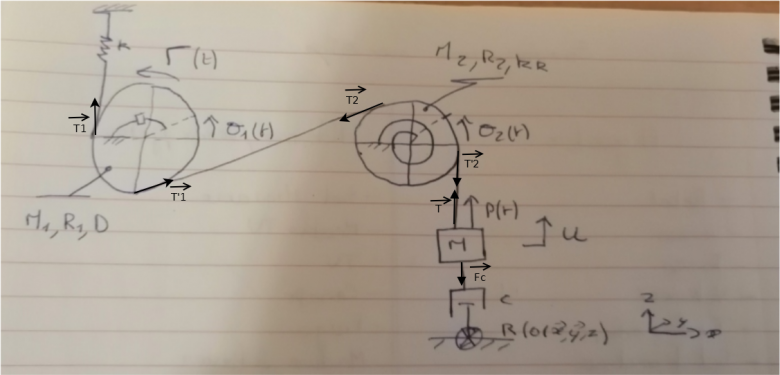
***Enoncé supprimé***

Bonjour,

1 sujet = 1 exercice, peux-tu créer un nouveau sujet pour ton énoncé d'exercice (tu as le droit de faire un renvoi vers le topic actuel pour le contexte si nécessaire) ?

Je supprimerai ce message d'ici ce soir.

Merci