Inscription / Connexion Nouveau Sujet
Energie mécanique
Bonjour est-ce-que vous pouvez m'aider ??
__________________________________________________________________________________________________
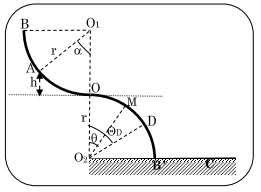
Une portion de gouttière BO de forme circulaire de rayon r=1m se situe dans un plan vertical. Elle se raccorde en O à une autre gouttière identique OB' située dans le meme plan(voir figure). Les centres O1 et O2 des deux gouttières se trouvce sur le meme plan horizontale passant par O . les frottement sont négligeables et g=10N/Kg
1) En choisissant le point O milieu de O1O2 comme origne ds altitudes et comme position de reference. Calculer l'energie mecanique du solide ;
2) Exprimer puis calculer la vitesse VO du solide au passage en O
3) Sur le parcours OD le solide reste en contact avec la surface de la gouttière et sa posistion est reperée par l'angle =(O2O, O2M).
Etablir l'expression de la vitesse V du solide en un point M quelconque du trajet OD en fonction de h, r ,g et
4) Sur le trajet OD on montre que l'intensité R de la reaction de la gouttière sur S a pour expression R=mg.(cos -v2/rg). Au point D le solide perd le contact avec la gouttière et suit le trajet DC. Determiner la valeur numerique D de et celle de Vc au point D.
5) A quelle vitesse le solide touche til le sol en C
_______________________________________________________________________________________________
Pour 1°/
Em=Epp+Ec
Ec=0
Em=m.g.h=0,2j
2°
puisque on néglige le frottement donc
Em(i)=Em(f)
Epp=Ec
m.g.h=0,5.m.vo²
v²=2.g.h
v²=4
v=2m/s
3°
j'ai essayé de travailler avec la conservation de l'énergie mécanique mais je sais pas comment trouver la hauteur en M est-ce-que vous pouvez m'aider?
Merci d'avance

Bonsoir,
Question 1 :
Comment as tu calculé l'énergie mécanique de ce solide puisque l'énoncé ne donne aucun renseignement à son sujet ?
Question 2 : Impossible donc de calculer la vitesse en O sans rien connaître du mouvement antérieur du solide.
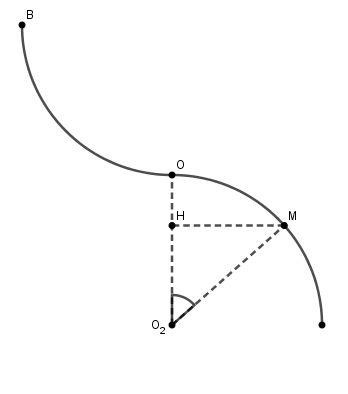
Question 3 : C'est une bonne idée que celle d'utiliser la conservation de l'énergie mécanique ( à condition de la connaître ! ). La dénivellation entre O et H ( voir figure ) se calcule comme la différence entre O2O et O2H
Question 1 :
L'énoncé ne donne ni la masse du solide, ni les renseignements qui permettraient de calculer l'altitude " h " de A par rapport à O , ni la vitesse au point A
Alors je renouvelle ma question.
Comment as tu calculé l'énergie mécanique que tu as trouvée être égale à 0,2J ?
Pardon j'ai copié l'exercice d'un site et je pense qu'il y a un manque de données
Voici l'énoncé:
_______________________________________________________________________________________________
Une portion de gouttière BO de forme circulaire de rayon 𝑟 = 1𝑚 se situe dans un plan
vertical.
Elle se raccorde en O à une autre gouttière
identique OB' située dans le même plan (voir
figure).
Les centres O1 et O2 des deux gouttières se
trouvent sur la même verticale.
Un solide ponctuel S de masse m=100g est
lâché sans vitesse du point A situé à une
hauteur ℎ = 0,2 𝑚 par rapport au plan
horizontal passant par O. Les frottements
étant supposés négligeables et g = 10N/Kg
1- En choisissant le point O comme origine des altitudes et comme position de
référence, calculer l'énergie mécanique du solide.
2- Exprimer puis calculer la vitesse du solide Vo au passage en O.
3- Sur le parcours OD le solide reste en contact avec la surface de la gouttière et sa
position est repéré par l'angle 𝜃 = (O2O,O[sub][/sub]2M ).
Etablir l'expression de la vitesse V du solide en un point M quelconque du trajet OD en
fonction de h , r , g et 𝜃.
4- Sur le trajet OD on montre que l'intensité R de la réaction de la gouttière sur S à
pour expression 𝑅 = 𝑚𝑔. (𝑐𝑜𝑠𝜃 −𝑉²/(𝑟.𝑔))
. Au point D le solide S perd le contact avec la
gouttière et suit le trajet DC. Déterminer la valeur numérique 𝜃𝐷 et celle de 𝑉𝐷 vitesse
du S au point D.
5- Avec quelle vitesse du solide touche-t-il le sol en C ?
_______________________________________________________________________________________________
Pardon encore
Evidemment ton nouvel énoncé change totalement la physionomie de l'exercice.
Tes réponses aux deux premières questions sont exactes.
Pour la question 3 tu peux appliquer la conservation de l'énergie mécanique entre A et M
Revoir mon post du 09-12-18 à 21:30 pour le calcul de la dénivellation entre O et H
Merci je pense que j'ai trouvé la réponse :
Puisque les frottements sont négligeables donc l'énergie mécanique se conserve
Em(i)=Em(f)
Et d'après la question 1
Em(i)=m.g.h
Et on a Em(f)=Ec+Epp
En M:
Ec=0,5.m.vm²
et
Epp=-m.g.(r-O2H)
Avec
r-O2H=r.(1-cos( )
)
Donc
Epp=-m.g.r.(1-cos( )
)
Alors Em(f)=0,5.m.vm²-m.g.r.(1-cos( )
)
Conservation de l'énergie mécanique :
m.g.h=0,5.m.vm²-m.g.r.(1-cos( )
)
m.g.h+m.g.r.(1-cos( )=0,5.m.vm²
)=0,5.m.vm²
m(g.h+g.r.(1-cos( ))=0,5.m.vm²
))=0,5.m.vm²
g.h+g.r.(1-cos( )=1/2.vm²
)=1/2.vm²
vm²=2.(g.h+g.r.(1-cos( ))
))
vm= (2.(g.h+g.r.(1-cos(
(2.(g.h+g.r.(1-cos( )))
)))
Est-ce-que c'est juste ??
Pour la question 4
Pour VD:
VD²=2.(g.h+g.r.(1-cos( )
)
VD²=2.(g.h+g.r.(1-VD²/g.r))
=2.g.h+2r.g-2VD²
3VD²=2.g.(r+h)
VD= ((2/3).g.(r+h)
((2/3).g.(r+h)
Pour  D:
D:
cos( ) = VD²/(g.r)
) = VD²/(g.r)
cos( ) = (2/3).g.(r+H))/(g.r)
) = (2/3).g.(r+H))/(g.r)
cos( ) = (2/3).(r+H))/r
) = (2/3).(r+H))/r
donc je vais calculer cos( )[sup]-1[/sup]
)[sup]-1[/sup]
J'ai pas encore calculer mais est - ce-que ma méthode est juste ??
Oui, tout est exact mais :
a) Il faut inverser la présentation et exprimer θD avant d'exprimer VD.
b) Il faut justifier soigneusement ces calculs, en particulier la raison pour laquelle tu écris que :
cos(θD)=(VD)2/ (gr)
a)D'accord
b)Au point D le solide s perd le contact avec la gouttière donc R=0
Donc cos(θD)=(VD)2/ (gr)
Peu importe !
L'énergie mécanique étant partout la même tu peux prendre n'importe quel point.
Ceci dit, le point de départ est probablement le plus commode.
Pardon j'ai une question
Dans l'énoncé de l'exercice la question 1:On choisissant le point O comme origine des altitudes et comme position de références.
est ce que cela veut dire que Epp=0?
Pardon j'ai une question
Dans l'énoncé de l'exercice la question 1:On choisissant le point O comme origine des altitudes et comme position de références.
est ce que cela veut dire que Epp=0?
si C'est ouii donc est ce que ce que j'ai fait est faux??

Oui, avec ce choix d'origines imposé par l'énoncé tu as :
Epp(B) = mgr
Epp(A) = mgh
Epp(O) = 0
Epp(B') = Epp(C) = -mgr
Les énergies potentielles de pesanteur dépendent de l'origine choisie, mais en revanche les variations d'énergie potentielles de pesanteur entre deux points quelconques n'en dépendent pas.
Pardon j'ai pas bien compris est ce que donc pour l'exercice 3 les étapes que j'ai fait sont faux ??
Rassure toi, tout tes résultats sont exacts.
En écrivant la conservation de l'énergie mécanique tu fais intervenir sans même t'en rendre compte une variation d'énergie potentielle.
Or cette variation est la même quelle que soit l'origine choisie (à condition bien entendu de ne pas en changer au cours de la démonstration).
Exemple :
Supposons que l'énoncé fixe l'origine des énergies potentielles en O2
alors :
Epp(B) = 2mgr
Epp(A) = mg(r+h)
Epp(O) = mgr
Epp(B') = Epp(C) = 0
Toutes les énergies potentielles ont changé, mais les variations sont restées les mêmes.


