Inscription / Connexion Nouveau Sujet
DM réfraction 1
Bonjour à tous j'ai un dm de physique à rendre pour lundi où je bloque dans certaines questions, les voici:
exercice 1:
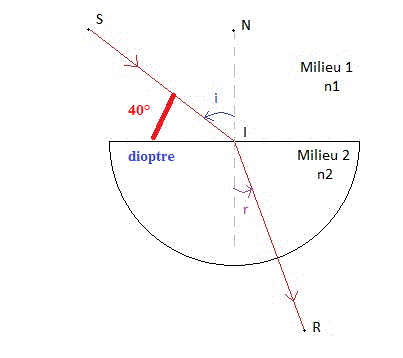
On considère le dioptre plan air/verre représente dans un plan perpendiculaire à sa surface. L'indice de l'air est égale à n1=1.00 et celui du verre à n2=1.50. Un rayon situé dans le plan de figure arrive sur ce dioptre, en faisant un angle de 40.0° avec le dioptre.
1/Calculer l'angle d'incidence i et le faire figurer sur un schéma respectant les différentes données et notations.
2/Écrire la deuxième loi de la réfraction et calculer l'angle de réfraction r puis tracer le rayon réfracté.
exercice 2:
***Enoncé effacé***
Merci d'avance, bonne journée.
***Un topic = un exercice***
Bonjour,
Tu ne bloques pas sur des questions, mais sur l'ensemble de ton DM ...
As-tu au moins fait un schéma de la situation ?
Représente :
* dioptre plan air/verre ;
* le rayon d'incidence avec son angle i ;
* le rayon réfracté avec son angle r
Je te conseille d'étudier attentivement cette fiche et de me faire des propositions de réponse ensuite :
![]() Réfraction de la lumière
Réfraction de la lumière
pas de problème, j'ai mis ça:
1/ angle d'incidence = 40°
2/ n1*sin i1=n2*sin i1
sin i1=(n2*sin i2)/n1
sin i1=(1.5*sin40)/1
sin i1=0.96
c'est bien ce que je me disais mais pourtant j'ai passé 10 minutes à réfléchir la dessus mais je ne sais pas comment faire autrement
mais la question 1/ est juste alors?
Mais i2 c'est ce que tu cherches à calculer, voilà pourquoi tu ne le connais pas 
La relation de Descartes doit être adaptée aux notations de l'énoncé :
n1*sin i1=n2*sin i2 s'écrit ici : n1.sin(i) = n2.sin(r)
<=> sin(r) = n1/n2.sin(i)
<=> r = sin-1(n1/n2.sin(i))
Il suffit d'utiliser ta calculatrice pour déterminer la valeur de l'angle (vérifie qu'elle soit bien réglée en degrés).

mais pourquoi passe t-on de
n1*sin i1=n2*sin i2 à sin i2=n1/n2*sin i1
et non de
n1*sin i1=n2*sin i2 à sin i2= n2/n1*sin i1
???
Oui, la fonction arcsin est une fonction comprise entre -1 et 1.
n1.sin(i) = n2.sin(r)
L'égalité est conservée si on multiplie chaque côté par une même constante :
<=> 1/n2.n1.sin(i) = 1/n2.n2.sin(r) tu es d'accord ?
Et donc n1/n2.sin(i) = sin(r).
Attends un peu, un dioptre est une surface séparant deux milieux transparents homogènes et isotropes, d'indices de réfraction différents. Donc, si le rayon incident fait un angle de 40° avec cette surface, que vaut l'angle d'incidence ?

donc le calcul serai:
n1/n2*sin(i)=sin(r)
donc1/1.5*sin40=sin(r)
donc 1.03=sin(r)
ce qui n'est pas possible
donc pour l'exercice 1:
1/ L'angle d'incidence est égale à 50°
2/ n1/n2*sin(i)=sin(r)
1/1.5*sin(50)=sin(r)
sin(r)=0.87
r=60.45°
L'angle réfracté est de 60.45°
C'est bien cela?
Comment est dévié le rayon quand tu passe d'un milieu moins réfringent à plus réfringent (n2 > n1) ?
j'ai refait les calculs et je trouve:
sin(r)=n1*sin(i)/n2
=1*sin(30)/1.5
=0.51
r=arcsin(0.51)
r=30.66°
Ahh ! Là je préfère  .
.
Retiens bien cette propriété de réfringence, c'est toujours utile pour s'assurer de la pertinence de ses résultats !
Une premier exercice de terminé ! Pense à cette propriété pour finir le deuxième.
Et pour vérifié ton résultat, tu peux utiliser de nouveau ta relation et vérifier que n1.sin(i) = n2.sin(r)
Eh ben voilà! 


Merci beaucoup j'ai enfin compris cet exercice 
Oui j'ai mis une proposition pour l'exercice 2 dans l'autre sujet
Merci beaucoup!