Inscription / Connexion Nouveau Sujet
DM : Le maître nageur et la jeune femme
Bonjour,
Je n'ai pas réussi à trouver ma réponse dans un autre topic similaire, c'est pourquoi j'en reposte un.
je vous écris l'énoncé en entier, mais je suis quand même parvenue à répondre aux questions 1 à 4, bien que mes calculs ne soient pas assez précis.
En fait, à partir de la question 5, je n'arrive pas à comprendre comment on peut calculer t1 et t2 avec des "calculs rigoureux" (car on l'a déjà fait dans les questions précédentes) ni quel est le rapport entre l'équation et le temps t.
Et je ne vois pas quelle conclusion donner à la question 6... 
Sujet :
Soit deux milieux : (1) une plage de sable et (2) la mer émeraude, séparés par un " dioptre cinématique ", la zone de fine marée autour de y=0. Un maître-nageur surveille l'étendue liquide. Soudain, il aperçoit une jeune femme en perdition. N'écoutant que son courage, il court vers elle.
Quelle est donc la trajectoire sur le sable et dans l'eau qui lui permettra d'atteindre son but en un temps minimal, compte tenu de la différence de vitesse des milieux ? Pour répondre à cette question, on trace les variations du temps de parcours total t pour différentes trajectoires.
Ces trajectoires diffèrent les unes des autres par le point de contact I du sauveteur avec l'eau.
Les coordonnées (en mètres) du maître nageur A sont : A(-50;50). Celles de la jeune femme : B(0;-50).
Les vitesses de déplacement du maître nageur sont : sur le sable, v1 6m/s et dans l'eau, v2 = 2m/s (il est motivé).
Soit t1 le temps mis par le maître nageur pour parcourir une première distance dans le milieu (1) à la vitesse v1 ; de même, soit t2 le temps mis par le maître nageur pour parcourir la seconde distance dans le milieu (2) à la vitesse v2.
Soit I(x,0) le point de contact du sauveteur avec le bord de l'eau en y=0 [m].
1. Relier la vitesse v1 à la distance AI et au temps t1. De même, relier v2 à t2 à IB.
2. En déduire l'expression du temps de parcours total t de A à B = t=t1+t2.
3. a) Recopier le schéma ci-dessus, avec une échelle suffisemment grande pour mesurer (avec une règle millimétrée) des distance AI et BI précisément. (Vous pouvez aussi calculer ces distances si vous le souhaitez).
b) Pour x variant de -50 m à 0 par pas de 5 m, mesurer les distances AI et IB. Calculer le temps total t = t1+t2. Dresser un tableau de résultats.
4. Représenter graphiquement la variation t=f(x). Prendre une échelle des ordonnées variant de t=35s à t= 45s, de façon à mieux déterminer la valeur du minimum xm par lequel passe la courbe. L'évaluer graphiquement. Soit Im le point de contact correspondant. En déduire la valeur du temps de parcours minimal tm.
5. Comparer la valeur trouvée de tm à la question précédente avec le temps que mettrait le maître nageur pour aller directement de A à B en ligne droite.
Pour répondre à cette question, faire une première évaluation graphique , puis effectuer le calcul rigoureux.
Indications: déterminer l'équation y = ax+b de la droite (AB), trouver son point d'intersection l' avec l'axe des abscisses, calculer les temps de parcours t1 et t2, puis t.
6. A partir de la valeur xm, calculer rigoureusement la valeur de sin i1, i1 étant l'angle que fait la trajectoire AIm avec la verticale ascendante. De même, calculer sin i2, i2 étant l'angle que fait ImB avec la verticale descendante. Comparer les valeurs sin i1/v1 et sin i2 / v2. Conclure.
Merci d'avance !
bonjour,
5) dès que tu connais I' tu connais t1 t2 et donc t=t1+t2
pour trouver I' le plus simple est d'utiliser le théorème de Thalès dans le triangle (ABH)
(cf dessin)
I'O  AH donc
AH donc
AH/I'O = BH/BO = 2 donc I'O=25 donc I'(-25;0)
d'où t1= AI'/v1 t2= I'B/v2
NB: pour trouver I' on peut aussi calculer l'éq. de (AB) puis l'intersection de (AB) et de (Ox) mais c'est plus lourd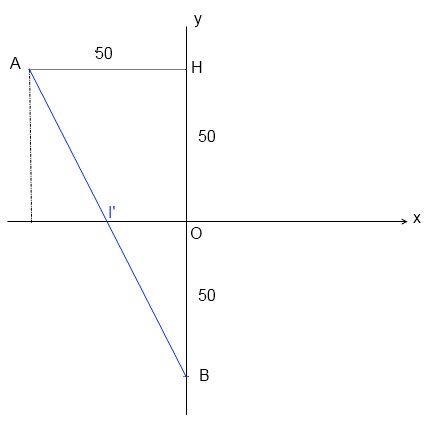
Edit Coll : image recadrée
Bonjour, et merci de votre réponse !
J'ai compris comment trouver I'. Mais je n'arrive toujours pas à comprendre pourquoi on doit calculer t1 et t2..
Dans quels cas doit on les calculer ? dans le cas de AI' ? AIm ..?
En fait, je connais déjà les valeurs de t1 et t2 car je les avais calculés dans la question 3.
Du coup, je comprends pas ce qu'on doit faire dans la question 5, si on doit répéter les mêmes calculs, ou bien s'il y a un rapport avec l'équation, et la position de I', rapport que je n'arrive pas à cerner.
Merci de votre patience !
dans la 3) tu as fait des mesures de distances pour en déduire des temps
dans la 5) on te demande d'abord de mesurer AI' et I'B pour évaluer t (tu l'as déjà fait dans le 3, effectivement, donc ça doit aller vite
puis de trouver ce même temps t uniquement par le calcul:
si le maître nageur va de A à I' puis de I' à B, sachant que sa vitesse est v1 entre A et I', et v2 entre I' et B
on trouve:
t1= AI'/v1 t2= I'B/v2
et t = t1+t2
mais là il faut calculer AI' à partir des coordonnées de A et de I' (et non pas mesurer AI' sur le dessin)
puis calculer I'B à partir des coordonnées de B et de I'



