Inscription / Connexion Nouveau Sujet
Calculer le travail dépensé par un tracteur pour avancer
Bonjour,
Toujours dans le même genre que l'exercice précédent, voici l'énoncé de l'exercice :
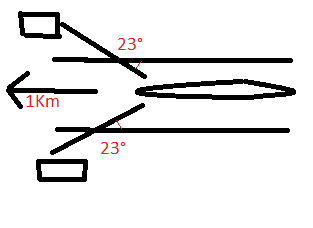
Un bateau est tiré par deux câbles au moyen de tracteurs qui roulent sur les chemins de halage. La traction dans chaque câble est de 5 kN. Les câbles font un angle de 23 ° avec les bords de la rive. Calculer le travail dépensé pour avancer de 1 km en l'absence de courant. Schématisez la situation.
Alors ici dans mon cours j'ai une autre formule.
W=F x deltaX x cosinus alfa
W= le travail
F=force exercée en newton
X= distance parcouru
le delta signifie ici distance final - distance initial
alfa représente l'angle dans l'énoncé.
Je n'ai pas réussi à réaliser cet exercice. Pouvez vous m'aider.
J'ai demandé à mes amis, et certains prenne comme valeur de l'angle 23° et d'autres 67 ° . Que faut il choisir ?
comment réaliser un schéma sur le site ?
Merci pour votre aide 
Bonjour,
Pour apprendre à insérer une image, une figure, un schéma, un graphique, un tableau (pas un énoncé !) clique sur la maison 
_______________
Un moyen possible pour calculer le travail d'une force dont le point d'application se déplace est :
est le produit scalaire du vecteur
qui représente une force par le vecteur
qui représente le déplacement du point d'application de cette force. Mais il est probable que tu n'as pas encore appris ce qu'est un produit scalaire.
La deuxième égalité montre l'une des manières de calculer ce produit scalaire.
est la norme de la force (un scalaire donc)
est la distance parcourue par le point d'application pour ce calcul de travail
est le cosinus de l'angle entre la force et le déplacement ;
. si 0 
< 90° l'angle est aigu, son cosinus positif et la force exerce un travail moteur.
. si 90° < 180° l'angle est obtus, son cosinus négatif et la force exerce un travail résistant.
. si a = 90° l'angle est droit, son cosinus est nul et la force n'exerce aucun travail.
Quand on veut déplacer "efficacement" un objet on a intérêt à utiliser l'angle le plus petit possible.
Quel dessin proposes-tu ?
Quel est le travail des forces exercées par les tracteurs ?
Non je n'ai pas vu le scalaire.
Alors, si je comprends bien il faut juste remplacer les données que l'on nous donne dans la formule :
Données : = 1000m (unité SI)
= 23°
F=5kN=5000N (unité SI)
Je remplace ça dans la formule et ça me donne :
W=5000 1000
Cos23°
W=4602524,267 N
w=4602kN pour un seul tracteur
4602kN 2 = 9205 kN pour les 2 tracteurs.
J'ai juste remplacé, mais je ne comprends la formule. Sinon est ce bon ?
Merci
Très bon dessin.
Tu as positionné l'angle tel qu'il est défini par l'énoncé.
Pour le physicien, l'angle intéressant est celui entre le vecteur déplacement (ta flèche marquée "1 km") et l'un ou l'autre des vecteurs forces (portés par les cables de traction). Mais l'angle du physicien se déduira très facilement par la géométrie (angle alterne-interne) de l'angle que tu as noté.
Continue !
Encore merci pour toutes ces explications et de la motivation que vous m'apportez.
La réponses est-elle bonne?
Annuler
connectez vous