Inscription / Connexion Nouveau Sujet
Calcul des angles d'incidences
Bonjours, pouvez-vous m'aider à résoudre cet exercice:
Lors d'une mesure on fait varier i(1) jusqu'à avoir i(4)=90°, on peut ainsi déterminer l'indice n en mesurant i(1).
L'indice de réfraction de l'aire est pris égal à 1,000.
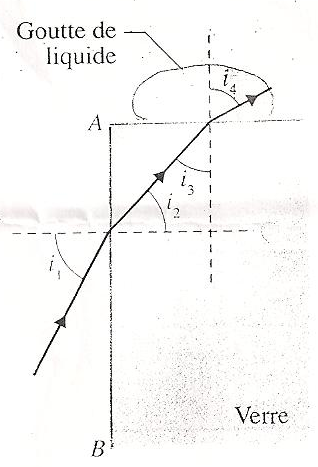
On a déposé une goutte de glycérine sur le bloc de verre d'indice N=1.652. On mesure i(1)=48.06°.
1) Calculer i(2)
2) Quelle est la valeur de i(3)
3)Sachant que i(4)=90°, déduire l'indice du liquide
Merci.
Tu pourrais poster le schéma ? parce que comme ça i(1), i(2), i(3) et i(4) c'est pas évident de savoir où ils sont placés.
ah c'est déjà mieux.
Bon on connait l'indice de réfraction de l'air et du verre, et l'angle d'incidence i(1), on utilise les lois de Snell-Descartes pour trouver l'angle réfracté i(2):
n1.sin(i(1))=n2.sin(i(2)) avec n1=nair=1,000 et n2=N=1,652
On a: sin( i(1))= N.sin( i(2)) <=> sin( i(2))= (1/N)*sin( i(1))
<=> i(2)= arcsin[ (1/N)*sin( i(1))]
Je te laisse calculer i(2) grâce aux données de l'énoncé ( arcsin c'est la touche sin-1 sur la calculatrice).
Pour trouver l'angle i(3), on remarque que les deux angles i(2) et i(3) sont dans un triangle rectangle, donc on va utiliser une propriété sur les angles dans un triangle:
180=90+ i(2) + i(3)
<=> i(3)=90-i(2)
Je te laisse encore calculer i(3) en fonction du résultat précédent.
Pour calculer l'indice du liquide, on utilise encore une fois les lois de Snell-Descartes en connaissant les deux angles i(3) et i(4) et un indice de réfraction N, il ne reste qu'une inconnue, je pense que ce genre de calcul ne doit poser aucun problème.
Pour résumer, quand on fait un exercice d'optique que l'on peut qualifier de géométrique (comme cet exercice), on écrit toujours les lois de Snell-Descartes pour la réfraction et la réflexion (là où il y a réflexion et réfraction), ensuite on utilise s'il n'y a plus réfraction ou réflexion entre deux angles, une relation géométrique dans un triangle (en général un triangle rectangle).
Ok c'est pas grave, tu as surement vu en cours les lois de Descartes:
i1=r l'angle incident est égale à l'angle réfléchi
n1.sini1=n2.sini2 relation liant les angles incident et réfracté.
Pour la première question, on a un rayon passant d'un milieu 1,ici l'air, à un milieu 2, ici le verre, cela veut dire qu'il y a réfraction donc que l'on peut utiliser la loi de Descartes liant les angles incident et réfracté.
On utilise la relation: n1.sin(i1)=n2.sin(i2) en prenant comme valeur de n1=1,000 car le milieu 1 est l'air et n2=N pour le milieu 2.
On cherche l'angle i2, on va isoler alors essayer d'isoler i2 dans cette équation, on isole d'abord sin(i2):
sin (i2)= (1/N).sin (i1)
Pour avoir i2 maintenant que sin (i2) soit isolé, il faut prendre l'arcsin des deux cotés de l'équation puisque arcsin (sin (i2))=i2.
On a alors i2= arcsin ((1/N).sin(i1))
Application numérique: i2=arcsin ((1/1,652).sin(48,06))=26,76°
Maintenant que l'on a la valeur de i2, on peut facilement trouver la valeur de l'angle i3, car on remarque un triangle rectangle formé par les deux normales au dioptre et le rayon lumineux à travers le verre.
On sait que la somme des angles d'un triangle est égale à 180°:
180°=90°+i2+i3
<=> i3=180-90-i2
<=>i3=90-26,76
<=>i3=63,24°
Pour trouver la valeur de l'indice de réfraction du liquide on utilise la même formule que pour la 1ere question puisqu'il y a réfraction entre le verre et le liquide:
N.sin(i3)=n4.sin(i4)
on cherche la valeur de n4 puisqu'on a calculé i3 et que N et i4 sont donnés.
n4=N.((sin(i3)/(sin(i4))
n4=1,652*(sin(63,24)/sin(90))
n4=1,475