Inscription / Connexion Nouveau Sujet
Balançoire moments de force
Salut
Pouvez vous m'aider pour un exercice sur le moment des forces ? merci bien
Exercice
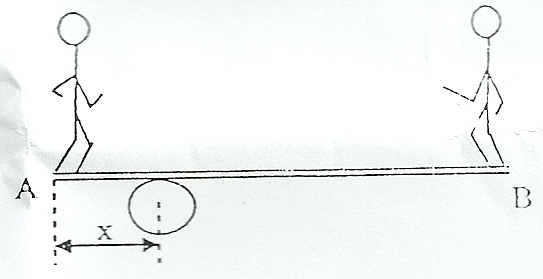
Une balançoire est constituée par une planche homogène de masse m = 10 kg et de longueur l = 3,2 m. Deux enfants, ABOU et BIAN, de masses respectives mA = 40 kg et mB = 30 kg sont assis aux extrémités A et B.
On place un rondin de bois à la distance x de A de sorte que l'équilibre de la balance soit réalisé en position horizontale.
1. Faire le bilan des forces qui s'exercent sur la balançoire. Les représenter sur un schéma.
2. Expliquer les moments de ces forces par rapport à l'axe du rondin.
3. Déterminer la distance x lorsque l'équilibre est réalisé.
Merci d'avance
Bonjour Sid07,
tu habites dans un bien beau pays... et je ne désespère pas d'y aller un jour.
Pour le bilan des forces, c'est très simple : il y en a quatre, le poids de Abou, celui de Bian, celui de la planche, et la réaction du sommet du rondin au point de contact avec la planche. Les trois premières sont verticales et dirigées vers le bas, la réaction
est verticale et dirigée vers le haut.
Le système est en équilibre, donc (mA + mB + m)g + R = 0 (je mets les vecteurs en gras, c'est plus commode). En projetant sur un axe vertical, orienté par exemple vers le haut, on obtient facilement R = mB + m)g.
Pour la suite, j'ai besoin de savoir comment on t'a expliqué ce qu'est le moment d'une force. Peux-tu me dire ce que tu sais à ce sujet ?
3)
masse de la partie de la poutre de longueur x: m1 = m * x/3,2
masse de l'autre partie de la poutre : m2 = m * (3,2-x)/3,2
moment des forces par rapport au point de pivot :
M = m2.g .(3,2-x)/2 + mB.g.(3,2 - x) - m1.g * x/2 - mA.g.x
Il y a équilibre si M = 0, donc si : m2.(3,2-x)/2 + mB.(3,2 - x) = m1 * x/2 + mA.x
m2.(3,2-x)/2 + mB.(3,2 - x) = m1 * x/2 + mA.x
10 * (3,2-x)²/6,4 + 30 * (3,2 - x) = 10.x²/(2*3,2) + 40.x
Equation qui résolue donne : x = 1,4 m
-----
Recopier sans comprendre est inutile.
Sauf distraction. 
Bonjour Sid bonjour et bonne année à tous.
2. Expliquer les moments de ces forces par rapport à l'axe du rondin.
Pour la 3, J-P a raisonné en considérant séparément le poids de chacune des deux parties de la planche, on peut aussi résoudre le problème en prenant en compte le poids de la planche dans son ensemble, c'est ce qu'avait commencé à faire PrBeBo, je continue sur cette voie.
En choisissant comme sens positif pour la rotation autour de l'axe, le sens des aiguilles d'une montre, on a, pour la 2) :
Le moment de
Pour la 3), on écrit, qu'à l'équilibre, la somme des moments par rapport à l'axe est nulle ce qui donne :
soit, après simplification par
çàd, finalement :
L'application numérique donne bien
Au revoir


