Inscription / Connexion Nouveau Sujet
Angle d'énergie
Bonjour à tous, j'ai besoin de votre aide s'il vous plait :
Je dois déterminer l'angle d'énergie reçue au sol en w/m². Je dois faire un tableau et un graphique de l'énergie reçue au sol en w/m² en fonction de l'angle d'incidence de la lampe.
1m² : angle 23.26° : 2,56m²
1m² : angle 70,26° : 1,06m²
1m² : angle 90 ° : 1m²
Je ne sais pas comment effectuer les calculs. il faut savoir combien fait 1m² par watt ?
Je suis complètement perdu et je compte sur votre aide.
Merci beaucoup.
Bonjour Bastien44.
Votre demande est bien peu claire, je n'ai jamais entendu parler "d'angle d'énergie".
Quant à vos données...
1m² : angle 23.26° : 2,56m²
1m² : angle 70,26° : 1,06m²
1m² : angle 90 ° : 1m²
Je crois comprendre qu'il s'agit d'étudier la façon dont l'énergie fournie par un source lumineuse se répartit sur une surface éclairée par cette source, en fonction de l'angle d'incidence.
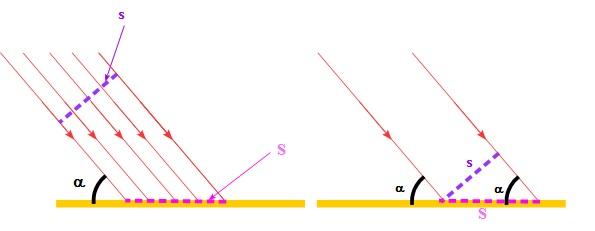
Si c'est bien de cela qu'il s'agit, voici un schéma qui devrait vous aider à y voir plus clair (cf ci-dessous).
On considère que la source lumineuse émet un faisceau de lumière faisant avec le sol un angle
 .
.
La puissance de la source est telle qu'une puissance de 1 W, se répartit sur une surface s (orthogonale aux rayons lumineux).
Si on désigne par S, la surface éclairée (au sol) par la source, quelle relation simple lie, s, S et
 ?
?
La puissance produite par la source lumineuse (1 W), se répartit sur cette surface S ; la puissance par unité de surface de sol éclairé est alors p = 1/S, avec p en W.m-2 et S en m2.
Une fois que vous aurez trouvé cette relation, faites un tableau regroupant quelques valeurs de
 , S et la puissance par unité de surface p.
, S et la puissance par unité de surface p.| S (m2) | p (W.m-2) | |
| 10 | ||
| 20 | ||
| 30 |
A vous.
A oui, j'oublie le graphe...
Pour conclure, faites une courbe représentant les variations de p en fonction de  .
.
J'ai limité le tableau à 3 valeurs de  , il faudra bien entendu le compléter avec d'autres valeurs pour disposer au minimum d'une huitaine de points sur la courbe.
, il faudra bien entendu le compléter avec d'autres valeurs pour disposer au minimum d'une huitaine de points sur la courbe.
A plus.
Bonjour bastien44, et bonjour picard  ,
,
j'avais un peu regardé ce problème hier soir et, ne sachant pas non plus ce qu'est un angle d'énergie (aucune trace sur le web), j'ai juste fait une figure que je poste ci-dessous (évidemment elle ressemble à la tienne picard !).
J'ai l'impression que cet exercice doit avoir comme support concret l'orientation de panneaux solaires ou de cellules voltaïques, mais pour l'angle d'énergie, là... ignorance de notre part ou élucubration du prof (si si, ça peut aussi arriver) ? De plus les trois lignes données par bastien44 n'éclairent pas notre lanterne.
Bon, je livre quand même le maigre fruit de mes réflexions :
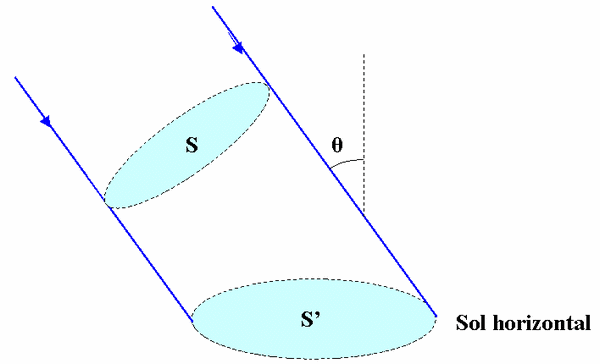
Sur la figure ci-dessous, j'ai dessiné un faisceau de rayons dont la section droite a une aire S et qui arrive sur le sol horizontal en faisant un angle  avec la verticale. La surface projetée sur le sol est S', avec S' > S, et on peut montrer sans trop de peine que S = S'.cos
avec la verticale. La surface projetée sur le sol est S', avec S' > S, et on peut montrer sans trop de peine que S = S'.cos (bastien44, remplace le cercle par un carré qui par projection devient un rectangle, et ça ira).
(bastien44, remplace le cercle par un carré qui par projection devient un rectangle, et ça ira).
Donc S' = S/cos .
.
La dernière ligne de données de l'énoncé (1m2 = 1m2 pour  = 90°) montre que l'angle
= 90°) montre que l'angle  est mesuré par rapport à l'horizontale, ce que la figure de picard confirme. Donc mon angle
est mesuré par rapport à l'horizontale, ce que la figure de picard confirme. Donc mon angle  vaut 90° -
vaut 90° -  , soit cos
, soit cos = sin
= sin (pour bastien44 : pas de pb avec la trigonométrie ?). Donc S' = S/sin
(pour bastien44 : pas de pb avec la trigonométrie ?). Donc S' = S/sin .
.
Prenons un faisceau incident d'aire S = 1 m2. Alors on peut calculer S' en écrivant S' = 1/sin , et on trouve ceci :
, et on trouve ceci :
 = 23,26°
= 23,26°  S' = 2,53 m2 ;
S' = 2,53 m2 ;
 = 70,26°
= 70,26°  S' = 1,06 m2 ;
S' = 1,06 m2 ;
 = 90°
= 90°  S' = S = 1 m2.
S' = S = 1 m2.
Les valeurs numériques données par bastien44 sont donc retrouvées. Quant aux W par m2 qui représentent un puissance radiative par unité de surface (pour bastien : une puissance radiative est une puissance apportée - ou perdue - par rayonnement), je ne vois pas où elles vont intervenir dans ce pb, mais peut-être que toi, picard, tu as trouvé : il faut aussi prendre une puissance incidente de 1 W (avec mon S = 1 m2 on a bien une puissance par unité de surface de 1 W.m-2) et regarder comment elle "s'étale" sur une surface plus grande lorsque les rayons incidents sont obliques.
Si c'est ça, le jeu consiste à tracer sin en fonction de
en fonction de  ...
...
Bastien44, si tu pouvais apporter un peu de lumière à notre lanterne (en W.m-2 si tu veux  ), ce serait bien.
), ce serait bien.
Pour info : le Soleil envoie sur Terre une puissance radiative de 1360 W.m-2 en incidence normale ( = 0 ou
= 0 ou  = 90°). Cette valeur est une moyenne annuelle car elle dépend de la distance Terre-Soleil. En été sous notre latitude, à midi la direction du Soleil fait avec la verticale un angle
= 90°). Cette valeur est une moyenne annuelle car elle dépend de la distance Terre-Soleil. En été sous notre latitude, à midi la direction du Soleil fait avec la verticale un angle  proche de 30°. La puissance radiative qui arrive au sommet de l'atmosphère terrestre est alors environ 1180 W.m-2. Seul 80% de cette puissance arrivera au sol, le reste étant absorbé par l'ozone de la stratosphère, réfléchi vers le ciel par les nuages, et autres raisons selon la composition de l'atmosphère.
proche de 30°. La puissance radiative qui arrive au sommet de l'atmosphère terrestre est alors environ 1180 W.m-2. Seul 80% de cette puissance arrivera au sol, le reste étant absorbé par l'ozone de la stratosphère, réfléchi vers le ciel par les nuages, et autres raisons selon la composition de l'atmosphère.
Je ne suis pas sûr d'avoir fait progresser le schmilblick, mais bon... cette réponse m'aura au moins occupé pendant 20 mn !
Bonjour, bonsoir!
Désolé pour ma réponse tardive, les cours ne me permettent pas de me connecter ( réseau internet sécurisé .. )
Je vous remercie pour vous réponses.
Les données que j'ai cité correspondent à trois dessins différents sur lesquels ( par exemple 2.51 m² ) à une feuille et un faisceau de lumière de 1m² dont l'angle est 23.26 ° éclairant ainsi 2,51 m²?
De même pour un faisceau de 1m² positionné à 70,26° par rapport à la feuille éclairant 1,06 m².
Et enfin un faisceau de 1m² positionné à 90° par rapport à la feuille éclairant 1m².
Faut-il multiplier l'angle par le m² ?
Bonne soirée
Prenez le temps de lire les réponses que vous avez obtenues, cela devrait vous permettre d'avancer.
Faut-il multiplier l'angle par le m² ?
Je suis d'accord avec la réaction de picard :
pour la relation entre l'angle  et la surface correspondante, on est tous les trois d'accord pour dire qu'on l'a trouvée. Le problème qui se pose maintenant est : qu'est-ce qu'on fait avec ça ? En d'autres termes : 1) que veut dire "angle d'énergie" (définition introuvable) ? 2) qu'est-ce que ton professeur attend de toi ? L'énergie en W.m-2 qui arrive qu sol dépend de deux facteurs : a, l'énergie transportée par le faisceau ; b, l'angle avec lequel elle atteint la surface réceptrice. Tant que tu ne nous auras pas renseigné sur ce que tu dois faire, tu n'as aucune chance de trouver quelqu'un pour le faire à ta place... on attend tes réponses.
et la surface correspondante, on est tous les trois d'accord pour dire qu'on l'a trouvée. Le problème qui se pose maintenant est : qu'est-ce qu'on fait avec ça ? En d'autres termes : 1) que veut dire "angle d'énergie" (définition introuvable) ? 2) qu'est-ce que ton professeur attend de toi ? L'énergie en W.m-2 qui arrive qu sol dépend de deux facteurs : a, l'énergie transportée par le faisceau ; b, l'angle avec lequel elle atteint la surface réceptrice. Tant que tu ne nous auras pas renseigné sur ce que tu dois faire, tu n'as aucune chance de trouver quelqu'un pour le faire à ta place... on attend tes réponses.


