Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Exercice sur un circuit RLC

Posté par
Marc_Benford 01-12-12 à 23:22

Bonjour.

J'ai un exo sur ce circuit là :
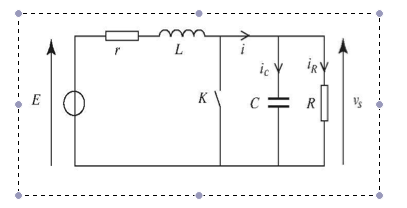
Exercice sur un circuit RLC


Ils demandent tout d'abords, lorsque l'interrupteur est fermé depuis assez longtemps pour que le régime permanent soit atteint, de trouver la charge du condensateur et d'en déduire Vs, puis de trouver le courant qui traverse la bobine.
Je sais juste que q = C*Vs soit Vs = q / c mais je n'ai aucune idée de ce que vaut q...
Par contre pour le courant qui traverse la bobine j'ai une petite idée : comme on est en régime permanent i(bobine) = cte donc di(bobine)/dt = 0 et d'après la relation Ul = L*di(bobine)/dt + r*i on trouve i(bobine) = Ul / r mais ça me semble bof bof..

Puis ils nous demandent d'établir l'équation différentielle vérifiée par Vs lorsqu'à l'instant t=0 on ouvre l'interrupteur, sans utiliser q, ic, ir, i.
J'ai utilisé la loi des mailles : E = Vs + Ul
E = Vs + L*di/dt + r*i
Puis la loi des noeuds : i = ic + ir
i = C*dVs/dt + Vs/R
Puis je dérive i et je remplace dans la première équation et ça donne :
E = LC*(d^2Vs/dt^2) + (L/R + rC)*dVs/dt + (r/R + 1)*Vs
Ca parait un peu compliqué mais j'ai 'impression que c'est ça.

Et enfin, il faut donner la valeur de Vs et de i, quand t tend vers l'infini. Et il faut donner la valeur critique de r en fonction de L, R et C.
D'après l'équation différentielle je dirais que Vs(t->infini) = (E*R) / (r+R)
Par contre pour la valeur critique je vois pas. Il doit y avoir une formule que je connais pas.


Bref, merci d'avance si vous pouvez m'aider !

Edit Coll : image placée sur le serveur de l' Merci d'en faire autant la prochaine fois !     

Posté par
efpere : Exercice sur un circuit RLC 01-12-12 à 23:58

salut

quand l'interrupteur est fermé depuis assez longtemps, alors ce qui est à sa droite est en cour-circuit donc Uc = 0 V donc q = 0 C

pour l'équa diff c'est bien ce que tu as trouvé.

en effet à t infini on va arriver à l'équivalent d'un pont diviseur de tension, d'où la formule qu'on retrouve. et i tendra vers E/(r+R)

pour la valeur critique de r, j'ai pas trop d'idée. Il s'agit peut-être de la valeur de r qui annule le discriminant du polynome caractéristique de l'équation diff

Posté par
Marc_Benfordre : Exercice sur un circuit RLC 02-12-12 à 03:09

Merci pour ta réponse !


Mais en faite, si comme tu dis quand l'interrupteur est fermé depuis assez longtemps il n'y a plus rien qui passe dans ce qui est à droite, alors d'après la loi des mailles on a : E = Vs + Ul
E = Ul (car Vs = 0)
E = L*di/dt + r*i (i étant le courant qui traverse la bobine)
E = r*i (car j'imagine que i = cte)
i = E/r
C'est juste ?


Pour la valeur critique, je crois que r(critique) = 2\sqrt{L/C} (j'ai vérifié et c'est homogène en unité)
Mais c'est un peu bizarre vu qu'ils demandent de calculer la résistance critique "en fonction de R, L et C" (et pas seulement L et C)..


En faite après ils demandent de tracer le graphe de Vs quand r = r(critique) et quand r << r(critique).
Je crois que quand r = r(critique) la courbe est un peu comme ça :

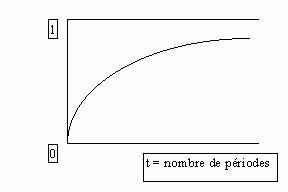
Exercice sur un circuit RLC

Avec l'asymptote qui coupe l'axe des ordonnées en (E*R) / (r+R).
Et puis quand r << r(critique) c'est la même chose sauf qu'il y à des petites oscillations de plus en plus petites.

Par contre, ils demandent ensuite dans le cas où r << r(critique) de calculer la pseudo-période et la constante de temps. Ils nous donnent les valeurs de r, R, L et C, mais je vois pas trop comment trouver...
Pour la constante de temps j'ai pensé à calculer dVs/dt quand t=0 (pour avoir la tangente à l'origine) puis d'essayer de voir pour quel t cette droite coupe l'asymptote, mais je n'ai aucune idée comment faire..

Edit Coll : image placée sur le serveur de l' Merci d'en faire autant la prochaine fois !     

Posté par
efpere : Exercice sur un circuit RLC 02-12-12 à 11:42

salut

Citation :
Mais en faite, si comme tu dis quand l'interrupteur est fermé depuis assez longtemps il n'y a plus rien qui passe dans ce qui est à droite, alors d'après la loi des mailles on a : E = Vs + Ul
E = Ul (car Vs = 0)
E = L*di/dt + r*i (i étant le courant qui traverse la bobine)
E = r*i (car j'imagine que i = cte)
i = E/r
C'est juste ?


oui c'est juste

Citation :
Pour la valeur critique, je crois que r(critique) = 2 (j'ai vérifié et c'est homogène en unité)
Mais c'est un peu bizarre vu qu'ils demandent de calculer la résistance critique "en fonction de R, L et C" (et pas seulement L et C)..


la valeur critique de r est celle qui annule = b²-4ac

pour la pseudo période et la constante de temps tu as des formules dans ton cours normalement

Posté par
Marc_Benfordre : Exercice sur un circuit RLC 02-12-12 à 13:10

Citation :
la valeur critique de r est celle qui annule = b²-4ac
J'ai essayé de faire le calcul, et après un temps assez long j'ai trouvé qu'il y avait deux solutions :
r(critique) = L/(RC) + 2\sqrt{L/C}
et r(critique) = L/(RC) - 2\sqrt{L/C}
Ca ressemble presque à la formule que j'ai trouvé sur un site sauf que c'est pas exactement ça...


Citation :
pour la pseudo période et la constante de temps tu as des formules dans ton cours normalement
Euh en faite un problème fait que je n'ai pas de cours pour ça encore.. Est-ce que pour la pseudo-période c'est ça : T = 2π\sqrt{LC} (= 2π / ω0) ?
Et pour la constante de temps j'aurais dis Tau = \sqrt{LC} mais ça ressemble trop à l'autre expression..

Posté par
Marc35re : Exercice sur un circuit RLC 02-12-12 à 15:23

Bonjour,
L'équation caractéristique de l'équation différentielle sans second membre est quelque chose de la forme :
\alpha\,x^2\,+\,\beta\,x\,+\,\gamma\,=\,0
(j'ai utilisé x au lieu de r, comme on le fait souvent, puisque r est déjà utilisé pour une résistance)
On peut calculer le discriminant.

\Delta\,>\,0  régime apériodique
Les racines sont de la forme :
\large x\,=\,\frac{-\,\beta\,\pm\,\sqrt{\Delta}}{2\,\alpha}

\Delta\,=\,0  régime apériodique critique
Les racines sont de la forme :
\large x\,=\,\frac{-\,\beta}{2\,\alpha}

\Delta\,<\,0  régime oscillatoire amorti
Les racines sont de la forme :
\large x\,=\,\frac{-\,\beta\,\pm\,j\,\sqrt{-\,\Delta}}{2\,\alpha}
Dans ce cas, on trouve comme solution une exponentielle à argument négatif multiplié par une fonction sinusoïdale (un cosinus sans doute).
La constante de temps est dans l'argument de l'exponentielle.
On va obtenir quelque chose comme  \large e^{-\frac{\beta}{2\,\alpha}\,t}
La constante de temps est donc  \large \frac{2\,\alpha}{\beta}
Et ici on trouve pour la constante de temps
\large \tau\,=\,\frac{2RLC}{L+RrC}  qui a bien la dimension d'un temps   ( sauf erreur de ma part )
Quant à la pseudo-période, ce n'est pas  2\pi\sqrt{LC}  qui est la période propre mais
\omega\,=\,\sqrt{-\Delta}  avec  \Delta\,<\,0 bien sûr

Posté par
Marc35re : Exercice sur un circuit RLC 02-12-12 à 15:30

Donc
\large T\,=\,\frac{2\pi}{\omega}\,=\,\frac{2\pi}{\sqrt{-\Delta}}

Posté par
Marc35re : Exercice sur un circuit RLC 02-12-12 à 15:33

Non...erreur... Je commençais à fatiguer sans doute...
\large \omega\,=\,\frac{\sqrt{-\Delta}}{2\alpha}  avec  \Delta\,<\,0 bien sûr
Donc
\Large T\,=\,\frac{2\pi}{\omega}\,=\,\frac{2\pi}{\frac{\sqrt{-\Delta}}{2\alpha}}

Posté par
Marc_Benfordre : Exercice sur un circuit RLC 02-12-12 à 17:29

Whaou, c'est pas du tout ce que j'ai essayé de faire.
J'avais essayé d'exprimer la valeur de r qui annulerait le discriminant Delta de l'équation homogène sans second membre associée à l'équation différentielle :
\\ LC \frac{d^2Vs}{dt^2} + \frac{L + rRC}{R} \frac{dVs}{dt} + \frac{r + R}{R} Vs = E \\ LC x^2 + \frac{L + rRC}{R} x + \frac{r + R}{R} = 0 \\ Delta = b^2 – 4ac = 0 \\ \frac{L + rRC}{R}^2 – 4LC \frac{r + R}{R} = 0 \\ \frac{L^2 + 2rRLC + r^2R^2C^2 – 4rRLC – 4R^2LC}{R^2} = 0 \\ L^2 + 2rRLC + r^2R^2C^2 – 4rRLC – 4R^2LC = 0 \\ R^2C^2r^2 – 2RLCr + L^2 – 4R^2LC = 0
On obtient un nouveau polynôme qu'il faut résoudre :
Delta = b^2 – 4ac \\ Delta = 16R^4LC^3
Et les deux solutions sont donc :
r(critique) = \frac{L}{RC} + 2 \sqrt{\frac{L}{C}} \\ r(critique) = \frac{L}{RC} - 2 \sqrt{\frac{L}{C}} \\


Mais d'après ce que tu me dis, il faut en faite juste faire ça :
\\ LC \frac{d^2Vs}{dt^2} + \frac{L + rRC}{R} \frac{dVs}{dt} + \frac{r + R}{R} Vs = E \\ LC x^2 + \frac{L + rRC}{R} x + \frac{r + R}{R} = 0 \\ Delta = 0 \\ r(critique) = - \frac{b}{2a} \\ r(critique) = - \frac{L + rRC}{2RLC} \\ Puis : \\ Tau = \frac{2a}{b} \\ Tau = \frac{2RLC}{L + rRC} \\

C'est bien ça ?


Mais par contre ce qui me paraît bizarre c'est qu'ensuite avec ton expression de \Large T\,=\,\frac{2\pi}{\omega}\,=\,\frac{2\pi}{\frac{\sqrt{-\Delta}}{2\alpha}} bah ça va pas faire très joli je crois vu que le Delta ne s'exprime pas très simplement vu que Delta = \frac{L^2 + 2rRLC + r^2R^2C^2 – 4rRLC – 4R^2LC}{R^2}

Edit Coll : image remplacée par l'expression Latex

Posté par
Marc_Benfordre : Exercice sur un circuit RLC 02-12-12 à 19:46

Euh apparemment le latex de mon message a buggé (pourtant quand j'ai validé mon message la première fois tout étais bien mais bon).
Par chance j'ai sauvegardé mon message alors je le remets (j'ai pas trouvé où était le bouton "éditer" s'il y en a un ici alors désolé) :

____


Whaou, c'est pas du tout ce que j'ai essayé de faire.
J'avais essayé d'exprimer la valeur de r qui annulerait le discriminant Delta de l'équation homogène sans second membre associée à l'équation différentielle :
LC \frac{d^2Vs}{dt^2} + \frac{L + rRC}{R} \frac{dVs}{dt} + \frac{r + R}{R} Vs = E \\ LC x^2 + \frac{L + rRC}{R} x + \frac{r + R}{R} = 0 \\ Delta = b^2 - 4ac = 0 \\ \frac{L + rRC}{R}^2 - 4LC \frac{r + R}{R} = 0 \\ \frac{L^2 + 2rRLC + r^2R^2C^2 - 4rRLC - 4R^2LC}{R^2} = 0 \\ L^2 + 2rRLC + r^2R^2C^2 - 4rRLC - 4R^2LC = 0 \\ R^2C^2r^2 - 2RLCr + L^2 - 4R^2LC = 0
On obtient un nouveau polynôme qu'il faut résoudre :
Delta = b^2 - 4ac \\ Delta = 16R^4LC^3
Et les deux solutions sont donc :
r(critique) = \frac{L}{RC} + 2 \sqrt{\frac{L}{C}}
et r(critique) = \frac{L}{RC} - 2 \sqrt{\frac{L}{C}}


Mais d'après ce que tu me dis, il faut en faite juste faire ça :
\\ LC \frac{d^2Vs}{dt^2} + \frac{L + rRC}{R} \frac{dVs}{dt} + \frac{r + R}{R} Vs = E \\ LC x^2 + \frac{L + rRC}{R} x + \frac{r + R}{R} = 0 \\ Delta = 0 \\ r(critique) = - \frac{b}{2a} \\ r(critique) = - \frac{L + rRC}{2RLC}
Puis :
Tau = \frac{2a}{b} \\ Tau = \frac{2RLC}{L + rRC}

C'est bien ça ?


Mais par contre ce qui me paraît bizarre c'est qu'ensuite avec ton expression de T = \frac{2pi}{omega} = \frac{2pi}{\frac{\sqrt{-\Delta}}{2alpha}} bah ça va pas faire très joli je crois vu que le Delta ne s'exprime pas très simplement vu que Delta = \frac{L^2 + 2rRLC + r^2R^2C^2 - 4rRLC - 4R^2LC}{R^2}


____


Normalement y'aura pas de "Erreur de Latex" cette fois-ci.

Posté par
Marc35re : Exercice sur un circuit RLC 02-12-12 à 20:02

Non pour la résistance critique... Ce n'est pas ce que j'ai dit...
Les valeurs que tu as calculées avant, étaient bonnes bien qu'il y ait 2 valeurs et que ça me paraît bizarre a priori...
On a :
\Delta\,=\,\left(\frac{L}{R}\,-\,r\,C\right)^2\,-\,4\,L\,C
Et la rcritique est calculée avec  \Delta\,=\,0.
Donc :
r_{critique}\,=\,\frac{L}{RC}\,\pm\,2\,\sqrt{\frac{L}{C}}

Posté par
Marc35re : Exercice sur un circuit RLC 02-12-12 à 20:31

Je ne sais pas si ça ne va pas être joli mais il y a peut-être moyen de l'écrire autrement...
Dans le cas \Delta\,<\,0, on a :

\large x\,=\,\frac{-\left(\frac{L}{R}+rC\right)\,\pm\,j\sqrt{-\Delta}}{2LC}

\large x\,=\,\frac{-\left(\frac{L}{R}+rC\right)}{2LC}\,\pm\,j\frac{\sqrt{-\Delta}}{2LC}
Que l'on peut écrire :
\Large x\,=\,\frac{1}{\tau}\,\pm\,j\omega
\tau est la valeur que j'ai donnée précédemment  \large \tau\,=\,\frac{2RLC}{L+RrC}, valeur avec laquelle tu sembles être d'accord...
\Large \omega\,=\,\frac{\sqrt{-\Delta}}{2LC}\,=\,\frac{\sqrt{4LC\,-\,\left(\frac{L}{R}}-rC\right)^2}{2LC}

\Large \omega\,=\,\frac{2\sqrt{LC}\,\sqrt{1\,-\,\left(\frac{L}{R}}-rC\right)^2\,\frac{1}{4LC}}{2LC}

\Large \omega\,=\,\frac{1}{\sqrt{LC}}\,\left(\sqrt{1\,-\,\left(\frac{L}{R}}-rC\right)^2\,\frac{1}{4LC}\,\right)
Il est intéressant de l'écrire de cette façon parce qu'on fait apparaître la pulsation propre  \frac{1}{\sqrt{LC}} avec un terme correctif (certes pas très simple).
On peut visualiser plus facilement l'écart par rapport à la pulsation propre et quels sont les termes qui interviennent.
Donc la période est   \large T\,=\,\frac{2\,\pi}{\omega}

\Large T\,=\,2\pi\sqrt{LC}\,\frac{1}{\sqrt{1\,-\,\left(\frac{L}{R}}-rC\right)^2\,\frac{1}{4LC}}

Posté par
Marc35re : Exercice sur un circuit RLC 02-12-12 à 20:42

On peut voir d'ailleurs que, si  R\,\rightarrow\,+\infty  et   r\,=\,0 , on retrouve la période propre. Cela est normal parce qu'on a alors un circuit LC série.

Posté par
Marc_Benfordre : Exercice sur un circuit RLC 02-12-12 à 21:58

Je suis presque d'accord avec tout tes calculs, sauf pour la valeur de Delta.
L'équation différentielle étant : LC \frac{d^2Vs}{dt^2} + \frac{L + rRC}{R} \frac{dVs}{dt} + \frac{r + R}{R} Vs = E
On a :
LC x^2 + \frac{L + rRC}{R} x + \frac{r + R}{R} = 0
Delta = b^2 - 4ac
Delta = \frac{L + rRC}{R}^2 - 4LC\frac{r + R}{R}
Delta = \frac{L^2 + r^2R^2C^2 + 2rRLC - 4rRLC - 4R^2LC}{R^2}
Delta = \frac{L^2 + r^2R^2C^2 - 2rRLC - 4R^2LC}{R^2}

Et pour le fait qu'il y ai deux valeurs pour la résistance critique, peut-être que c'est à cause qu'il y à une erreur dans l'équation différentielle (mais je vois pas où), ou bien c'est peut-être parce qu'il faut ensuite éliminer une des deux valeurs : en effet, ils nous donnent les valeurs de R, L et C, et une des deux valeurs de la résistance critique est négative..

Posté par
Marc_Benfordre : Exercice sur un circuit RLC 02-12-12 à 22:17

Euh.. avec mon Delta on trouve :
Omega = \frac{\sqrt{4R^2LC + 2rRLC - L^2 - r^2R^2C^2}}{2RLC}
Ce qui est terriblement moche... ça ne peut clairement pas être ça.

Posté par
Marc_Benfordre : Exercice sur un circuit RLC 02-12-12 à 22:47

J'ai revérifié tout les calculs et je vois vraiment pas d'où viennent les bizarreries (ou peut-être que c'est dès le début que j'ai faux, au commencement de l'établissement de l'équation différentielle...).
Par contre après avoir fait les applications numériques on trouve du 0,06s pour la pseudo-période et du 20ohm pour la résistance critique ce qui a l'air plausible.

Posté par
Marc35re : Exercice sur un circuit RLC 02-12-12 à 23:36

\large \Delta\,=\,\left(\frac{L}{R}+rC\right)^2\,-\,4\,L\,C\,\frac{r+R}{R}

\large \Delta\,=\,\frac{L^2}{R^2}\,+\,r^2C^2\,+\,2\frac{LRrC}{R^2}\,-\,4\,L\,C\,\frac{r}{R}\,-\,4\,L\,C

\large \Delta\,=\,\frac{L^2}{R^2}\,+\,r^2C^2\,+\,2\frac{LrC}{R}\,-\,4\,\frac{L\,r\,C}{R}\,-\,4\,L\,C

\large \Delta\,=\,\frac{L^2}{R^2}\,+\,r^2C^2\,-\,2\,\frac{L\,r\,C}{R}\,-\,4\,L\,C

\large \Delta\,=\,\left(\frac{L}{R}-rC\right)^2\,-\,4\,L\,C

Posté par
Marc35re : Exercice sur un circuit RLC 02-12-12 à 23:38

Je vais vérifier l'équation différentielle au cas où...
Mais efpe l'a déjà vérifiée.

Posté par
Marc35re : Exercice sur un circuit RLC 03-12-12 à 11:52

Comme je le pensais, l'équation est bonne.
Pour avoir \Delta\,\le\,0 , on a :

\large \frac{L}{RC}\,-\,2\sqrt{\frac{L}{C}}\,\le\,r\,\le\,\frac{L}{RC}\,+\,2\sqrt{\frac{L}{C}}
si   \normalsize \frac{L}{RC}\,-\,2\sqrt{\frac{L}{C}}\,>\,0\,\Rightarrow\,R\,\le\,\frac{1}{2}\,\sqrt{\frac{L}{C}}
sinon
\large 0\,\le\,r\,\le\,\frac{L}{RC}\,+\,2\sqrt{\frac{L}{C}}     (une résistance est toujours positive ou nulle)
Donc, selon les valeurs, on peut avoir 2 valeurs pour la résistance critique... ce qui me "chiffonne" un peu...
Quelles sont les valeurs des composants ?

En LaTeX, pour écrire \Delta, il faut écrire \Delta  (et \delta pour \delta).
Même chose pour \omega, il faut écrire \omega

Posté par
Marc35re : Exercice sur un circuit RLC 03-12-12 à 11:53

Faut-il calculer la solution de l'équation différentielle ?

Posté par
Marc_Benfordre : Exercice sur un circuit RLC 04-12-12 à 01:02

Ah d'accord, je comprends maintenant ta valeur de \Delta.

Pour les deux valeurs de la résistance critique, on trouve 20 \Omega. Comme une des valeurs est négative on l'élimine j'imagine, donc tout va bien.

Et d'accord pour le Latex. J'avais essayé d'écrire \Delta en cliquant sur le ("insérer un symbole mathématiques") en bas de la boite de rédaction de message, et ça faisait chaque fois tout bugger tout le reste du Latex (bizarrement maintenant ça a l'air de marcher).

Et quant à calculer la solution de l'équation différentielle, heureusement non, ça n'est pas demandé.

Bref, un grand merci pour toute l'aide que tu m'as apporté !

Posté par
Marc35re : Exercice sur un circuit RLC 04-12-12 à 10:47

Citation :
Pour les deux valeurs de la résistance critique, on trouve \pm\,20\,\Omega. Comme une des valeurs est négative on l'élimine j'imagine,

Certes, on élimine la valeur négative... Avoir une valeur négative, c'est ce qui pouvait arriver de mieux !
Quant à l'équation différentielle, elle n'est pas si difficile à résoudre...


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !