Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Equa diff d'un circuit bouchon

Posté par
confiture96 09-02-16 à 14:47

Bonjour,

Je bloque sur un exercice. Le but est de déterminer l'équation differentielle caractérisant ce circuit de type bouchon grâce à la loi des mailles et des n?uds..
Mon problème est que mes i traversant le circuits sont different et jai alors 3 inconnues...
Merci d'avance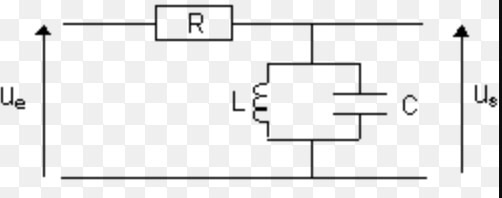

Equa diff d\'un circuit bouchon

Posté par
vanoisere : Equa diff d'un curcuit bouchon 09-02-16 à 15:07

Bonjour
En orientant tous les dipôles en conventions récepteur : i à travers R orientée positivement vers la droite, iL et iC orientées positivement vers le bas sur ton schéma, on obtient, sachant que le symbole   désigne une primitive :

i_{C}(t)=C\frac{du(t)}{dt}\quad;\quad u(t)=L\frac{di_{L}}{dt}\quad donc\quad i_{L}(t)=\frac{1}{L}\intop u(t).dt \\ \\   \\ \\ \text{loi des noeuds :\ensuremath{i(t)=i_{C}(t)+i_{L}(t)=C\frac{du(t)}{dt}+\frac{1}{L}\intop u(t).dt}} \\ \\   \\ \\ \text{en multipliant tous les termes par L et en dérivant par rapport à t pour faire disparaitre la primitive :} \\ \\   \\ \\ \boxed{u(t)+LC\frac{d^{2}u(t)}{dt^{2}}=\frac{L.di(t)}{dt}}
Tu peux vérifer que cette équation différentielle correspond bien aux expressions classiques des impédances en régime sinusoïdal établi :
Sachant que dérivée n fois une grandeur instantanée fonction sinusoïdale du temps  est équivalent à multiplier par (j)n le complexe associé à cette grandeur sinusoïdale, l'équation différentielle précédente conduit à :

\underline{u}\left(1+LC\left(j\omega\right)^{2}\right)=jL\omega\underline{i} \\ \\   \\ \\ \text{d'où l'expression de l'impédance complexe : \ensuremath{\underline{Z}=\frac{\underline{u}}{\underline{i}}=\frac{jL\omega}{1-LC\omega^{2}}}} \\ \\  
Bien sûr, on obtient le même résultat en appliquant la "formule" de l'impédance équivalente à deux dipôles associés en parallèle :

\underline{Z}=\frac{\underline{Z_{L}}\cdot\underline{Z_{C}}}{\underline{Z_{L}}+\underline{Z_{C}}}=\frac{jL\omega\cdot\frac{1}{jC\omega}}{jL\omega+\frac{1}{jC\omega}}=\frac{\frac{L}{C}}{j\left(L\omega-\frac{1}{C\omega}\right)} \\ \\   \\ \\ \text{soit en multipliant tous les termes par \ensuremath{jC\omega\::\:\boxed{\underline{Z}=\frac{jL\omega}{1-LC\omega^{2}}}}} \\ \\  

Posté par
J-Pre : Equa diff d'un curcuit bouchon 09-02-16 à 15:58

Méthode 1

Z(L//C) = (jwL/(jwC))/(jwL + 1/(jwC)) = jwL/(1 + j²w²LC)

Ue/(R+Z) = Us/Z

Us/Ue = Z/(R+Z) = [jwL/(1 + j²w²LC)]/[R + jwL/(1 + j²w²LC)]

Us/Ue = Z/(R+Z) = jwL/(R + j²w²LCR + jwL)

(R + jwL + j²w²LCR) Us = jwL.Ue

Et en remplaçant jw par d/dt --->

R.Us + L.dUs/dt + LCR d²Us/dt² = L.dUe/dt

d²Us/dt² + (1/(RC)).dUs/dt + 1/(LC).Us = (1/(RC)).dUe/dt
-----
Autrement.

Méthode 2 (loi des mailles et loi des noeuds) :

Ue = R.i + Us
Us = L.diL/dt
ic = C.dUc/dt
i = ic + iL

On élimine i :
Ue = R.(ic + iL) + Us --> dUe/dt = R.dic/dt + R.diL/dt + dUs/dt
Us = L.diL/dt
ic = C.dUc/dt

On élimine iL
dUe/dt = R.dic/dt + (R/L).Us + dUs/dt
ic = C.dUc/dt --> dic/dt = C.d²Us/dt²

On élimine ic :

dUe/dt = R.C.d²Us/dt² + (R/L).Us + dUs/dt

R.C.d²Us/dt² + dUs/dt + (R/L).Us = dUe/dt

d²Us/dt² + (1/(RC)).dUs/dt + (1/(LC)).Us = (1/(RC)).dUe/dt
-----
Sauf distraction.  

Posté par
vanoisere : Equa diff d'un curcuit bouchon 09-02-16 à 17:06

J'ai effectivement posté un peu vite en envoyant un copier-collé d'un sujet analogue récent... Ce que j'ai écrit concerne us et non u.
Je rectifie :

i_{C}(t)=C\frac{du_s(t)}{dt}\quad;\quad u_s(t)=L\frac{di_{L}}{dt}\quad donc\quad i_{L}(t)=\frac{1}{L}\intop u_s(t).dt \\ \\  \\ \text{loi des noeuds :\ensuremath{i(t)=i_{C}(t)+i_{L}(t)=C\frac{du_s(t)}{dt}+\frac{1}{L}\intop u_s(t).dt}} \\ \\  \\ \text{en multipliant tous les termes par L et en dérivant par rapport à t pour faire disparaitre la primitive :} \\ \\  \\ \boxed{u_s(t)+LC\frac{d^{2}u_s(t)}{dt^{2}}=\frac{L.di(t)}{dt}}
Puisque :

i(t)=\frac{u(t)-u_{s}(t)}{R}\quad;\quad L\frac{di(t)}{dt}=\frac{L}{R}\frac{du(t)}{dt}-\frac{L}{R}\frac{du_{s}(t)}{dt}
On obtient au final :

LC\frac{du_{s}^{2}(t)}{dt^{2}}+\frac{L}{R}\frac{du_{s}(t)}{dt}+u_{s}(t)=\frac{L}{R}\frac{du(t)}{dt}
Soit, après divisisions par LC :

\boxed{\frac{du_{s}^{2}(t)}{dt^{2}}+\frac{1}{RC}\cdot\frac{du_{s}(t)}{dt}+\frac{1}{LC}\cdot u_{s}(t)=\frac{1}{RC}\cdot\frac{du(t)}{dt}}
Résultat obtenu par JP par une méthode différente. On peut vérifier l'homogénéité du résultat sachant que RC a la dimension d'un temps et LC la dimension d'un temps au carré.
Je présente mes excuses pour mon premier message mal adapté à la question posée.

Posté par
confiture96re : Equa diff d'un curcuit bouchon 09-02-16 à 19:38

ne manque t il pas un - quelque part?
En effet je lis dans mon cours que l'equa diff et toujours de la mm forme avec e(t)= LC d2uc/dt2 + RCDuc/dt + uc(t)

Posté par
confiture96re : Equa diff d'un curcuit bouchon 09-02-16 à 19:52

es-ce parce que dans mon enoncé exacte on a un générateur qui induit une e(t) ?

Posté par
vanoisere : Equa diff d'un curcuit bouchon 10-02-16 à 00:20

Si les deux bornes d'entrée (bornes de gauche) sont reliées à un générateur idéal de tension de force-électromotrice e(t) il suffit de poser ue(t)=u(t) =e(t) :

\boxed{\frac{du_{s}^{2}(t)}{dt^{2}}+\frac{1}{RC}\cdot\frac{du_{s}(t)}{dt}+\frac{1}{LC}\cdot u_{s}(t)=\frac{1}{RC}\cdot\frac{de(t)}{dt}}

Posté par
J-Pre : Equa diff d'un curcuit bouchon 10-02-16 à 09:11

Noter \frac{d^2u_{s}(t)}{dt^{2}} au lieu de \frac{du_{s}^{2}(t)}{dt^{2}}

Posté par
vanoisere : Equa diff d'un curcuit bouchon 10-02-16 à 11:38


Bonjour
Merci JP : il s'agit bien d'une dérivée seconde. Je ne suis pas encore totalement à l'aise avec Tex...

Posté par
confiture96re : Equa diff d'un curcuit bouchon 10-02-16 à 17:52

merci beaucoup j'ai compris!
si mon Il(0= E/R comment déterminer du(o)/dt je trouve que c'est = à 0 mais c'est pas cohérent.. je ne vois pas ou je me suis trompée

Posté par
confiture96re : Equa diff d'un curcuit bouchon 10-02-16 à 17:53

IL(t=0)=E/R *

Posté par
vanoisere : Equa diff d'un curcuit bouchon 10-02-16 à 18:56

Bonjour,
Tu n'as pas posté l'intégralité de l'énoncé, ce qui complique un peu l'aide. On suppose qu'avant l'établissement de la tension E, le condensateur est déchargé et qu'aucun courant ne circule.
Continuité de iL en t = 0 : iL(0+)=0 ;
continuité de la tension aux bornes du condensateur : us(0+)=0
Loi d'Ohm : i(0+) = (E - us(0+))/R = E/R
loi des nœuds : i(0+) = iL(0+) + iC(O+) donc iC(0+) = E/R)
Sous réserve d'avoir bien "deviné" l'énoncé...

Posté par
confiture96re : Equa diff d'un circuit bouchon 11-02-16 à 20:44

Merci beaucoup à vous deux pour vos réponses


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2024

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !